M8 Inverse of a 2x2 matrix
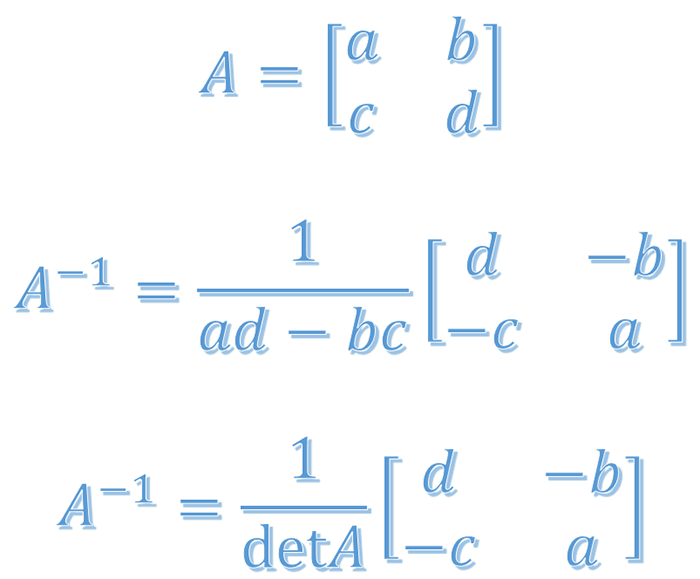
In matrix algebra, we can add, subtract and multiply matrices subject to conditions on the matrix shape (or order). While matrix algebra does not have a division operation, there is multiplication by the inverse matrix. This module discuses the concept of an inverse matrix.
Definition
Let \(I\) denote the identity matrix. That is the matrix containing ones on the main diagonal and zeros elsewhere. That is \[\begin{align*} I_{1}=\left[1\right],\;I_{2} & =\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right],\;I_{3}=\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right],\;I_{4}=\left[\begin{array}{cccc} 1 & 0 & 0 & 0\\ 0 & 1 & 0 & 0\\ 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 1 \end{array}\right],\;I_{n}=\left[\begin{array}{ccccc} 1 & 0 & 0 & \cdots & 0\\ 0 & 1 & 0 & \cdots & 0\\ 0 & 0 & 1 & \cdots & 0\\ \vdots & \vdots & \vdots & \ddots & \vdots\\ 0 & 0 & 0 & \cdots & 1 \end{array}\right]. \end{align*}\]
If \(A\) is a square matrix and \(B\) is another square matrix of the same order such that \[\begin{align*} AB & =BA=I \end{align*}\] then we call \(B\) the inverse of \(A.\) The inverse of \(A\) is denoted by the symbol \(A^{-1}\).1 Note that \[\begin{align*} A^{-1} & \neq\frac{1}{A} \end{align*}\] as division is not defined in matrix algebra. Hence \[\begin{align*} AA^{-1} & =A^{-1}A=I. \end{align*}\]
Not every square matrix has an inverse. If the determinant of a matrix equals zero, the inverse does not exist and the matrix is called singular. If the determinant is unequal to zero the inverse exists and we call the matrix non-singular or invertible.
Inverse of a \(2\times2\) Matrix
If \(A\) is a \(2\times2\) matrix, then \(A^{-1}\) is also a \(2\times2\) matrix such that: \[\begin{align*} AA^{-1} & =A^{-1}A=\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]. \end{align*}\] There is a simple formula to find the matrix of a \(2\times2\) matrix.
Let \[\begin{align*} A=\left[\begin{array}{cc} a & b\\ c & d \end{array}\right] \end{align*}\] then the inverse matrix of \(A\) is given by \[\begin{align*} A^{-1} & =\frac{1}{ad-bc}\left[\begin{array}{cc} d & -b\\ -c & a \end{array}\right]. \end{align*}\]
Note that \(ad-bc\) is the determinant of the matrix \(A.\) That is \(ad-bc=\det A=\left|A\right|\). So we can also write \[\begin{align*} A^{-1} & =\frac{1}{\det A}\left[\begin{array}{cc} d & -b\\ -c & a \end{array}\right]. \end{align*}\] If \(\det A=0,\) we have \[\begin{align*} A^{-1} & =\frac{1}{0}\left[\begin{array}{cc} d & -b\\ -c & a \end{array}\right]. \end{align*}\] But \(1/0\) is undefined and so the inverse does not exist.
Example 1
Find the inverse of the matrix \(A=\left[\begin{array}{cc} 2 & 3\\ 2 & 4 \end{array}\right]\).
Solution:
First check if \(A\) is singular. \[\begin{align*} \det A & =2\times4-2\times3\\ & =8-6\\ & =2 \end{align*}\] so \(A\) is not singular and the inverse exists. Using the formula above, \[\begin{align*} A^{-1} & =\frac{1}{\det A}\left[\begin{array}{cc} 4 & -3\\ -2 & 2 \end{array}\right]\\ & =\frac{1}{2}\left[\begin{array}{cc} 4 & -3\\ -2 & 2 \end{array}\right]\\ & =\left[\begin{array}{cc} 2 & -3/2\\ -1 & 1 \end{array}\right] \end{align*}\] Check \(AA^{-1}=I\) and \(A^{-1}A=I.\) \[\begin{align*} AA^{-1} & =\left[\begin{array}{cc} 2 & 3\\ 2 & 4 \end{array}\right]\left[\begin{array}{cc} 2 & -3/2\\ -1 & 1 \end{array}\right]\\ & =\left[\begin{array}{cc} 2\times2+3\times\left(-1\right) & 2\times\left(-3/2\right)+3\times1\\ 2\times2+4\times\left(-1\right) & 2\times\left(-3/2\right)+4\times1 \end{array}\right]\\ & =\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]\\ A^{-1}A & =\left[\begin{array}{cc} 2 & -3/2\\ -1 & 1 \end{array}\right]\left[\begin{array}{cc} 2 & 3\\ 2 & 4 \end{array}\right]\\ & =\left[\begin{array}{cc} 2\times2+\left(-3/2\right)\times2 & 2\times3+\left(-3/2\right)\times4\\ -1\times2+1\times2 & \left(-1\right)\times3+1\times4 \end{array}\right]\\ & =\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]. \end{align*}\] So \(A^{-1}=\left[\begin{array}{cc} 2 & -3/2\\ -1 & 1 \end{array}\right]\) is the inverse of \(A.\)
Example 2
Find the inverse of the matrix \(A=\left[\begin{array}{cc} -1 & -2\\ 4 & 3 \end{array}\right]\).
Solution:
The determinant, \[\begin{align*} \det A & =-1\times3-\left(-2\right)\times4\\ & =-3-\left(-8\right)\\ & =5 \end{align*}\] so the matrix \(A\) has an inverse. Using the formula, \[\begin{align*} A^{-1} & =\frac{1}{\det A}\left[\begin{array}{cc} 3 & 2\\ -4 & -1 \end{array}\right]\\ & =\frac{1}{5}\left[\begin{array}{cc} 3 & 2\\ -4 & -1 \end{array}\right]. \end{align*}\] Check \(AA^{-1}=I\) and \(A^{-1}A=I.\) \[\begin{align*} AA^{-1} & =\left[\begin{array}{cc} -1 & -2\\ 4 & 3 \end{array}\right]\left(\frac{1}{5}\left[\begin{array}{cc} 3 & 2\\ -4 & -1 \end{array}\right]\right)\\ & =\frac{1}{5}\left[\begin{array}{cc} -1 & -2\\ 4 & 3 \end{array}\right]\left[\begin{array}{cc} 3 & 2\\ -4 & -1 \end{array}\right]\\ & =\frac{1}{5}\left[\begin{array}{cc} -3+8 & -2+2\\ 12-12 & 8-3 \end{array}\right]\\ & =\frac{1}{5}\left[\begin{array}{cc} 5 & 0\\ 0 & 5 \end{array}\right]\\ & =\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]\\ A^{-1}A & =\frac{1}{5}\left[\begin{array}{cc} 3 & 2\\ -4 & -1 \end{array}\right]\left[\begin{array}{cc} -1 & -2\\ 4 & 3 \end{array}\right]\\ & =\frac{1}{5}\left[\begin{array}{cc} -3+8 & -6+6\\ 4-4 & 8-3 \end{array}\right]\\ & =\frac{1}{5}\left[\begin{array}{cc} 5 & 0\\ 0 & 5 \end{array}\right]\\ & =\left[\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right]. \end{align*}\] So \(A^{-1}=\frac{1}{5}\left[\begin{array}{cc} 3 & 2\\ -4 & -1 \end{array}\right].\)
Example 3
Find the inverse of the matrix \(A=\left[\begin{array}{cc} 3 & 2\\ 6 & 4 \end{array}\right].\)
Solution: The determinant of \(A\) is \[\begin{align*} \det A & =3\times4-6\times2\\ & =12-12\\ & =0. \end{align*}\] Since \(\det A=0,\)the matrix \(A\) does not have an inverse.
Exercise 1
Find if possible, the inverses of the following matrices:
\[\begin{align*} a)\, & \left[\begin{array}{cc} 2 & -1\\ -4 & 3 \end{array}\right] & b) & \left[\begin{array}{cc} 0 & 4\\ 2 & 5 \end{array}\right] & c) & \left[\begin{array}{cc} -2 & -3\\ 6 & 9 \end{array}\right] & d) & \left[\begin{array}{cc} -3 & 4\\ 2 & 1 \end{array}\right]. \end{align*}\]
\[\begin{align*} \begin{array}{llll} a)\,\left[\begin{array}{cc} 3/2 & 1/2\\ 2 & 1 \end{array}\right] & b)\,\left[\begin{array}{cc} -5/8 & 1/2\\ 1/4 & 0 \end{array}\right] & c)\,\textrm{Inverse does not exist} & d)\,\frac{1}{11}\left[\begin{array}{cc} -1 & 4\\ 2 & 3 \end{array}\right].\end{array} \end{align*}\]
Exercise 2
For
\[\begin{align*} A & =\left[\begin{array}{cc} -1 & -3\\ 2 & 5 \end{array}\right]\textrm{ and $B=\left[\begin{array}{cc} -2 & 0\\ 4 & 1 \end{array}\right]$ } \end{align*}\] find \(A^{-1}\) and \(B^{-1}\) and show that \(\left(AB\right)^{-1}=B^{-1}A^{-1}.\)
\[\begin{align*} A^{-1} & =\left[\begin{array}{cc} 5 & 3\\ -2 & -1 \end{array}\right],\quad B^{-1}=\left[\begin{array}{cc} -1/2 & 0\\ 2 & 1 \end{array}\right]. \end{align*}\]
Download this page, M8 Inverse of a 2x2 matrix (PDF 160KB)
What's next... M9 Inverse of a 3x3 matrix
