M6 Systems of equations
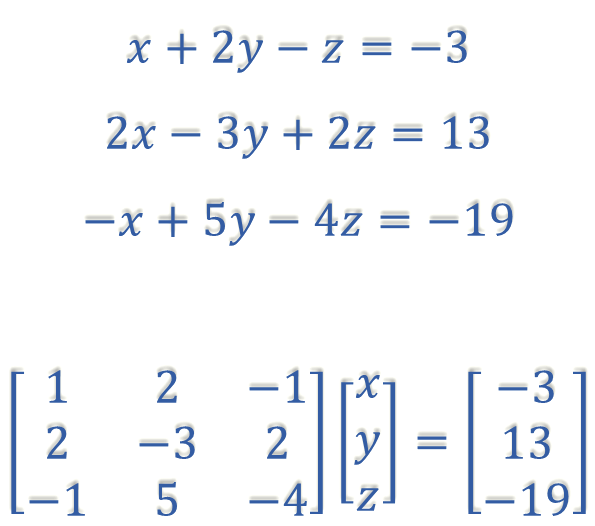
Matrices can be used to solve systems of equations by using elementary row operations and the augmented matrix. This module discusses these topics.
The Augmented Matrix
Consider the following system of equations: \[\begin{align*} x+2y-z & =-3\\ 2x-3y+2z & =13\\ -x+5y-4z & =-19 \end{align*}\] The corresponding augmented matrix for this system is \[\begin{align*} \left[\begin{array}{ccc} 1 & 2 & -1\\ 2 & -3 & 2\\ -1 & 5 & -4 \end{array}\left|\begin{array}{c} -3\\ 13\\ -19 \end{array}\right.\right]. \end{align*}\]
The first row comprises the three coefficients of \(x,y\) and \(z\,\left(1,2,-1\right)\) and the right hand side \(\left(-3\right)\) from the first equation.
The second row comprises the three coefficients of \(x,y\) and \(z\,\left(2,-3,2\right)\) and the right hand side \(\left(13\right)\) from the second equation.
The third row comprises the three coefficients of \(x,y\) and \(z\,\left(-1,4,-4\right)\) and the right hand side \(\left(-19\right)\) from the third equation.
The vertical line indicates this is an augmented matrix and should be included. Otherwise it would look like a \(3\times4\) matrix.
Elementary Row Operations
Elementary row operations are operations that can be used to simplify an augmented matrix when solving systems of equations. Allowable elementary row operations are:
Interchange any two rows.
Multiply a row by any constant.
Add or subtract a multiple of one row to another row.
Solving Equations
The method is as follows:
Create the augmented matrix
Use row operations to reduce the augmented matrix to the following form
1Note that you must get the zeros under the diagonal elements by working from left to right.
\[\begin{align*} \left[\begin{array}{ccc} a & b & c\\ 0 & e & f\\ 0 & 0 & h \end{array}\left|\begin{array}{c} d\\ g\\ k \end{array}\right.\right]. \end{align*}\] Note that the entries below the main diagonal are zero.
From row \(3\) we have \(hz=k\) and so \(z=k/h.\)
From row \(2\) we have \(ey+fz=g.\) Since \(z\) is known (from Step 3), this can be arranged to find \(y.\)
From row \(1\) we have \(ax+by+cz=d.\) Since \(x\) and \(y\) are known from steps \(3\) and \(4\) we can find \(x.\)
Steps \(3\) to \(5\) are called back substitution.
Example 1
Solve the following for \(x,\,y\) and \(z:\) \[\begin{align*} x+2y-z & =-3 & \left(1\right)\\ 2x-3y+2z & =13 & \left(2\right)\\ -x+5y-4z & =-19. & \left(3\right) \end{align*}\]
Solution: The augmented matrix is: \[\begin{align*} \left[\begin{array}{ccc} 1 & 2 & -1\\ 2 & -3 & 2\\ -1 & 5 & -4 \end{array}\left|\begin{array}{c} -3\\ 13\\ -19 \end{array}\right.\right]. \end{align*}\] We now use row operations to get zeroes in row \(2\) and row \(3\) of column \(1\). We do this by multiplying row \(1\) \(\left(R_{1}\right)\) by 2 and subtracting it from row \(2\) \(\left(R_{2}\right)\) to get:2 We will work from left to right.
\[\begin{align*} \begin{array}{c} \\ R_{2}'=R_{2}-2R_{1}\\ \\ \end{array}\left[\begin{array}{ccc} 1 & 2 & -1\\ 0 & -7 & 4\\ -1 & 5 & -4 \end{array}\left|\begin{array}{c} -3\\ 19\\ -19 \end{array}\right.\right]. \end{align*}\]
Now, to get a zero in row \(3\) column \(1,\) we add rows \(1\) and 3 to get: \[\begin{align*} \begin{array}{c} \\ \\ R_{3}'=R_{3}+R_{1} \end{array}\left[\begin{array}{ccc} 1 & 2 & -1\\ 0 & -7 & 4\\ 0 & 7 & -5 \end{array}\left|\begin{array}{c} -3\\ 19\\ -22 \end{array}\right.\right]. \end{align*}\] Next we get a zero in row \(3\), column \(1\) by adding rows \(2\) and \(3:\) \[\begin{align*} \begin{array}{c} \\ \\ R_{3}'=R_{3}+R_{2} \end{array}\left[\begin{array}{ccc} 1 & 2 & -1\\ 0 & -7 & 4\\ 0 & 0 & -1 \end{array}\left|\begin{array}{c} -3\\ 19\\ -3 \end{array}\right.\right]. \end{align*}\] Now we can start the back substitution. From row \(3\) we have \(-1z=-3\) so \(z=3.\) From row \(2\) we have \(-7y+4z=19\). Substituting for \(z\) we get \[\begin{align*} -7y+4z & =19\\ -7y+4\left(3\right) & =19\\ -7y & =7\\ y & =-1. \end{align*}\] From row \(1\) we have \(x+2y-z=-3\). Substituting for \(y\) and \(z\) gives \[\begin{align*} x+2y-z & =-3\\ x+2\left(-1\right)-3 & =-3\\ x-5 & =-3\\ x & =2. \end{align*}\] The solution to the simultaneous equations is therefore, \(x=2,\,y=-1,\,z=3\).
Note that you can check your solution by substituting the values for \(x,y\) and \(z\) in the original equations.
For example the left hand side of equation \(\left(1\right)\) is \[\begin{align*} x+2y-z & =2+2\left(-1\right)-3\\ & =2-2-3\\ & =-3\\ & =RHS. \end{align*}\] The left hand side of equation \(\left(2\right)\) is \[\begin{align*} 2x-3y+2z & =2(2)-3\left(-1\right)+2\left(3\right)\\ & =4+3+6\\ & =13\\ & =RHS. \end{align*}\] Finally, the left hand side of equation \(\left(3\right)\) is \[\begin{align*} -x+5y-4z & =-2+5\left(-1\right)-4\left(3\right)\\ & =-2-5-12\\ & =-19\\ & =RHS. \end{align*}\]
Example 2
Solve the following simultaneous equations for \(x,y\) and \(z\) \[\begin{align*} 3x-y+2z & =3\\ 2y-5z & =-1\\ x+y+z & =4. \end{align*}\]
Solution: The augmented matrix is \[\begin{align*} \left[\begin{array}{ccc} 3 & -1 & 2\\ 0 & 2 & -5\\ 1 & 1 & 1 \end{array}\left|\begin{array}{c} 3\\ -1\\ 4 \end{array}\right.\right]. \end{align*}\] We first interchange rows \(1\)and \(3.\) This puts a one in the top left corner of the matrix and makes the arithmetic easier: \[\begin{align*} \begin{array}{c} R_{1}'=R_{3}\\ \\ R_{3}'=R_{1} \end{array}\left[\begin{array}{ccc} 1 & 1 & 1\\ 0 & 2 & -5\\ 3 & -1 & 2 \end{array}\left|\begin{array}{c} 4\\ -1\\ 3 \end{array}\right.\right]. \end{align*}\] We now want a zero in the first position of row \(3\). We subtract \(3R_{1}\) from \(R_{3}\)to get: \[\begin{align*} \begin{array}{c} \\ \\ R_{3}'=R_{3}-3R_{1} \end{array}\left[\begin{array}{ccc} 1 & 1 & 1\\ 0 & 2 & -5\\ 0 & -4 & -1 \end{array}\left|\begin{array}{c} 4\\ -1\\ -9 \end{array}\right.\right]. \end{align*}\] Now we want a zero in row \(3\)column \(2\). We get this by adding \(2R_{2}\) to \(R_{3}\): \[\begin{align*} \begin{array}{c} \\ \\ R_{3}'=R_{3}+2R_{2} \end{array}\left[\begin{array}{ccc} 1 & 1 & 1\\ 0 & 2 & -5\\ 0 & 0 & -11 \end{array}\left|\begin{array}{c} 4\\ -1\\ -11 \end{array}\right.\right]. \end{align*}\] From row \(3\), \(-11z=-11\) so \(z=1.\) From row \(2\) and substituting \(z=1\) we get \[\begin{align*} 2y-5z & =-1\\ 2y-5\left(1\right) & =-1\\ 2y & =4\\ y & =2. \end{align*}\] From row \(3\) and substituting for \(x\)and \(y\) we have \[\begin{align*} 3x-y+2z & =3\\ 3x-2+2\left(1\right) & =3\\ 3x & =3\\ x & =1. \end{align*}\] So the solution is \(x=1,\,y=2\) and \(z=1.\)
Example 3
Solve the equations: \[\begin{align*} 2x-2y+2z & =-6\\ 3x+4y+z & =-2\\ 2x+6y+3z & =2. \end{align*}\]
Solution: The augmented matrix is \[\begin{align*} \left[\begin{array}{ccc} 2 & -2 & 2\\ 3 & 4 & 1\\ 2 & 6 & 3 \end{array}\left|\begin{array}{c} -6\\ -2\\ 2 \end{array}\right.\right]. \end{align*}\]
The first step is to try and get a 1 in the top left hand corner of the matrix. In example 2 we did that by interchanging rows. In this case, that won’t work. However row \(1\) can be divided by \(2\) to get \[\begin{align*} \begin{array}{c} R_{1}'=R_{1}/2\\ \\ \\ \end{array}\left[\begin{array}{ccc} 1 & -1 & 1\\ 3 & 4 & 1\\ 2 & 6 & 3 \end{array}\left|\begin{array}{c} -3\\ -2\\ 2 \end{array}\right.\right]. \end{align*}\] Now we proceed in the usual way. In this example we do not put in all the comments. \[\begin{align*} \begin{array}{c} \\ R_{2}'=R_{2}-3R_{1}\\ \\ \end{array}\left[\begin{array}{ccc} 1 & -1 & 1\\ 0 & 7 & -2\\ 2 & 6 & 3 \end{array}\left|\begin{array}{c} -3\\ 7\\ 2 \end{array}\right.\right] \end{align*}\] \[\begin{align*} \begin{array}{c} \\ \\ R_{3}'=R_{3}-2R_{1} \end{array}\left[\begin{array}{ccc} 1 & -1 & 1\\ 0 & 7 & -2\\ 0 & 8 & 1 \end{array}\left|\begin{array}{c} -3\\ 7\\ 8 \end{array}\right.\right] \end{align*}\] \[\begin{align*} \begin{array}{c} \\ \\ R_{3}'=7R_{3}-8R_{2} \end{array}\left[\begin{array}{ccc} 1 & -1 & 1\\ 0 & 7 & -2\\ 0 & 0 & 23 \end{array}\left|\begin{array}{c} -3\\ 7\\ 0 \end{array}\right.\right]. \end{align*}\]
From \(R_{3}\)we have \(23z=0\) and so \(z=0.\) Substituting this into \(R_{2}\) gives \[\begin{align*} 7y-2z & =7\\ 7y-2\left(0\right) & =7\\ 7y & =7\\ y & =1. \end{align*}\] Substituting \(z=0,\,y=1\) into \(R_{1}\) we get \[\begin{align*} x-y+z & =-3\\ x-1+0 & =-3\\ x & =-2. \end{align*}\] The solution is \(x=-2,\,y=1,\,z=0\).
Infinite Number of Solutions
In all the examples above we had a unique solution. That is, \(x,\,y\) and \(z\) were associated with a single number. It is possible that a set of simultaneous equations has an infinite number of solutions. Imagine after using row operations you get an augmented matrix like \[\begin{align*} \left[\begin{array}{ccc} a & b & c\\ 0 & e & f\\ 0 & 0 & 0 \end{array}\left|\begin{array}{c} d\\ g\\ 0 \end{array}\right.\right]. \end{align*}\] In this case \(R_{3}\) tells us nothing. We basically have \(2\) equations and \(3\) unknowns. In this case we will have an infinite number of solutions and the variables \(x,y\) and \(z\) will be in terms of some parameter. The following example illustrates this case.
Example 4
Solve the following set of equations: \[\begin{align*} x+y+z & =3\\ 2x-y+z & =5\\ 3x+2z & =8. \end{align*}\]
Solution: The augmented matrix is \[\begin{align*} \left[\begin{array}{ccc} 1 & 1 & 1\\ 2 & -1 & 1\\ 3 & 0 & 2 \end{array}\left|\begin{array}{c} 3\\ 5\\ 8 \end{array}\right.\right]. \end{align*}\] Performing row operations we get \[\begin{align*} \begin{array}{c} \\ R_{2}'=R_{2}-2R_{1}\\ \\ \end{array}\left[\begin{array}{ccc} 1 & 1 & 1\\ 0 & -3 & -1\\ 3 & 0 & 2 \end{array}\left|\begin{array}{c} 3\\ -1\\ 8 \end{array}\right.\right] \end{align*}\] \[\begin{align*} \begin{array}{c} \\ \\ R_{3}'=R_{3}-3R_{1} \end{array}\left[\begin{array}{ccc} 1 & 1 & 1\\ 0 & -3 & -1\\ 0 & -3 & -1 \end{array}\left|\begin{array}{c} 3\\ -1\\ -1 \end{array}\right.\right] \end{align*}\] \[\begin{align*} \begin{array}{c} \\ \\ R_{3}'=R_{3}-R_{2} \end{array}\left[\begin{array}{ccc} 1 & 1 & 1\\ 0 & -3 & -1\\ 0 & 0 & 0 \end{array}\left|\begin{array}{c} 3\\ -1\\ 0 \end{array}\right.\right]. \end{align*}\] We can go no further with elementary row operations and so start back substitution. Row \(3\) tells us nothing. From row \(2\) we have \[\begin{align*} -3y-z & =-1\\ 3y+z & =1. \end{align*}\] This is an equation with two unknowns. In this case we let one of the variables, either \(y\) or \(z\) be free. That is we let \(y\) or \(z\) be equal to some parameter \(t\in\mathbb{R}\). It doesn’t matter which variable you choose to be free, though the answer will look different. We will set \(z=t\) then we have \[\begin{align*} 3y+z & =1\\ 3y+t & =1\\ 3y & =1-t\\ y & =\frac{1-t}{3}. \end{align*}\] From row \(1\) and substituting \(z=t\) and \(y=\left(1-t\right)/3\) we have \[\begin{align*} x+y+z & =3\\ x+\frac{1-t}{3}+t & =3\\ 3x+1-t+3t & =9\\ 3x & =8-2t\\ x & =\frac{8-2t}{3}. \end{align*}\] So the solution here is \[\begin{align*} x & =\frac{8-2t}{3},y=\frac{1-t}{3},z=t,\;t\in\mathbb{R}. \end{align*}\] This gives us an infinite number of solutions because \(t\) can be any real number. To check the solution you can pick any value of \(t,\)determine \(x,y\) and \(z\) and substitute in the original equations. For example let \(t=0\).3 Here we took \(t=0\) because it is easy to get the corresponding \(x,\,y\) and \(z\) values. But you can pick any value of \(t\). Once you choose \(t\), there will be a corresponding value of \(x,\,y\) and \(z.\) These \(x,\,y\) and \(z\) values will satisfy the original equations. Note that picking a value of \(t\) and checking if the corresponding \(x,\,y\) and \(z\) values will the original equation is not a proof that your solution is correct. A real proof would have to consider all values of \(t.\) However it is a useful check. Then\[\begin{align*} x & =\frac{8}{3},y=\frac{1}{3},z=0. \end{align*}\] Substituting in equation 1 gives \[\begin{align*} LHS & =x+y+z\\ & =\frac{8}{3}+\frac{1}{3}+0\\ & =\frac{9}{3}\\ & =3\\ & =RHS. \end{align*}\] You can substitute into the second and third equation to check this solution is correct.
Exercises
Find the solutions to the following systems of equations:
\[\begin{array}{llcll} 1. & x-y-2z=-6 & \qquad\qquad\qquad\qquad & 2. & 2x+y+2z=4\\ & 2x-3y+3z=1 & & & 2x+4y-2z=6\\ & 3x-y+4z=4 & & & -y+3z=1 \end{array}\]
\[\begin{array}{lllccll} 3. & x_{1}-x_{2}-2x_{3}=1 & & & \quad & 4. & x-2y+z-w=0\\ & -3x_{1}+2x_{2}+4x_{3}=-3 & \quad & \quad & & & 2x+4y-3z=0\\ & 2x_{1}+x_{2}+x_{3}=1 & \quad & \quad & & & 3x+2y+2z-w=0 \end{array}\]
\(x=-1,\,y=1,\,z=2\)
\(x=0,\,y=2,\,z=1\)
\(x_{1}=1,\,x_{2}=-2,\,x_{3}=1\)
\(x=\frac{1}{2}t,\,y=-\frac{1}{4}t,\,z=0,\,w=t\)
Download this page, M6 Systems of equations (PDF 181KB)
What's next... M7 Types of Solutions
