M7 Types of solutions
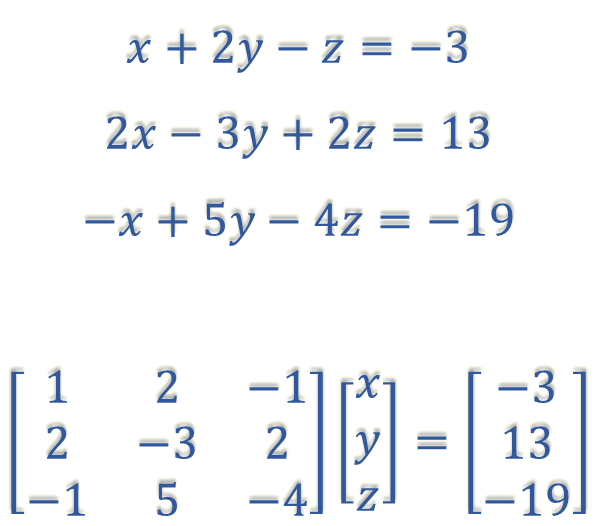
For any system of equations, there may be:
Infinitely many solutions
No solution
A unique solution
This module discusses these possibilities.
Coefficient Matrix
Consider the following system of equations: \[\begin{align*} 2x+4y-z & =9\\ x-y+2z & =-4\\ -x+y-z & =3 \end{align*}\] These may be written in the matrix form: \[\begin{align*} \left[\begin{array}{ccc} 2 & 4 & -1\\ 1 & -1 & 2\\ -1 & 1 & -1 \end{array}\right]\left[\begin{array}{c} x\\ y\\ z \end{array}\right] & =\left[\begin{array}{c} 9\\ -4\\ 3 \end{array}\right]. \end{align*}\] The matrix \[\begin{align*} \left[\begin{array}{ccc} 2 & 4 & -1\\ 1 & -1 & 2\\ -1 & 1 & -1 \end{array}\right] \end{align*}\] is called the coefficient matrix because it contains the coefficients of the variables \(x,y\) and \(z\) in the system of equations.
What Does the Coefficient Matrix Tell Us?
The coefficient matrix can be used to find information about the number of solutions to a system of equations. For any system of equations, if the coefficient matrix is:
Singular (that is the determinant \(=0\)) there will be an infinite number of solutions or no solutions.
Non-singular (determinant \(\neq0\)) there will be a unique solution.
Infinitely Many Solutions
Example 1
Consider the system of equations \[\begin{align*} x+2y-z & =3\\ x+3y & =4\\ -x-y+2z & =-2 \end{align*}\]
The augmented matrix for this system is \[\begin{align*} \left[\begin{array}{ccc} 1 & 2 & -1\\ 1 & 3 & 0\\ -1 & -1 & 2 \end{array}\left|\begin{array}{c} 3\\ 4\\ -2 \end{array}\right.\right]. \end{align*}\] Using elementary row operations we get: \[\begin{align*} \begin{array}{c} \\ R_{2}'=R_{2}-R_{1}\\ R_{3}'=R_{3}+R_{1} \end{array}\left[\begin{array}{ccc} 1 & 2 & -1\\ 0 & 1 & 1\\ 0 & 1 & 1 \end{array}\left|\begin{array}{c} 3\\ 1\\ 1 \end{array}\right.\right] \end{align*}\] \[\begin{align*} \begin{array}{c} \\ \\ R_{3}'=R_{3}-R_{2} \end{array}\left[\begin{array}{ccc} 1 & 2 & -1\\ 0 & 1 & 1\\ 0 & 0 & 0 \end{array}\left|\begin{array}{c} 3\\ 1\\ 0 \end{array}\right.\right] \end{align*}\] Row \(3\) tells us that \(0x+0y+0z=0.\) This is true for any value of \(x,y\) or \(z.\) So we are able to set any one of these variables to some number \(t\in\mathbb{R}\).1 It can only be one variable as there other equations to be satisfied in \(R_{2}\) and \(R_{1}.\) For this example,2 Even though we set \(z=t,\) we could set either \(x=t\) or \(y=t\). We still get a solution to the system of equations but it will look different. we set \(z=t.\) From \(R_{2}\) and substituting \(t\) for \(z\) we have \[\begin{align*} y+z & =1\\ y+t & =1\\ y & =1-t. \end{align*}\] Now from \(R_{1}\), substituting \(z=t,\,y=1-t\) we have \[\begin{align*} x+2y-z & =3\\ x+2\left(1-t\right)-t & =3\\ x+2-2t-t & =3\\ x & =1+3t. \end{align*}\] So the solution is \(x=1+3t,\,y=1-t\) and \(z=t\) where \(t\in\mathbb{R}\).3 As there are an infinite number of choices for \(t,\) there are an infinite number of solutions to the system of equations.
In general if the reduced augmented matrix has one or more rows of zeros, there will be an infinite number of solutions to the system of equations.4 You may recall that the determinant of a matrix with a row of zeros is zero. Hence the matrix is singular.
Example 2
Consider the system of equations \[\begin{align*} x+2y-z & =3\\ 2x+4y-2z & =6\\ -5x-10y+5z & =-15 \end{align*}\]
The augmented matrix for this system is \[\begin{align*} \left[\begin{array}{ccc} 1 & 2 & -1\\ 2 & 4 & -2\\ -5 & -10 & 5 \end{array}\left|\begin{array}{c} 3\\ 6\\ -15 \end{array}\right.\right]. \end{align*}\] Using elementary row operations we get \[\begin{align*} \begin{array}{c} \\ R_{2}'=R_{2}-2R_{1}\\ R_{3}'=R_{3}+5R_{1} \end{array}\left[\begin{array}{ccc} 1 & 2 & -1\\ 0 & 0 & 0\\ 0 & 0 & 0 \end{array}\left|\begin{array}{c} 3\\ 0\\ 0 \end{array}\right.\right]. \end{align*}\] We have only one equation and three unknowns. In this case we must let two of the three variables be free. For example, we set \(z=t\), where \(t\in\mathbb{R}\) and \(y=s,\) where \(s\in\mathbb{R}\) .5 It doesn’t matter which two variables are selected to be a parameter \(s\) or \(t.\) We could set \(x=s\) and \(y=t.\) Substituting in row \(1\) gives: \[\begin{align*} s+2t-z & =3\\ z & =s+2t-3. \end{align*}\] While this looks different to the solution at left, it is still a valid solution to the set of equations. Substituting into \(R_{1}\) we get \[\begin{align*} x+2y-z & =3\\ x+2s-t & =3\\ x & =3-2s+t. \end{align*}\] So the solution is \(x=3-2s+t,\,y=s,\,z=t\) where \(s\in\mathbb{R}\) and \(t\in\mathbb{R}\).
No Solutions
Consider the system of equations \[\begin{align*} x+2y-2z & =3\\ 2x+y+z & =4\\ 3y-5z & =-1. \end{align*}\] The augmented matrix for this system is \[\begin{align*} \left[\begin{array}{ccc} 1 & 2 & -2\\ 2 & 1 & 1\\ 0 & 3 & -5 \end{array}\left|\begin{array}{c} 3\\ 4\\ -1 \end{array}\right.\right]. \end{align*}\] Using elementary row operations we get: \[\begin{align*} \begin{array}{c} \\ R_{2}'\\ \\ \end{array}=R_{2}-2R_{1}\left[\begin{array}{ccc} 1 & 2 & -2\\ 0 & -3 & 5\\ 0 & 3 & -5 \end{array}\left|\begin{array}{c} 3\\ -2\\ -1 \end{array}\right.\right] \end{align*}\] \[\begin{align*} \begin{array}{c} \\ \\ R_{3}'=R_{3}+R_{2} \end{array}\left[\begin{array}{ccc} 1 & 2 & -2\\ 0 & -3 & 5\\ 0 & 0 & 0 \end{array}\left|\begin{array}{c} 3\\ -1\\ -3 \end{array}\right.\right]. \end{align*}\] In this case, \(R_{3}\) says that \(0x+0y+0z=-3.\) This is not possible because regardless of the choice of \(x,y\) and \(z\) the LHS must be zero. In this case there are no solutions and we call the system of equations inconsistent.
Unique Solutions
Consider the system of equations \[\begin{align*} 2x+4y-z & =9\\ x-y+2z & =-4\\ -x+y-z & =3 \end{align*}\]
The augmented matrix for this system is \[\begin{align*} \left[\begin{array}{ccc} 2 & 4 & -1\\ 1 & -1 & 2\\ -1 & 1 & -1 \end{array}\left|\begin{array}{c} 9\\ -4\\ 3 \end{array}\right.\right]. \end{align*}\] Using elementary row operations we get \[\begin{align*} \begin{array}{c} R_{1}'=R_{2}\\ R_{2}'=R_{1}\\ \\ \end{array}\left[\begin{array}{ccc} 1 & -1 & 2\\ 2 & 4 & -1\\ -1 & 1 & -1 \end{array}\left|\begin{array}{c} -4\\ 9\\ 3 \end{array}\right.\right] \end{align*}\] \[\begin{align*} \begin{array}{c} \\ R_{2}'=R_{2}-2R_{1}\\ R_{3}'=R_{3}+R_{1} \end{array}\left[\begin{array}{ccc} 1 & -1 & 2\\ 0 & 6 & -5\\ 0 & 0 & 1 \end{array}\left|\begin{array}{c} -4\\ 17\\ -1 \end{array}\right.\right]. \end{align*}\] From row \(3\) we have \(z=-1.\) Substituting this into row 2 we have \[\begin{align*} 6y-5z & =17\\ 6y+5 & =17\\ 6y & =12\\ y & =2. \end{align*}\] Substituting for \(z\) and \(y\) in row 1 gives: \[\begin{align*} 2x+4y-z & =9\\ 2x+4\left(2\right)-\left(-1\right) & =9\\ 2x+8+1 & =9\\ 2x & =0\\ x & =0. \end{align*}\] So the solution is \(x=0,\,y=2,\,z=-1\).
Exercises
Find the solutions (if they exist) to the following systems of equations:
\[\begin{array}{lllll} 1. & x+2y-z=5 & \quad\quad & 2. & x+2y-2z=7\\ & 3x-y+2z=1 & & & 2x-y-z=-3\\ & 2x-y+3z=0 & & & -x-2y+2z=1 \end{array}\]
\[\begin{array}{lllll} 3. & 2x-y+3z=-3 & & 4. & x+2y-z=3\\ & x+2y+z=-4 & & & -x+y-2z=-3\\ & 4x+3y+5z=-11 & & & 3x+3z=9 \end{array}\]
\(x=1,\,y=2,\,z=0\)
No solution
\(x=-\frac{7t}{5}-2,\,y=\frac{t}{5}-1,\,z=t\;\) (Your answer may be different if you choose \(y=t\) or \(x=t.)\)
\(x=3-t,\,y=t,\,z=t\;\) (Your answer may be different if you choose \(y=t\) or \(x=t.)\)
Download this page, M7 Types of Solutions (PDF 173KB)
What's next... M8 Inverse of a 2x2 matrix
