M1 Matrices: Introduction
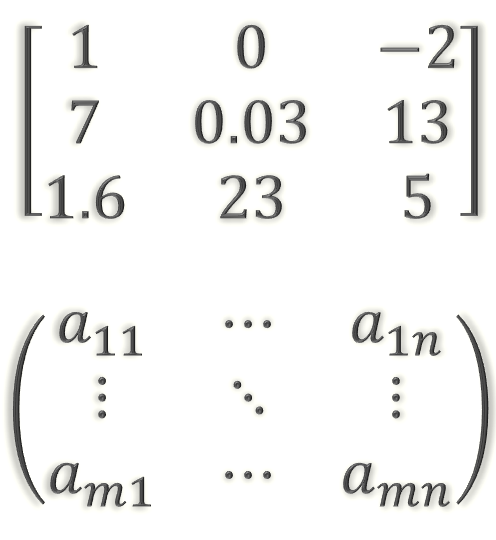
A matrix is a rectangular array of elements.
Matrices are usually denoted by upper case letters.
The elements are usually written within brackets.
The order or shape of the matrix is determined by the number of rows and columns of the matrix.
The number of rows is always given first then the number of columns. Example. \[\begin{align*} A & =\left[\begin{array}{ccc} 1 & 2 & -9\\ 2 & 5 & -3 \end{array}\right] \end{align*}\]
\(A\) has 2 rows and 3 columns and is called a \(2\times3\) matrix.1 This is verbally stated as a 2 by 3 matrix.
A matrix with \(m\) rows and \(n\) columns is called a matrix of order \(m\times n\).2 This is verbally termed an “m by n matrix”.
Square Matrix
A matrix with the same number of rows and columns is called a square matrix.
Example: \[\begin{align*} B & =\left[\begin{array}{cc} 2 & 3\\ 2 & 5 \end{array}\right] \end{align*}\]
\(B\) is a square \(2\times2\) matrix
Unit Matrix
A unit (or identity) matrix is a square matrix with diagonal elements equal to one, and all other elements equal to zero. The unit matrix is usually denoted by \(I\).
\(I_{3}\) is a \(3\times3\) unit matrix
Example: \[\begin{align*} I_{3} & =\left[\begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 & 1 \end{array}\right] \end{align*}\]
Row Matrix
A matrix with one row is called a row matrix.
Example: \[\begin{align*} D & =\left[\begin{array}{cccc} 2 & 1 & 0 & 4\end{array}\right] \end{align*}\] is a \(1\times4\) row matrix
Column Matrix
A matrix with one column is called a column matrix.
Example: \[\begin{align*} E & =\left[\begin{array}{c} 2\\ -4\\ 1 \end{array}\right] \end{align*}\]
is a \(3\times1\) column matrix
Zero Matrix
A zero matrix has all elements equal to zero. A zero matrix can be written as \(0\).
Example: \[\begin{align*} 0 & =\left[\begin{array}{cc} 0 & 0\\ 0 & 0 \end{array}\right] \end{align*}\]
is a \(2\times2\) zero matrix
Equal Matrices
For two matrices to be equal, they must be the same shape and the corresponding elements must be equal.
If \(A\) equals \(B\) then \[\begin{align*} A & =\left[\begin{array}{ccc} 2 & 5 & b\\ 5 & 3 & 1\\ 2 & 0 & -2 \end{array}\right] & B & =\left[\begin{array}{ccc} 2 & 5 & 7\\ 5 & a & 1\\ 2 & 0 & -2 \end{array}\right] \end{align*}\]
If \(A\) and \(B\) are equal then \(a\) = 3 and \(b\) = 7.
Exercise:
- Write down the order of the following matrices.
\(\left[\begin{array}{ccc} 7 & -5 & 0\\ 6 & 2 & -1 \end{array}\right]\)
\(\left[\begin{array}{cc} 0 & 2\\ 1 & 1 \end{array}\right]\)
\(\left[\begin{array}{c} 2\\ -4\\ 1\\ 1 \end{array}\right]\)
\(\left[\begin{array}{cc} 1 & 1\\ 3 & 0\\ -2 & 3 \end{array}\right]\)
- Which of the following matrices are equal?
\[\begin{align*} A & =\left[\begin{array}{cc} 3 & 0\\ 1 & -2 \end{array}\right] & B & =\left[\begin{array}{cc} 3 & 1\end{array}\right] & C & =\left[\begin{array}{cc} 3 & 0\end{array}\right] & D & =\left[\begin{array}{cc} 3 & 0\\ 1 & -2 \end{array}\right] \end{align*}\]
\[\begin{align*} E & =\left[\begin{array}{ccc} 3 & 5 & 1\\ 2 & 0 & 1 \end{array}\right] & F & =\left[\begin{array}{cc} 0 & 3\end{array}\right] & G & =\left[\begin{array}{ccc} 3 & 5 & 1\\ 2 & 0 & 1\\ 1 & 3 & 0 \end{array}\right] \end{align*}\]
\[\begin{array}{lllllllccc} 1.\;a)\,2\times3 & & b)\,2\times2 & & c)\,4\times1 & & d)\,3\times2 & & & 2.\,A\textrm{ and $D$ }\end{array}\]
Download this page, M1 Matrices: Introduction (PDF 172KB)
What's next... M2 Addition and subtraction of matrices
