M4 Determinant of a matrix
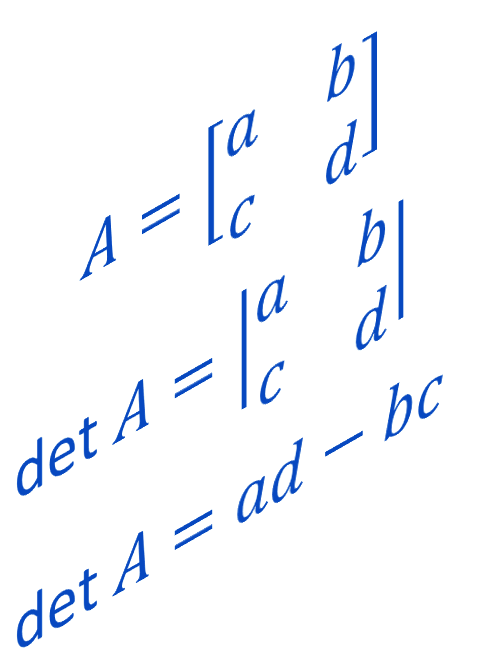
A determinant is a number that can be calculated for any square matrix. The determinant is used in calculating vector cross products, eigenvalues, eigenvectors and solving simultaneous equations.
Determinant of a \(2\times2\) Matrix
The determinant of a \(2\times2\) matrix is called a second order determinant.
Let \[\begin{align*} A & =\left[\begin{array}{cc} a & b\\ c & d \end{array}\right]. \end{align*}\] The determinant of \(A\) is denoted by \(\det A\) or \(\left|A\right|\) and is defined to be \[\begin{align*} \left|A\right| & =\left|\begin{array}{cc} a & b\\ c & d \end{array}\right|\\ & =ad-bc. \end{align*}\]
Examples
\(\left|\begin{array}{cc} 2 & 3\\ 1 & 5 \end{array}\right|=2\times5-1\times3=10-3=7.\)
\(\left|\begin{array}{cc} 3 & 2\\ -1 & 1 \end{array}\right|=3\times1-\left(-1\right)\times2=3-\left(-2\right)=3+2=5.\)
\(\left|\begin{array}{cc} -2 & -1\\ 6 & 3 \end{array}\right|=\left(-2\right)\times3-6\times\left(-1\right)=-6+6=0.\)
Singular Matrices
A matrix that has a determinant of zero is called a singular matrix.1 Singular matrices do not have an inverse. If the determinant is not zero, the matrix is called non-singular.
See Exercise 1 for some practice.
Determinant of a \(3\times3\) Matrix
The determinant of a \(3\times3\) matrix is called a third order determinant.
Let \[\begin{align*} B & =\left[\begin{array}{ccc} a_{1} & b_{1} & c_{1}\\ a_{2} & b_{2} & c_{2}\\ a_{3} & b_{3} & c_{3} \end{array}\right] \end{align*}\] then the determinant of \(B\) is calculated by expanding about any row or column and evaluating the resulting second order determinant.2 It is amazing that the value of the determinant is the same regardless of which row or column we expand along.
Expanding along row one. Multiply \(a_{1}\) by the second order determinant obtained by ignoring the row and column occupied by \(a_{1}.\) We get \[ a_{1}\left|\begin{array}{cc} b_{2} & c_{2}\\ b_{3} & c_{3} \end{array}\right|. \]
Now multiply \(b_{1}\) by the second order determinant obtained by ignoring the row and column occupied by \(b_{1}.\) We get \[ b_{1}\left|\begin{array}{cc} a_{2} & c_{2}\\ a_{3} & c_{3} \end{array}\right|. \]
Now multiply \(c_{1}\) by the second order determinant obtained by ignoring the row and column occupied by \(c_{1}.\) We get \[ c_{1}\left|\begin{array}{cc} a_{2} & b_{2}\\ a_{3} & b_{3} \end{array}\right|. \]
The determinant of \(B\) is then \[\begin{align*} \left|B\right| & =\left|\begin{array}{ccc} a_{1} & b_{1} & c_{1}\\ a_{2} & b_{2} & c_{2}\\ a_{3} & b_{3} & c_{3} \end{array}\right|\\ & =a_{1}\left|\begin{array}{cc} b_{2} & c_{2}\\ b_{3} & c_{3} \end{array}\right|-b_{1}\left|\begin{array}{cc} a_{2} & c_{2}\\ a_{3} & c_{3} \end{array}\right|+c_{1}\left|\begin{array}{cc} a_{2} & b_{2}\\ a_{3} & b_{3} \end{array}\right|. \end{align*}\] Note the change in sign on the second term. In fact when calculating determinants, it is good to have the following picture in mind: \[ \left|\begin{array}{ccc} + & - & +\\ - & + & -\\ + & - & + \end{array}\right| \] these signs should then be applied to the respective elements.
In the case above we expanded along row one. We get the same value of determinant regardless of which row or column we expand about. Now we expand along column \(2\) to get: \[\begin{align*} \left|B\right| & =\left|\begin{array}{ccc} a_{1} & b_{1} & c_{1}\\ a_{2} & b_{2} & c_{2}\\ a_{3} & b_{3} & c_{3} \end{array}\right|\\ & =-b_{1}\left|\begin{array}{cc} a_{2} & c_{2}\\ a_{3} & c_{3} \end{array}\right|+b_{2}\left|\begin{array}{cc} a_{1} & c_{1}\\ a_{3} & c_{3} \end{array}\right|-b_{3}\left|\begin{array}{cc} a_{1} & c_{1}\\ a_{2} & c_{2} \end{array}\right|. \end{align*}\] Again, note the sign changes.
Example 1
Calculate the determinant of \[ A=\left[\begin{array}{ccc} 2 & 1 & 3\\ 1 & -1 & 2\\ 2 & 1 & 4 \end{array}\right]. \]
Solution 1:
Expanding along row one we get: \[\begin{align*} \left|A\right| & =\left|\begin{array}{ccc} 2 & 1 & 3\\ 1 & -1 & 2\\ 2 & 1 & 4 \end{array}\right|\\ & =2\left|\begin{array}{cc} -1 & 2\\ 1 & 4 \end{array}\right|-1\left|\begin{array}{cc} 1 & 2\\ 2 & 4 \end{array}\right|+3\left|\begin{array}{cc} 1 & -1\\ 2 & 1 \end{array}\right|\\ & =2\left(\left(-1\right)\times4-1\times2\right)-\left(1\times4-2\times2\right)+3\left(1\times1-2\times\left(-1\right)\right)\\ & =2\left(-4-2\right)-\left(4-4\right)+3\left(1+2\right)\\ & =-12+9\\ & =-3. \end{align*}\]
Solution 2:
This time we will expand about column 2 to get: \[\begin{align*} \left|A\right| & =\left|\begin{array}{ccc} 2 & 1 & 3\\ 1 & -1 & 2\\ 2 & 1 & 4 \end{array}\right|\\ & =-1\left|\begin{array}{cc} 1 & 2\\ 2 & 4 \end{array}\right|-1\left|\begin{array}{cc} 2 & 3\\ 2 & 4 \end{array}\right|-1\left|\begin{array}{cc} 2 & 3\\ 1 & 2 \end{array}\right|\\ & =-1\left(1\times4-2\times2\right)-\left(2\times4-2\times3\right)-1\left(2\times2-1\times3\right)\\ & =-1\left(4-4\right)-\left(8-6\right)-1\left(4-3\right)\\ & =-2-1\\ & =-3. \end{align*}\] as before.
Example 2
Calculate the determinant of \[ B=\left[\begin{array}{ccc} 1 & 3 & -2\\ 1 & -1 & 3\\ 2 & 6 & -4 \end{array}\right]. \]
Solution:
Expanding along column 1 we get: \[\begin{align*} \left|B\right| & =\left|\begin{array}{ccc} 1 & 3 & -2\\ 1 & -1 & 3\\ 2 & 6 & -4 \end{array}\right|\\ & =1\left|\begin{array}{cc} -1 & 3\\ 6 & -4 \end{array}\right|-1\left|\begin{array}{cc} 3 & -2\\ 6 & -4 \end{array}\right|+2\left|\begin{array}{cc} 3 & -2\\ -1 & 3 \end{array}\right|\\ & =1\left(\left(-1\right)\times\left(-4\right)-6\times3\right)-1\left(3\times\left(-4\right)-6\times\left(-2\right)\right)+2\left(3\times3-\left(-1\right)\times\left(-2\right)\right)\\ & =\left(4-18\right)-\left(-12-\left(-12\right)\right)+2\left(9-2\right)\\ & =-14+14\\ & =0. \end{align*}\] Note that row \(3\) of \(B\) is a multiple of row \(1.\) In general, when a row is a multiple of another row, the determinant is zero. Also if a column is a multiple of another column, the determinant is zero.
Example 3
Calculate the determinant of \[ C=\left[\begin{array}{ccc} 1 & 5 & 6\\ 3 & -2 & 2\\ 4 & 0 & 1 \end{array}\right]. \] Solution:
This time it is best to expand about column \(2\) or row \(3.\) This is because column \(2\) or row \(3\) contains a zero which makes the calculation easier. Expanding along row \(3\) we get: \[\begin{align*} \left|C\right| & =\left|\begin{array}{ccc} 1 & 5 & 6\\ 3 & -2 & 2\\ 4 & 0 & 1 \end{array}\right|\\ & =4\left|\begin{array}{cc} 5 & 6\\ -2 & 2 \end{array}\right|-0\left|\begin{array}{cc} 1 & 6\\ 3 & 2 \end{array}\right|+1\left|\begin{array}{cc} 1 & 5\\ 3 & -2 \end{array}\right|\\ & =4\left(5\times2-\left(-2\right)\times6\right)+1\left(1\times\left(-2\right)-3\times5\right)\\ & =4\left(10+12\right)+1\left(-2-15\right)\\ & =88-17\\ & =71. \end{align*}\]
See Exercise 2 for some practice.
Evaluating Higher Order Determinants
Fourth order determinants can be evaluated using third order determinants and fifth order by using fourth order and so forth. When doing this, you need to apply the following signs \[ \left|\begin{array}{ccccc} + & - & + & - & \cdots\\ - & + & - & + & \cdots\\ + & - & + & - & \cdots\\ - & + & - & + & \cdots\\ \vdots & \vdots & \vdots & \vdots & \ddots \end{array}\right| \]
Calculators capable of doing matrix algebra can also be used to evaluate determinants.
Exercise 1
Evaluate the following determinants:
\[\begin{align*} \begin{array}{lllll} a)\,\left|\begin{array}{cc} 2 & 5\\ 1 & 2 \end{array}\right| & b)\,\left|\begin{array}{cc} -1 & 1\\ -2 & 5 \end{array}\right| & c)\,\left|\begin{array}{cc} 2 & -3\\ -2 & 6 \end{array}\right| & d)\,\left|\begin{array}{cc} 0 & -3\\ 1 & 0 \end{array}\right| & e)\,\left|\begin{array}{cc} 1 & -3\\ -3 & 9 \end{array}\right|.\end{array} \end{align*}\]
\[\begin{align*} \begin{array}{lllll} a)\,-1 & b)\,-3 & c)\,18 & d)\,3 & e)\,0\end{array} \end{align*}\]
Exercise 2
Evaluate the following determinants:
\[\begin{align*} \begin{array}{lllll} a)\,\left|\begin{array}{ccc} -1 & 1 & 3\\ 2 & 3 & 1\\ -1 & 1 & 5 \end{array}\right| & b)\,\left|\begin{array}{ccc} 3 & -1 & -3\\ 1 & 4 & 1\\ 3 & 1 & 1 \end{array}\right| & c)\,\left|\begin{array}{ccc} -1 & 5 & 2\\ 3 & -5 & -6\\ -2 & 3 & 4 \end{array}\right| & d)\,\left|\begin{array}{ccc} -2 & 3 & -3\\ 6 & 0 & 2\\ 2 & 0 & 4 \end{array}\right| & e)\,\left|\begin{array}{ccc} a & 0 & 0\\ 0 & b & 0\\ 0 & 0 & c \end{array}\right|.\end{array} \end{align*}\]
\[\begin{align*} \begin{array}{lllll} a)\,-10 & b)\,40 & c)\,0 & d)\,-60 & e)\,abc\end{array} \end{align*}\]
Download this page, M4 Determinant of a matrix (PDF 142KB)
What's next... M5 Special Matrices
