V4 Vector product
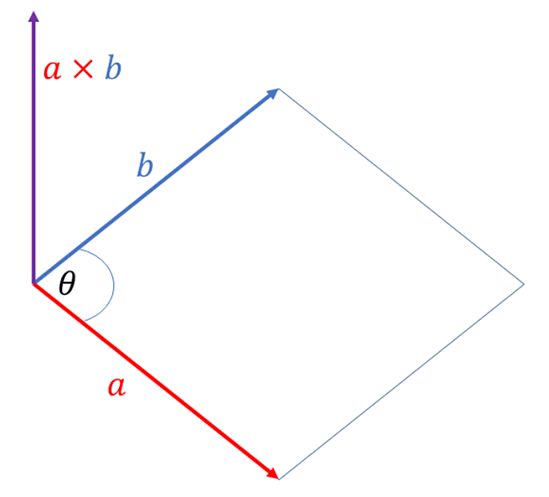
What is a vector product? What is a cross product? The vector product is a vector that is the result of multiplying the magnitudes (size) of two vectors. The magnitude is found using matrices and determinants).
The result of the cross product is another vector, and the direction is perpendicular (normal, at 90 degrees) to the plane of both the original vectors.
There are two ways to multiply two vectors:
The scalar product which gives a number (also called the dot product);
The vector product which gives a vector (also called the cross product).
In this module we consider the vector or cross product.
Definition
Let \(\hat{i},\,\) \(\hat{j}\) and \(\hat{k}\) be unit vectors in the \(x,\,y\) and \(z\) directions respectively. We can write \[\begin{align*} \hat{i} & =\hat{i}+0\hat{j}+0\hat{k}\\ & =\left(1,0,0\right)\\ \hat{j} & =0\hat{i}+\hat{j}+0\hat{k}\\ & =\left(0,1,0\right)\\ \hat{k} & =0\hat{i}+0\hat{j}+\hat{k}\\ & =\left(0,0,1\right). \end{align*}\]
Let the vectors \[\begin{align*} \vec{a} & =a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k} \end{align*}\] and \[\begin{align*} \vec{b} & =b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}. \end{align*}\] The vector, or cross, product of the two vectors \(\vec{a}\) and \(\vec{b}\) is the vector1 Here, \(\left|\vec{a}\right|\) and \(\left|\vec{b}\right|\) are the magnitudes of the vectors \(\vec{a}\) and \(\vec{b}\). \[\begin{align*} \vec{a}\times\vec{b} & =\left|\vec{a}\right|\left|\vec{b}\right|\sin\left(\theta\right)\,\hat{n} & \left(1\right) \end{align*}\] where \(\hat{n}\) is a unit vector that is perpendicular to both \(\vec{a}\) and \(\vec{b}\) and \(\theta\) is the angle between the vectors \(\vec{a}\) and \(\vec{b}\).
To calculate the cross product, it is more convenient to use the definition2 Here the two vertical delimiters \(\left|\mathbf{A}\right|\) denote the determinant of the matrix \(\mathbf{A}\). For a two by two matrix \[\begin{align*} \mathbf{A} & =\left[\begin{array}{cc} a & b\\ c & d \end{array}\right] \end{align*}\] the determinant \[\begin{align*} \left|\mathbf{A}\right| & =ad-bc. \end{align*}\] This is quite different to the magnitude of a vector \(\left|\vec{a}\right|\). \[\begin{align*} \vec{a}\times\vec{b} & =\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\ a_{1} & a_{2} & a_{3}\\ b_{1} & b_{2} & b_{3} \end{array}\right|\\ & =\hat{i}\left|\begin{array}{cc} a_{2} & a_{3}\\ b_{2} & b_{3} \end{array}\right|-\hat{j}\left|\begin{array}{cc} a_{1} & a_{3}\\ b_{1} & b_{3} \end{array}\right|+\hat{k}\left|\begin{array}{cc} a_{1} & a_{2}\\ b_{1} & b_{2} \end{array}\right|\\ & =\hat{i}\left(a_{2}b_{3}-b_{2}a_{3}\right)-\hat{j}\left(a_{1}b_{3}-b_{1}a_{3}\right)+\hat{k}\left(a_{1}b_{2}-b_{1}a_{2}\right). & \left(2\right) \end{align*}\]
Properties of the Vector or Cross Product
If \(\vec{a}\) is parallel to \(\vec{b}\) then \(\vec{a}\times\vec{b}=\vec{0}\). This follows from eqn \(\left(1\right)\) above3 If \(\vec{a}\) is parallel to \(\vec{b}\) the angle between them is \(0\). Hence from eqn\(\left(1\right)\) \[\begin{align*} \vec{a}\times\vec{b} & =\left|\vec{a}\right|\left|\vec{b}\right|\sin\left(0\right)\,\hat{n}\\ & =\vec{0} \end{align*}\] as \(\sin\left(0\right)=0\).. Note that we should write the answer as the zero vector \(\vec{0}\) instead of the number \(0.\)4 This is a technical point and relates to the concept of a vector space in which certain operations are closed. Closed means if you do operations on a vector you get a vector as a result. In many courses you don’t need to worry about this so writing \(\vec{a}\times\vec{b}=0\) may be allowed. Please see you teacher on this point.
The order in which you take the cross product is important. In fact, \(\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}.\)
The direction of \(\vec{a}\times\vec{b}\) is perpendicular to both \(\vec{a}\) and \(\vec{b}\) in the direction in which your thumb would point if the fingers of your right hand are curled from \(\vec{a}\) to \(\vec{b}\) as shown below
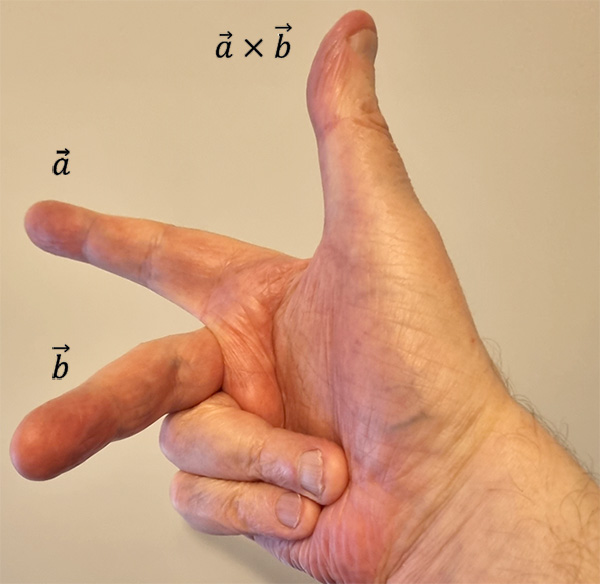
This is called the right hand rule.
Example 1
Find \(\vec{a}\times\vec{b}\) if \(\vec{a}=2\vec{i}+3\vec{j}+\vec{k}\) and \(\vec{b}=5\vec{j}+3\vec{k}\).
Solution: \[\begin{align*} \vec{a}\times\vec{b} & =\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\ 2 & 3 & 1\\ 0 & 5 & 3 \end{array}\right|\\ & =\hat{i}\left(3\times3-5\times1\right)-\hat{j}\left(2\times3-0\times1\right)+\hat{k}\left(2\times5-0\times3\right)\\ & =\left(9-5\right)\hat{i}-\left(6-0\right)\hat{j}+\left(10-0\right)\hat{k}\\ & =4\hat{i}-6\hat{j}+10\hat{k}. \end{align*}\]
Example 2
Find \(\vec{a}\times\vec{b}\) if \(\vec{a}=\left(2,1,1\right)\) and \(\vec{b}=\left(-2,4,0\right)\).
Solution: \[\begin{align*} \vec{a}\times\vec{b} & =\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\ 2 & 1 & 1\\ -2 & 4 & 0 \end{array}\right|\\ & =\hat{i}\left(1\times0-4\times1\right)-\hat{j}\left(2\times0-\left(-2\right)\times1\right)+\hat{k}\left(2\times4-\left(-2\right)\times1\right)\\ & =-4\hat{i}-2\hat{j}+10\hat{k}. \end{align*}\]
Example 3
Find \(\vec{a}\times\vec{b}\) if \(\vec{a}=\left(2,1,1\right)\) and \(\vec{b}=\left(8,4,4\right)\).
Solution: \[\begin{align*} \vec{a}\times\vec{b} & =\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\ 2 & 1 & 1\\ 8 & 4 & 4 \end{array}\right|\\ & =\hat{i}\left(1\times4-4\times1\right)-\hat{j}\left(2\times4-8\times1\right)+\hat{k}\left(2\times4-8\times1\right)\\ & =0\hat{i}-0\hat{j}+0\hat{k}\\ & =0\hat{i}+0\hat{j}+0\hat{k}\\ & =\left(0,0,0\right)\\ & =\vec{0}. \end{align*}\] Note that \(0\hat{i}-0\hat{j}+0\hat{k}=0\hat{i}+0\hat{j}+0\hat{k}\) and that the answer is the vector \(\left(0,0,0\right)=\vec{0},\) not simply the number \(0\) (see footnote 2 above).
Since neither\(\left|\vec{a}\right|\) nor \(\left|\vec{b}\right|\) is zero, from equation \(\left(1\right)\) above, we can see that \(\sin\left(\theta\right)=0\) and so \(\theta=0\) or \(\theta=\pi.\) That is the vectors \(\vec{a}\) and \(\vec{b}\) are in the same or opposite directions. This result could be more quickly obtained by observing that \(\vec{b}=4\vec{a}\) and so \(\vec{a}\) and \(\vec{b}\) are parallel and by property \(\left(1\right)\) of the vector product above, \(\vec{a}\times\vec{b}=\vec{0}\).
Cartesian Unit Vectors
Let \(\hat{i},\,\) \(\hat{j}\) and \(\hat{k}\) be unit vectors in the \(x,\,y\) and \(z\) directions respectively. Then
\[\begin{align*} \hat{i}\times\hat{j} & =\hat{k} & & & \hat{j}\times\hat{k} & =\hat{i} & & & \hat{k}\times\hat{i} & =\hat{j}\\ \hat{i}\times\hat{k} & =-\hat{j} & & & \hat{k}\times\hat{j} & =-\hat{i} & & & \hat{j}\times\hat{i} & =-\hat{k}. \end{align*}\]
These results may be confirmed with the right hand rule or equation \(\left(2\right)\) above.
Example 4
Find \(\hat{i}\times\hat{k}.\)
Solution:
We have \[\begin{align*} \hat{i} & =\hat{i}+0\hat{j}+0\hat{k}\\ \hat{k} & =0\hat{i}+0\hat{j}+\hat{k}. \end{align*}\] Using equation \(\left(2\right),\) \[\begin{align*} \hat{i}\times\hat{k} & =\left|\begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\ 1 & 0 & 0\\ 0 & 0 & 1 \end{array}\right|\\ & =\hat{i}\left(1\times0-0\times0\right)-\hat{j}\left(1\times1-0\times0\right)+\hat{k}\left(1\times0-0\times0\right)\\ & =-\hat{j}. \end{align*}\]
Exercise 1
Calculate the following.
\(\text{1.$\ \hat{j}\times\hat{k}.$ }\)
\(\text{2.$\ \hat{i}\times4\hat{i}$ .}\)
\(\text{3.$\ \left(2\hat{i}+3\hat{j}-\hat{k}\right)\times\left(3\hat{j}+2\hat{k}\right).$ }\)
\(\text{4.$\ 3\hat{j}\times5\hat{i}$ . }\)
\(\text{5.$\ \left(\hat{i}-3\hat{j}+\hat{k}\right)\times\left(2\hat{i}+\hat{j}-\hat{k}\right).$ }\)
\(\text{1.$\ \hat{i}\quad\text{2.$\ \hat{0}\quad\text{3.$\ 9\hat{i}-4\hat{j}+6\hat{k}\quad\text{$4.\ -15\hat{k}\quad\text{5.$\ \left(2\hat{i}+3\hat{j}+7\hat{k}\right).$ }$ }$ }$ }$ }\)
Exercise 2
Find a unit vector perpendicular to both \(\left(\vec{i}-\vec{k}\right)\) and \(\left(\vec{i}+3\vec{j}-2\vec{k}\right)\).
\(\frac{\left(3,1,3\right)}{\sqrt{19}}\text{ or $-\frac{\left(3,1,3\right)}{\sqrt{19}}$ }\).
Download this page, V4 Vector product (PDF 842 KB)
What's next... V5 Projection of vectors
