Learning Lab

Vectors and Scalars

One example of a vector is velocity . The velocity of an object is determined by the magnitude (speed) and direction of travel. Other examples of vectors are force, displacement and acceleration.

A scalar is a quantity that has magnitude only. Mass, time and volume are all examples of scalar quantities.

Vectors in three-dimensional space are defined by three mutually perpendicular directions and and can be denoted as bold letters or as in this worksheet \(\vec{a}\) or \(\vec{b}\) or \(\vec{c}.\)

A vector in the opposite direction from \(\vec{a}\) is denoted by \(-\vec{a}\).

Vectors can be added or subtracted graphically using the triangle rule.

Adding and Subtracting Vectors

Triangle Rule:

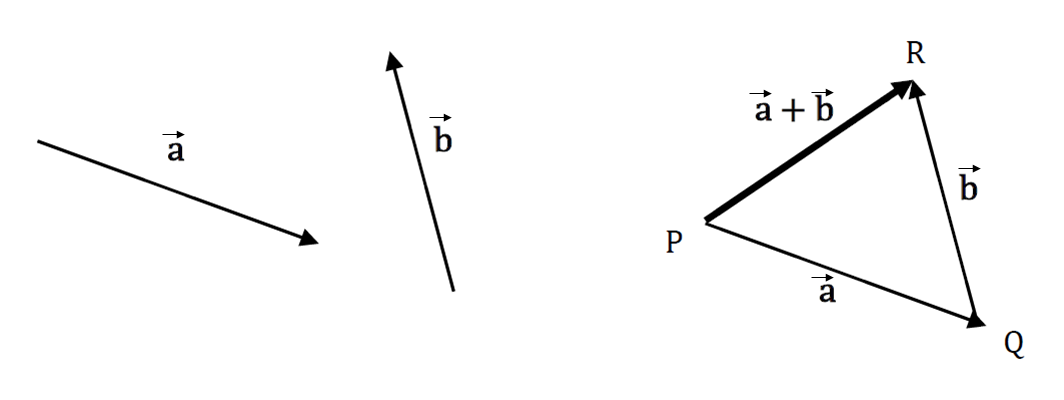
To add vectors \(\vec{a}\) and \(\vec{b}\) shown above place the tail of vector \(\vec{b}\) at the head of vector \(\vec{a}\) (point Q).

The vector sum, \(\vec{a}+\vec{b},\) is the vector \(\overrightarrow{PR}\) , from the tail of vector \(\vec{a}\) to the head of \(\vec{b}.\)

To subtract \(\vec{b}\) from \(\vec{a}\), reverse the direction of \(\vec{b}\) to give \(-\vec{b}\) then add \(\vec{a}\) and \(-\vec{b}\).

\(\vec{a}-\vec{b}=\vec{a}+(-\vec{b})\)

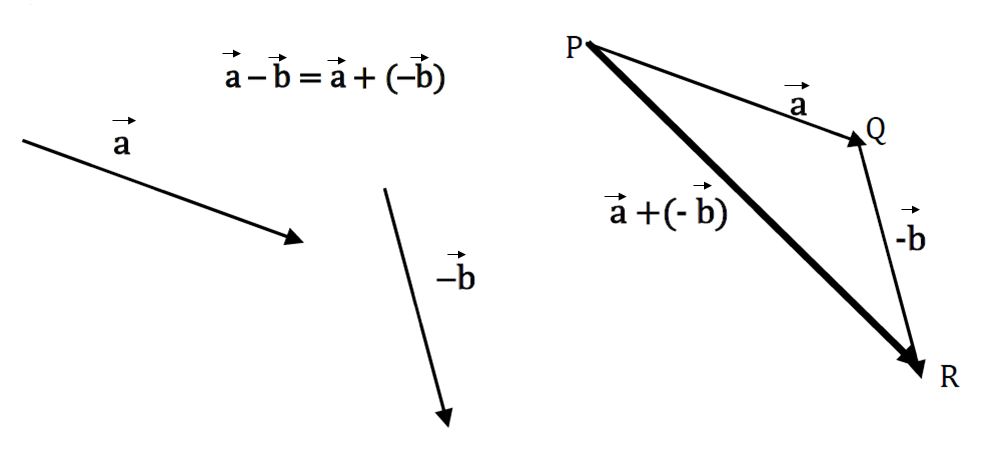
Vector \(\overrightarrow{PR}\) is equal to the vector \(\vec{a}-\vec{b}\).

Components of a Vector

In the diagram below the vector \(\vec{r}\) is represented by \(\overrightarrow{OP}\) where \(P\) is the point \((x,y,z)\).

if \(\vec{i}\) ,\(\vec{j}\) , and \(\vec{k}\) are vectors of magnitude one11 A vector of magnitude one is called a unit vector. Magnitude of vectors and unit vectors are discussed later in this module. parallel to the positive directions of the \(x\)- axis , \(y\)-axis and \(z\)-axis respectively, then:

\(x\vec{i}\) is a vector of length x in the direction of the \(x\)-axis

\(y\vec{i}\) is a vector of length y in the direction of the \(y\)-axis

\(z\vec{k}\) is a vector of length z in the direction of the \(z\)-axis

\(\overrightarrow{OP}\) is then the vector \(x\vec{i}+y\vec{j}+z\vec{k}\)

\(x\), \(y\) and \(z\) are called the components of the vector.

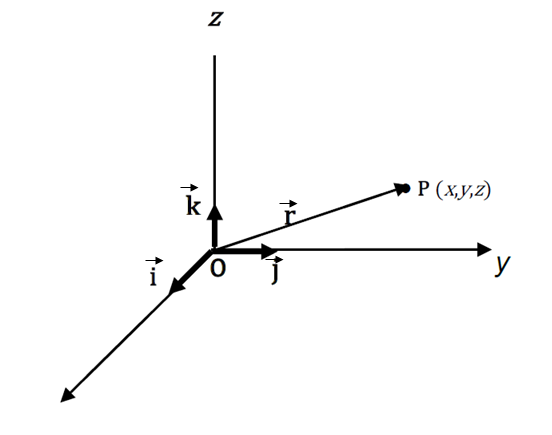
The notation \((x,y,z)\) will be used to denote the vector \(\vec{r}=(x\vec{i}+y\vec{j}+z\vec{k})\) as well as the co-ordinates of a point \(P\) \((x,y,z)\). The context will determine the correct meaning.

Vectors may also be added or subtracted by adding or subtracting their corresponding components.

Directed Line Segment

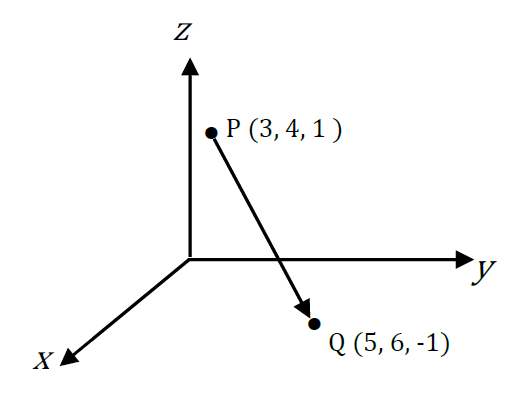
The directed line segment, or geometric vector, \(\overrightarrow{PQ}\) , from\(P(x_{1},y_{1},z_{1})\) to \(Q(x_{2},y_{2},z_{2})\) is found by subtracting the co-ordinates of \(P\) (the initial point) from the co-ordinates of \(Q\) (the final point).

\(\overrightarrow{PQ}=(x_{2}-x_{1})\vec{i}+(y_{2}-y_{1})\vec{j}+(z_{2}-z_{1})\vec{k}\)

Position Vector

The position vector of any point is the directed line segment from the origin \(O\) \((0,0,0)\) to that point and is given by the co-ordinates of of the point.

The position vector of \(P(3,4,1)\) is \(3\vec{i}+4\vec{j}+\vec{k}\), or \((3,4,1)\).

See Exercise 2.

Magnitude of a vector

if \(\vec{a}=a_{1}\vec{i}+a_{2}\vec{j}+a_{3}\vec{k}\) the length or magnitude of \(\vec{a}\) is written as \(\left|\vec{a}\right|\) or \('\vec{a}'\) and is evaluated as:

\(\left|\vec{a}\right|=\sqrt{(a_{1})^{2}+(a_{2})^{2}+(a_{3})^{2}}\)

Unit Vector

Any vector with a magnitude of one is called a unit vector.

If \(\vec{a}\) is any vector then a unit vector parallel to \(\vec{a}\) is written \(\hat{a}\) (a “hat”). The “hat” symbolises a unit vector.

The unit vector \(\hat{a}\) equals vector \(\vec{a}\) divided by its magnitude \(\left|\vec{a}\right|\) .

\[\begin{alignat*}{1} \hat{a} & =\frac{\vec{a}}{\left|\vec{a}\right|}\\ Rearanging\ & \ gives\\ \vec{a} & =\left|\vec{a}\right|\hat{a} \end{alignat*}\]

Of particular importance are unit vectors \(\vec{i}\), \(\vec{j}\) and \(\vec{k}\), parallel to the \(x\) , \(y\), and \(z\) axes respectively.

Multiplication by a Scalar

To multiply a vector \(\vec{a}=\) \(a_{1}\vec{i}+a_{2}\vec{j}+a_{3}\vec{k}\) by a scalar, \(m\), multiply each component of \(\vec{a}\) by \(m\).

\[\begin{alignat*}{1} m\vec{a} & =ma_{1}\vec{i}+ma_{2}\vec{j}+ma_{3}\vec{k} \end{alignat*}\]

The result is a vector of length \(m\times\left|\vec{a}\right|\)

If \(m>0\) the resultant vector is in the same direction as \(\vec{a}\)

If \(m<0\) the resultant vector is in the opposite direction from \(\vec{a}\).

Two vectors a and b are said to be parallel if and only if \(\vec{a}=k\vec{b}\) where \(k\) is a real constant.

Exercise 1

Given \(\vec{a}=(2,1,1)\) , \(\vec{b}=(1,3,-3)\) and \(\vec{c}=(0,3,-2)\) find:

1. \(\vec{a}+\vec{b}\)
   
2. \(\vec{a}+\vec{c}\)
   
3. \(\vec{c}-\vec{b}\)
   
4. \(\vec{a}-\vec{b}\).

Exercise 2

1. Given the points \(A(3,0,4)\) , \(B(-2,4,3)\), and \(C(1,-5,0)\), find:

\(\text{i}.\;\overrightarrow{AB}\quad\) ii. \(\overrightarrow{AC}\quad\) iii. \(\overrightarrow{CB}\quad\) iv. \(\overrightarrow{BC}\quad\) v. \(\overrightarrow{CA}\)
Compare your answers to (ii) and (v), and also to (iii) and (iv). What do you notice?

2. What are the position vectors of the points \(A,\,B\) and \(C\)?

Exercise 3

1. Find the length of the vectors:
   \(\text{(i)}\;(3,-1,-1)\quad\) (ii) \((0,2,4)\quad\) (iii) \((0,-2,0)\)

2. Given the points \(A\,(3,0,4)\), \(B\,(0,4,3)\) and \(C\,(1,-5,0)\);
   find unit vectors parallel to \(\text{(i)}\;\overrightarrow{BA}\quad\text{(ii) $\overrightarrow{CB}\quad\text{(iii) $\overrightarrow{AC}$ .}$ }\)

Exercise 4

1. Expand the following: (i) \(3(\vec{i}+3\vec{j}-5\vec{k})\) (ii) \(-4(\vec{j}-3\vec{k})\)

2. If \(\vec{a}=(2,-2,1)\) , \(\vec{b}=(0,1,1)\) and \(\vec{c}=(-1,3,-2)\) , find (i) \((2\vec{a}+3\vec{b})\) (ii) \((3\vec{a}-2\vec{b})\) (iii) \((2\vec{a}-\vec{b}+2\vec{c})\) (iv) a unit vector parallel to \(2\vec{a}-\vec{b}\)

3. Write down a vector three times the length of \((6\vec{i}+2\vec{j}-5\vec{k})\) and in the opposite direction.