V10 Distance from a point to a plane

Open image

The shortest distance from some point in the air down to flat ground, is defined by a line straight down, sitting at right angles to the ground.

Learn how to find the perpendicular (right angle) distance from a point to a plane.

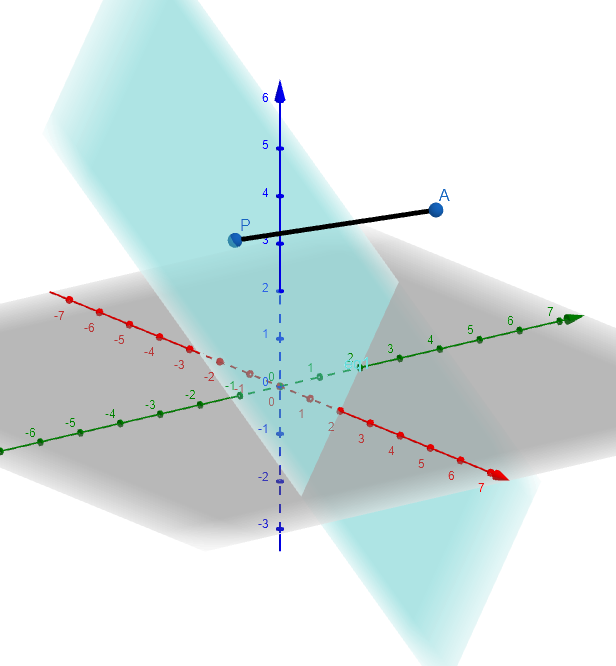
What do we mean when we talk about distance from a point to a plane? Consider the figure below. Here the \(x-\)axis is in red, the \(y-\)axis is in green and the \(z-\)axis is in blue. The grey plane is the \(x-y\) plane, it extends in all directions. The aqua plane also extends in all directions.

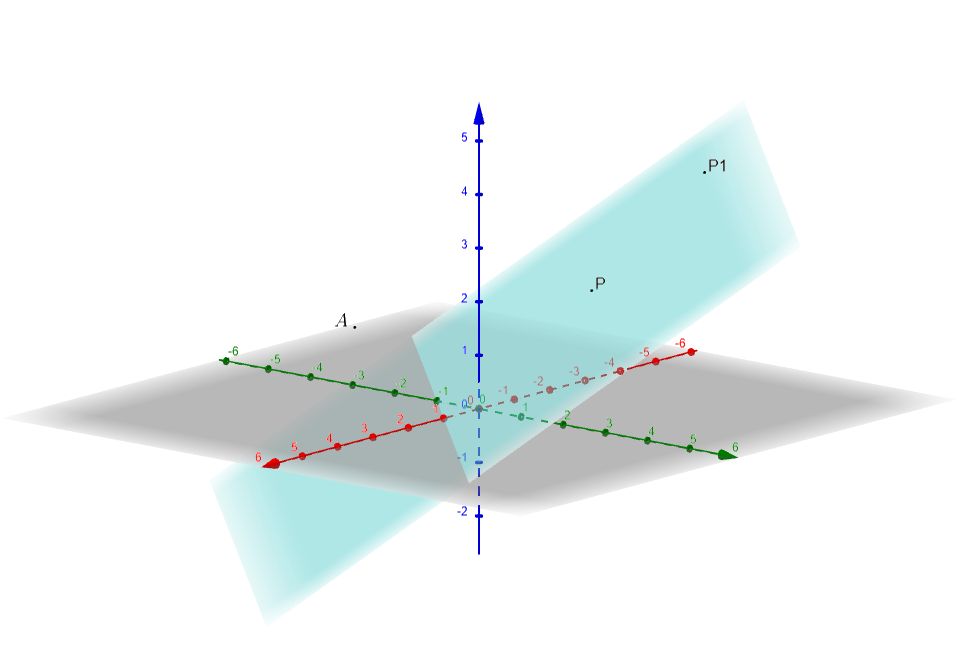
You can have any number of distances from a point \(A\) to the aqua colored plane. For example, the distance from point \(A\) to point \(P\) is one possible answer while the distance from point \(A\) to point \(P1\) is another. This makes no sense. The only interpretation of the question that provides a unique answer is “Find the shortest distance from a point to a plane”. This means we want to find the perpendicular distance from the point to the plane.

When you are asked to find the distance from a point to a plane, you must find the shortest distance from a point to the plane.

Shortest Distance from a Point to a Plane

Consider the figure below. Here, the axes are exactly the same as the figure above. To find the shortest distance from a point \(A\) to the aqua colored plane we first choose any point on the plane \(P\) as shown below. Now define a vector from \(P\) to \(A\), \(\overrightarrow{PA}\). The shortest distance \(d\) is then11 This is sometimes called the scalar resolute of \(\overrightarrow{PA}\) in the direction of \(\hat{n}\). Since the unit vector \[\begin{align*} \hat{n} & =\frac{\vec{n}}{\left|\vec{n}\right|} \end{align*}\] we can express the distance as \[\begin{align*} d= & \overrightarrow{PA}\cdot\hat{n}\\ = & \overrightarrow{PA}\cdot\frac{\vec{n}}{\left|\vec{n}\right|}. \end{align*}\] \[\begin{align*} d & =\overrightarrow{PA}\cdot\hat{n} & \left(1\right) \end{align*}\] where \(\hat{n}\) is a unit normal to the plane.

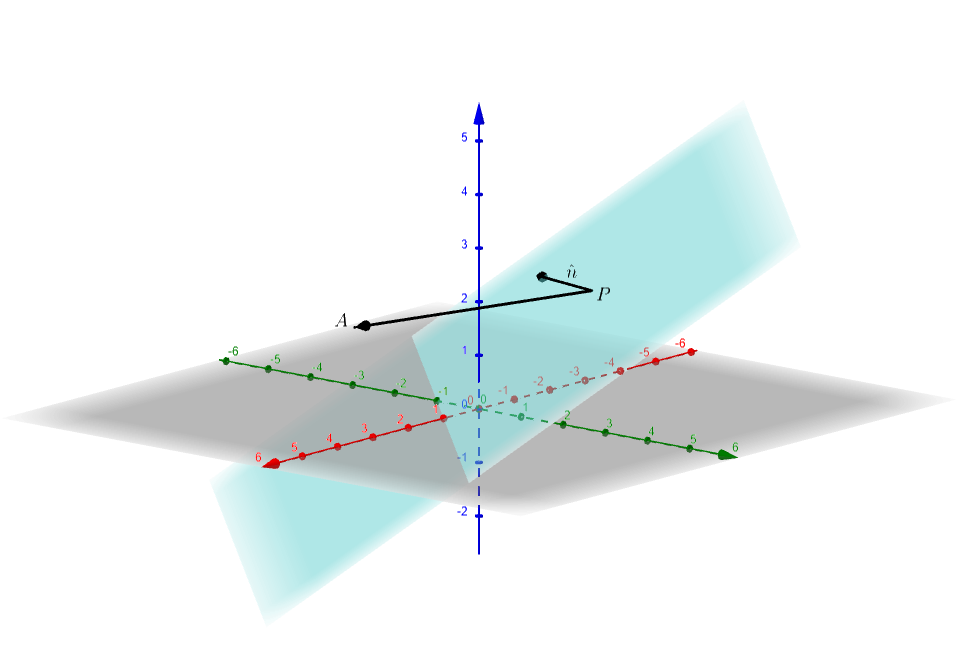
This may be easier to understand if we rotate the picture above so that we view the aqua plane “edge on” as shown below.22 Note that if we take this viewpoint, the distance \(d\) does not change as we rotate the plane about the unit normal vector. This means the perpendicular distance \(d\) does not depend on how you view the problem.

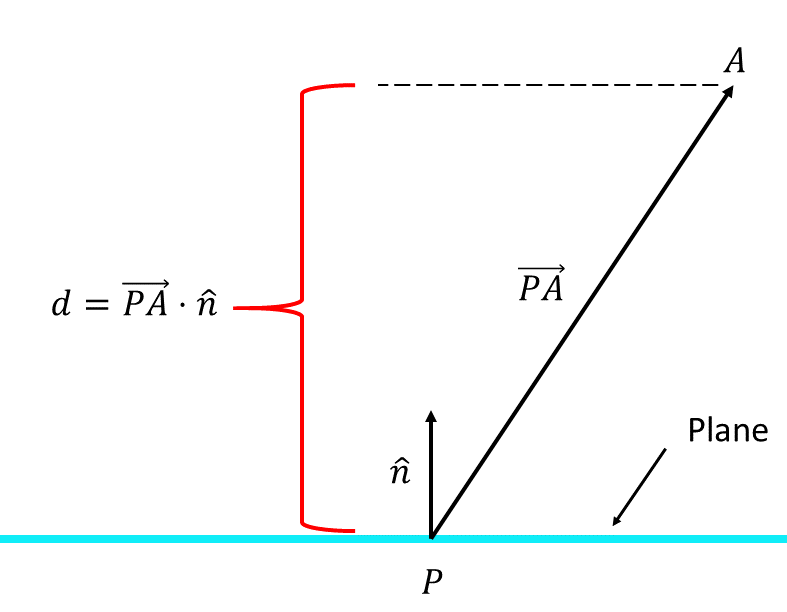
The distance \(d\) is often referred to as the scalar resolute of \(\overrightarrow{PA}\) in the direction of \(\vec{n}.\)

Unit Normal to a Plane

To get the distance from a plane to a point, we need to get a unit normal to the plane. For a plane \[\begin{align*} ax+by+cz & =d \end{align*}\] a normal vector is \(a\hat{i}+b\hat{j+}c\hat{k}.\) For example, the plane \[\begin{align*} 2x+3y-6z & =20 \end{align*}\] has a normal \[\begin{align*} \vec{n} & =2\hat{i}+3\hat{j}-6\hat{k}. \end{align*}\] To create a unit normal \(\hat{n}\) we divide the normal \(\vec{n}\) by it’s length \(\left|\vec{n}\right|\), 33 The length of a vector \(\vec{n}=n_{1}\hat{i}+n_{2}\hat{j}+n_{3}\hat{k}\) is denoted \(\left|\vec{n}\right|\) and \[\begin{align*} \left|\vec{n}\right| & =\sqrt{n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}. \end{align*}\] \[\begin{align*} \left|\vec{n}\right| & =\sqrt{n_{1}^{2}+n_{2}^{2}+n_{3}^{2}}\\ & =\sqrt{2^{2}+3^{2}+\left(-6\right)^{2}}\\ & =\sqrt{49}\\ & =7. \end{align*}\] So a unit normal to the plane is \[\begin{align*} \hat{n} & =\frac{\vec{n}}{\left|\vec{n}\right|}\\ & =\frac{1}{7}\left(2\hat{i}+3\hat{j}-6\hat{k}\right) \end{align*}\]

Example

Find the distance from the point \(\left(2,5,4\right)\) to the plane \(x+2y+2z=2.\)

Solution:

Let point \(A=\left(2,5,4\right)\). Now find a point on the plane.44 It can be ANY point. So to make it easy, we can take \(y=z=0.\) Substituting in the equation for the plane we get \(x=2.\) So the point \(P=\left(2,0,0\right)\) is on the plane. We take \(P=\left(2,0,0\right)\). The vector from \(P\) to \(A\) is \[\begin{align*} \overrightarrow{PA} & =2\hat{i}+5\hat{j}+4\hat{k}-\left(2\hat{i}+0\hat{j}+0\hat{k}\right)\\ & =5\hat{j}+4\hat{k}. \end{align*}\] We now need to find a unit vector that is normal to the plane. A normal vector is \[\begin{align*} \vec{n} & =\hat{i}+2\hat{j}+2\hat{k}. \end{align*}\] A unit normal vector is \[\begin{align*} \hat{n} & =\frac{\vec{n}}{\left|\vec{n}\right|}\\ & =\frac{\hat{i}+2\hat{j}+2\hat{k}}{\sqrt{1^{2}+2^{2}+2^{2}}}\\ & =\frac{\hat{i}+2\hat{j}+2\hat{k}}{\sqrt{9}}\\ & =\frac{1}{3}\left(\hat{i}+2\hat{j}+2\hat{k}\right). \end{align*}\] Using \(\left(1\right)\) above, the distance \(d,\) from \(A=\left(2,5,4\right)\) to the plane \[ x+2y+2z=2 \] is \[\begin{align*} d & =\overrightarrow{PA}\cdot\hat{n}\\ & =\left(5\hat{j}+4\hat{k}\right)\cdot\frac{1}{3}\left(\hat{i}+2\hat{j}+2\hat{k}\right)\\ & =\frac{1}{3}\left(10+8\right)\\ & =6. \end{align*}\]