T2 Right triangle trigonometry
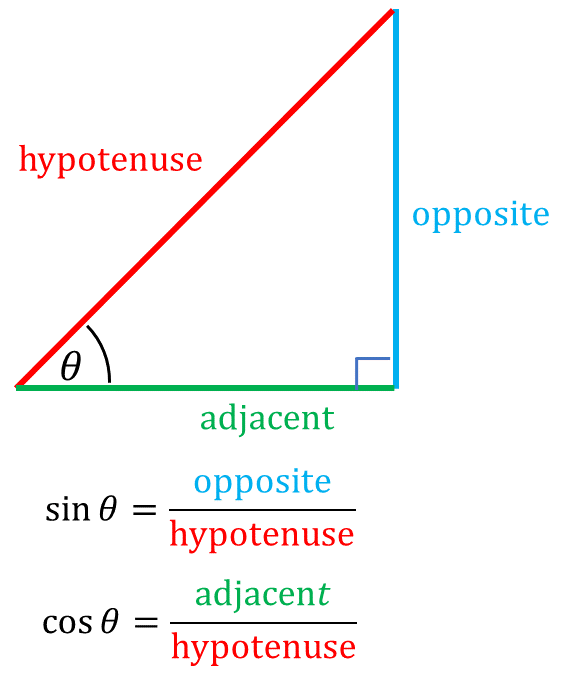
Sine, cos and tan can be defined using side lengths of a right-angled triangle. These side lengths are identified as either the hypotenuse or the opposite or adjacent sides to the angle.
This module shows how to apply trigonometric ratios to find a missing side length, or angle, in a right-angled triangle.
Trigonometry is a branch of mathematics involving the study of triangles, and has applications in fields such as engineering, surveying, navigation, optics, and electronics. The ability to use and manipulate trigonometric functions is necessary in other branches of mathematics, including calculus, vectors and complex numbers.
Right-angled Triangles
A right angle is formed when two lines meet at an angle of \(90^{\circ}.\) Usually a right angle is shown by the symbol shown below.
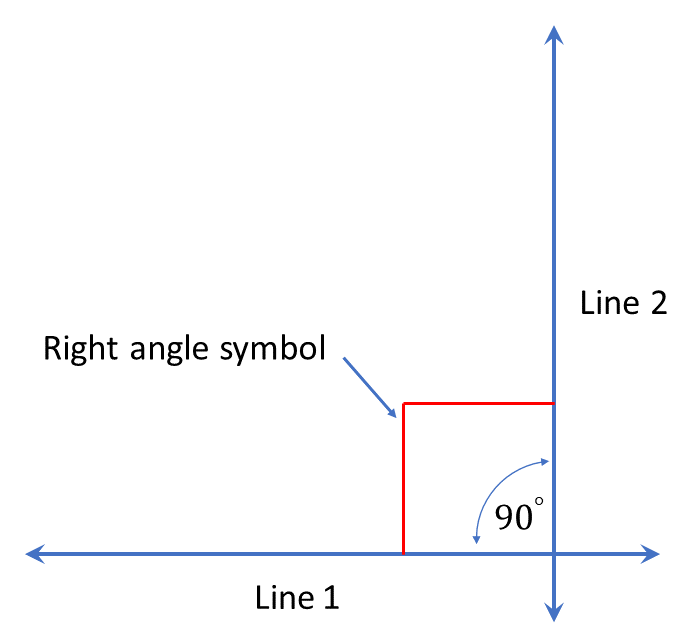
A right-angled triangle is any triangle that contains a right angle.
In a right-angled triangle the three sides are given special names.
The side opposite the right angle is called the hypotenuse (h) – this is always the longest side of the triangle.
The other two sides are named in relation to another known angle (or an unknown angle under consideration).
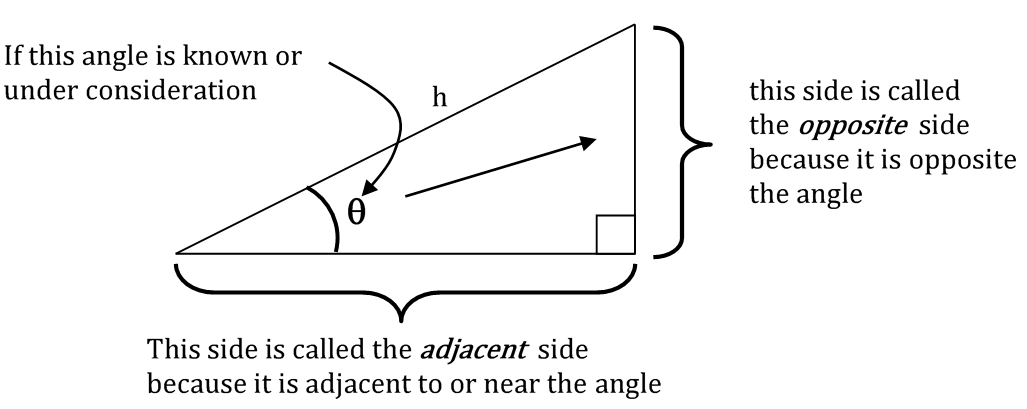
Trigonometric Ratios
In a right-angled triangle the following ratios are defined for a given angle \(\theta\)
\[\begin{align*} sine\,\theta & =\frac{(opposite\;side\;length)}{(hypotenuse\;length)}\\ cosine\,\theta & =\frac{(adjacent\;side\;length)}{(hypotenuse\;length)}\\ tangent\,\theta & =\frac{(opposite\;side\;length)}{(adjacent\;side\;length)} \end{align*}\]
These ratios are abbreviated to \(\sin\theta\), \(\cos\theta\), and \(\tan\theta\) respectively.
A useful memory aid is SOH CAH TOA:
\(\boldsymbol{S}in\,\theta=\frac{\boldsymbol{O}pp}{\boldsymbol{H}yp}\) \(Cos\,\theta=\frac{\boldsymbol{A}dj}{\boldsymbol{H}yp}\) \(\boldsymbol{T}an\,\theta=\frac{\boldsymbol{O}pp}{\boldsymbol{A}dj}\)
These ratios can be used to find unknown sides and angles in right-angled triangles.
Examples
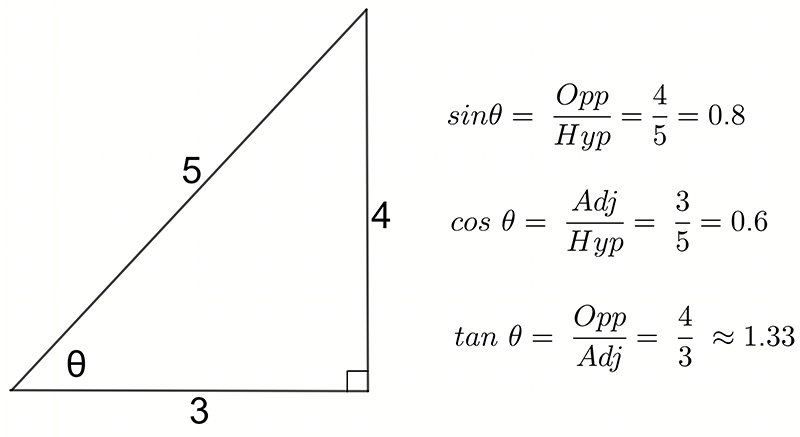
Evaluating Ratios
In the right-angled triangle below evaluate \(sin\,\theta\), \(cos\,\theta\), and \(tan\,\theta\).
Finding Angles
Find the value of the angle in the triangle below1 Step 1: Determine which ratio to use
Step 2: Write the relevant equation
Step 3: Substitute the values
Step 4: Solve the equation
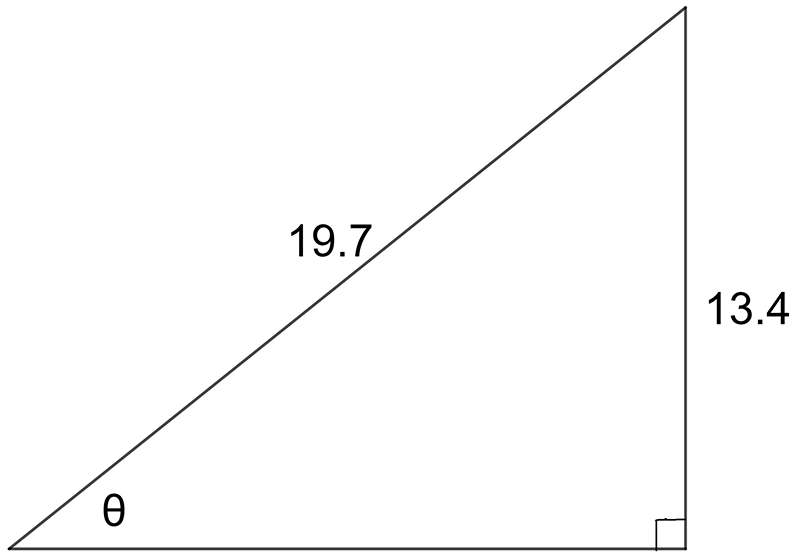
In this triangle we know two sides and need to find the angle .
The known sides are the opposite side and the hypotenuse.
The ratio that relates the opposite side and the hypotenuse is the sine ratio.
\[\begin{align*} \sin\theta & =\frac{Opp}{Hyp}\\ \sin\theta & =\frac{13.4}{19.7}\\ \sin\theta & =0.6802\\ \theta & =\sin^{-1\ }(0.6802)\\ \theta & =42.9^{\circ} \end{align*}\]
Finding Side Lengths
Find the value of the indicated unknown side length in each of the following right-angled triangles.
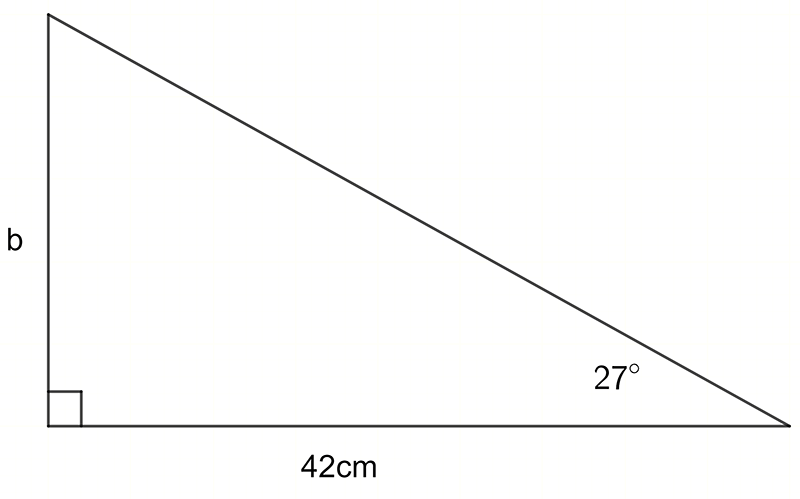
In this problem we know an angle and the adjacent side.
The side to be determined is the opposite side.
The ratio that relates these two sides is the tangent ratio. \[\begin{align*} \tan\theta & =\frac{Opp}{Adj}\\ \tan27^{\circ} & =\frac{b}{42}\\ (\tan27^{\circ})\times42 & =b\\ b & =21.4cm \end{align*}\]
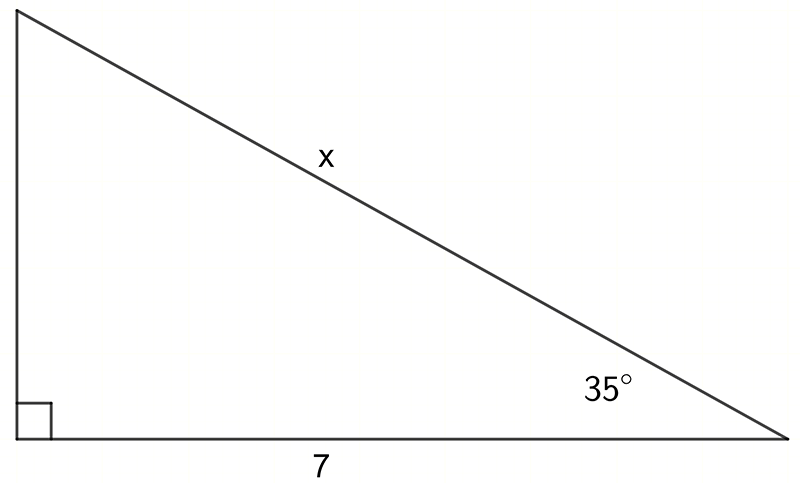
In this problem we know an angle and the adjacent side.
The side to be determined is the hypotenuse.
The ratio that relates these two sides is the cosine ratio.
\[\begin{align*} \cos\theta & =\frac{Adj}{Hyp}\\ \cos35^{\circ} & =\frac{7}{x}\\ (\cos35^{\circ})\times x & =7\\ x & =\frac{7}{\cos35^{\circ}}\\ x & =8.55 \end{align*}\]
Special Angles and Exact Values
There are some special angles for which the trigonometric functions have exact values rather than decimal approximations.2 It is a good idea to remember these values. They occur often in maths courses.
Applying the rules for sine, cosine and tangent to the triangles below, exact values for the sine, cosine and tangent of the angles \(30^{\circ}\), \(45^{\circ}\) and \(60^{\circ}\) can be found.
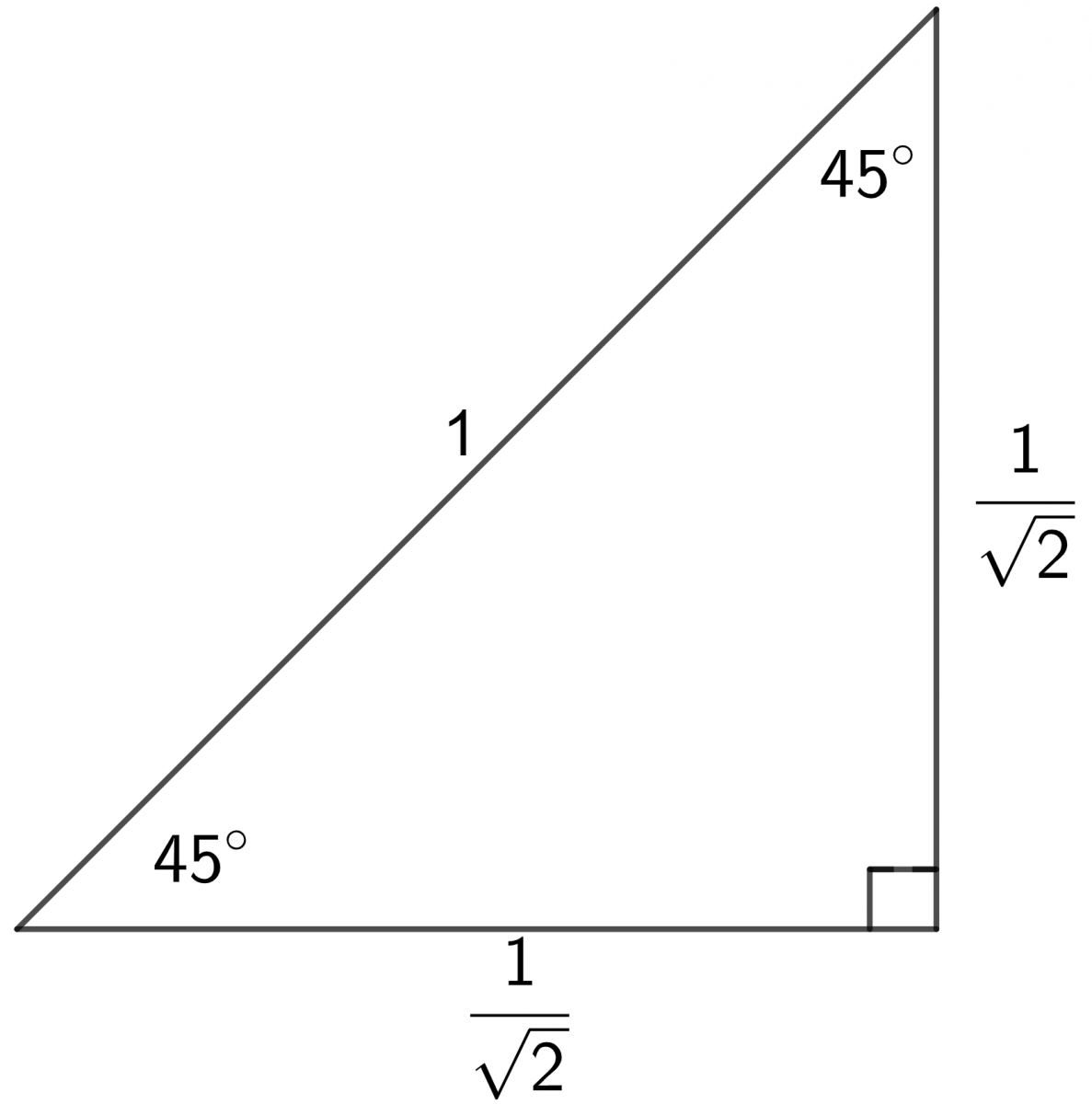
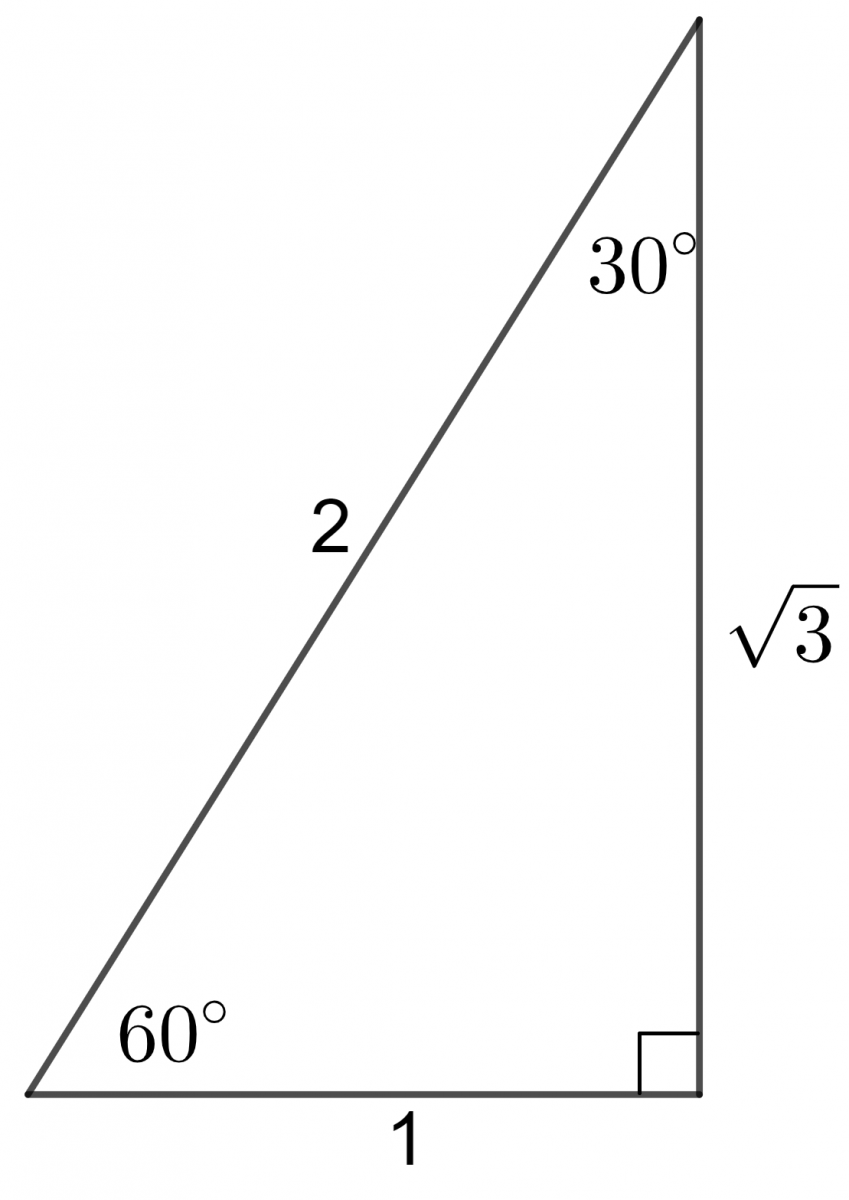
\[\begin{align*} \sin45^{\circ} & =\frac{1}{\sqrt{2}}\qquad\cos45^{\circ}=\frac{1}{\sqrt{2}}\qquad\tan45^{\circ}=1\\ \sin60{}^{\circ} & =\frac{\sqrt{3}}{2}\qquad\cos60^{\circ}=\frac{1}{2}\qquad\tan60^{\circ}=\sqrt{3}\\ \sin30^{\circ} & =\frac{1}{2}\qquad\cos30^{\circ}=\frac{\sqrt{3}}{2}\qquad\tan30^{\circ}=\frac{1}{\sqrt{3}} \end{align*}\]
Exercises
Exercise 1
Using the right-angled triangle below find: (a) \(\sin\theta\), (b) \(\tan\theta\), (c) \(\cos\alpha\), (d) \(\tan\alpha\) (Hint: Use Pythagoras theorem to find the hypotenuse)
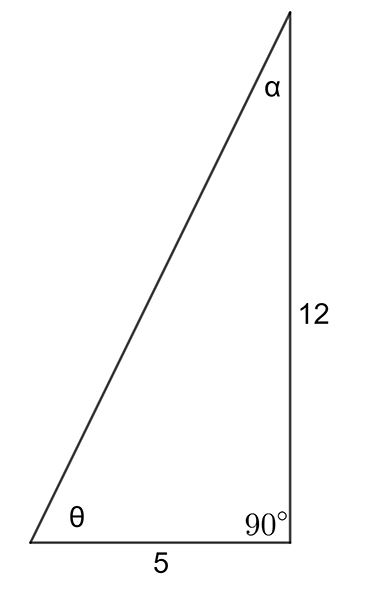
\((\text{a})\;\frac{12}{13}=0.9231\qquad(\text{b})\;\frac{12}{5}=2.4\qquad(\text{c})\;\frac{12}{13}=0.9231\)
\((\text{d})\;\frac{5}{12}=0.4167\).
Exercise 2
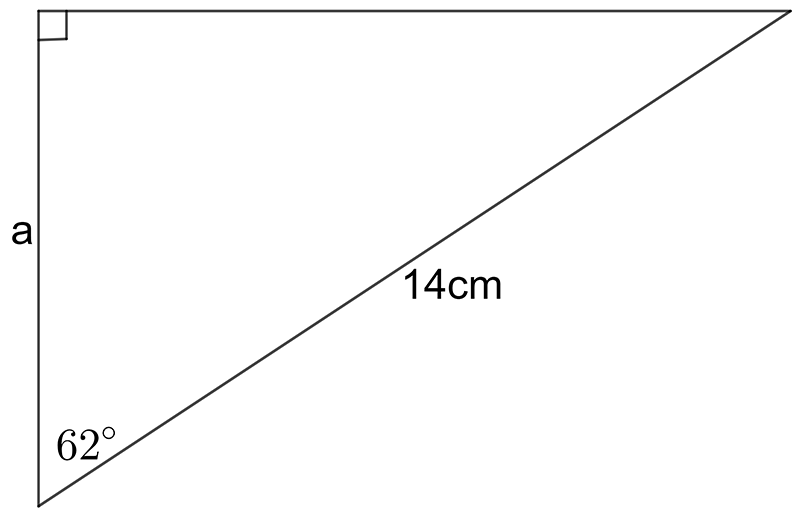
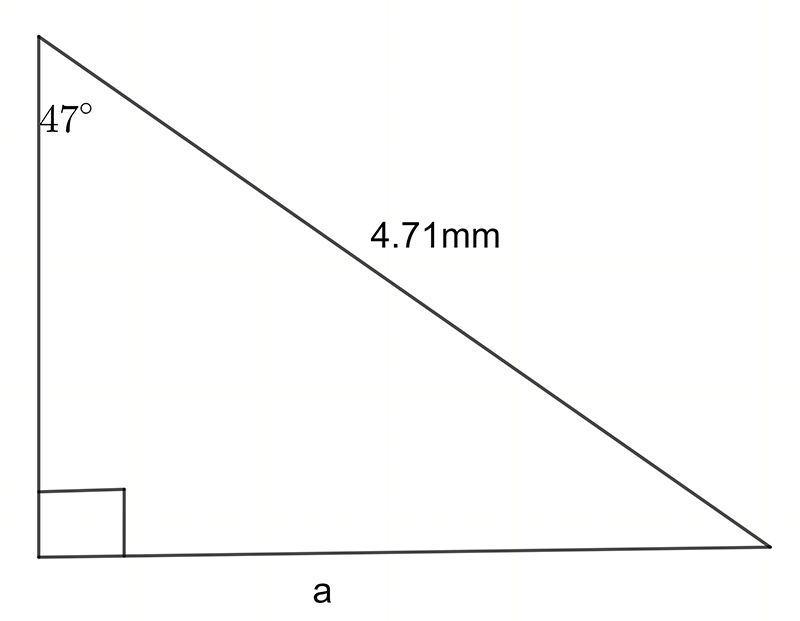
Find the value of the indicated unknown (side length or angle) in each of the following diagrams.
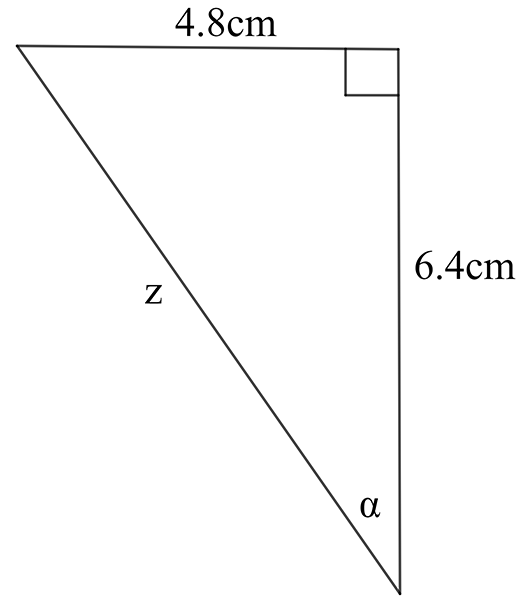
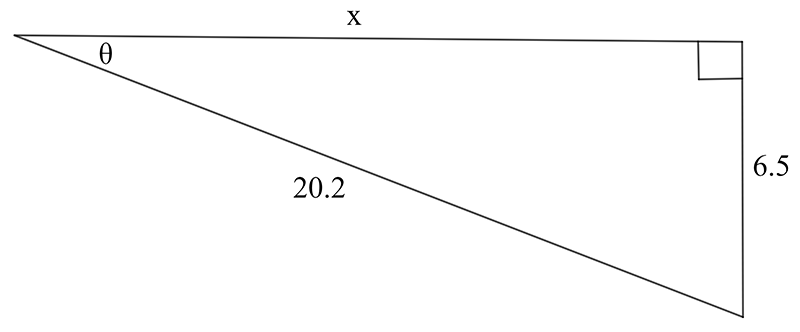
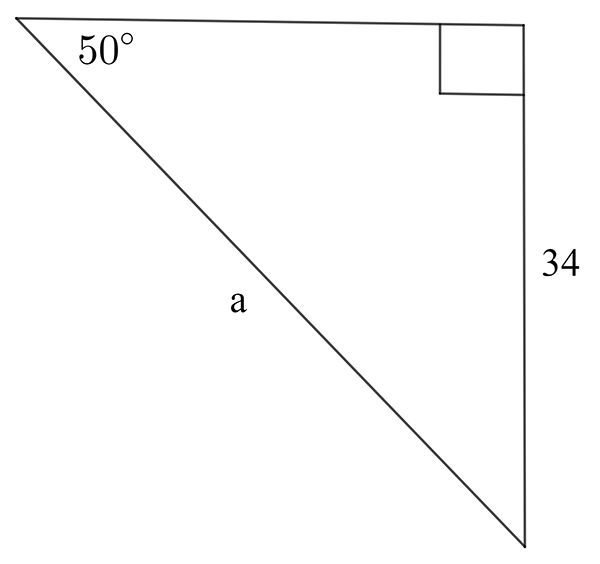
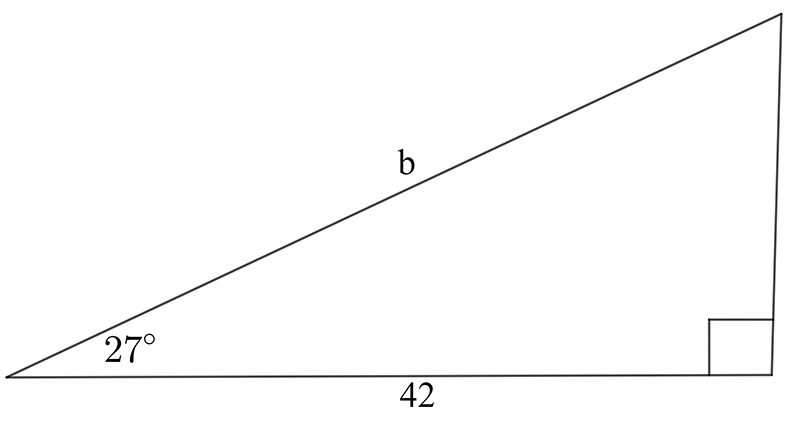
- In a right-angled triangle, \(\sin\phi\) = 0.55 and the hypotenuse is 21mm. Find the length of each of the other two sides.
\((\text{a})\;\text{a}=6.6\,cm\qquad(\text{b})\;\text{a}=3.4\,mm\qquad(\text{c})\;z=7.8\,cm,\,\alpha=37.7^{\circ}\)
\((\text{d})\;\theta=18.8^{\circ},\,x=19.1\qquad(\text{e})\;\text{a}=44.4\qquad(\text{f})\;\text{b}=47.1\)
\((\text{g})\;11.6\,mm\) and \(17.5\,mm.\)
Download this page, T2 Right triangle trigonometry (PDF 1348KB)
What's next... T3 The sine rule
