Skip to content
RMIT University Library - Learning Lab

FG10 (T8) Graphs of sine and cosine functions

 
August 11, 2022 - 2:26pm — AJ (e67821)

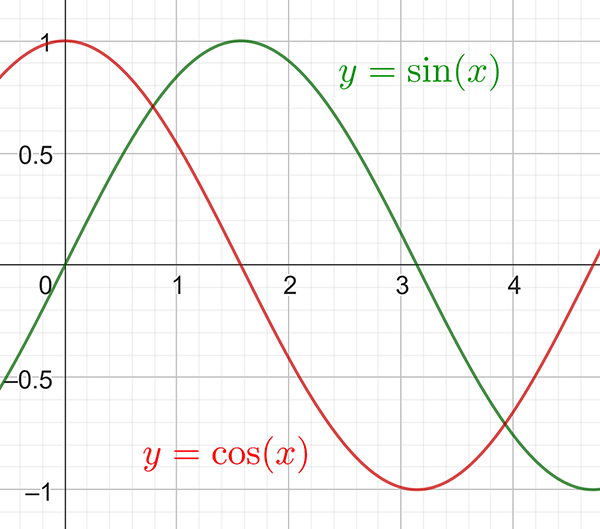
y equals sine x in green and y equals cosine x in red

Both the functions y = sin x and y = cos x have a domain of R and a range of [-1,1]. The graphs of both functions have an amplitude of 1 and a period of 2π radians.

The functions \(y=\sin x\) and \(y=\cos x\) have a domain of \(\mathbb{R}\) and a range of \([-1,1]\).

The graphs of these functions are periodic graphs, that is, the shape of the graph repeats every set period.

The graphs of both functions have an amplitude of \(1\) and a period of \(2\pi\) radians (that is the graph repeats every \(2\pi\) units). They are shown below.

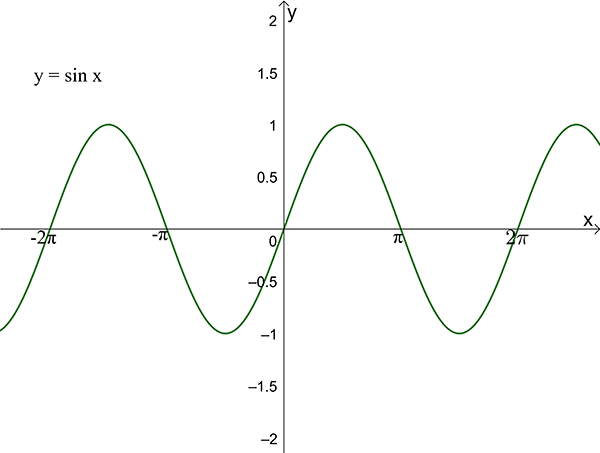
Graph of y equals sine x

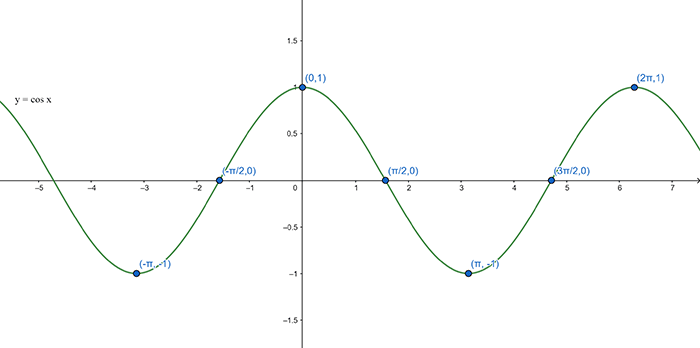
Graph of y equals cosine x

When looking at the graphs remember \(\pi\approx3.142,\) so \(2\pi\approx6.284\).

In this module we look at how the basic graphs may be transformed into graphs of more complex trigonometric functions.

Change of Amplitude and Period

The graphs of both \(y=a\sin nx\) and \(y=a\cos nx\) have an amplitude \(\left|a\right|\) and a period of \(\frac{2\pi}{n}\).

Examples

  1. Graph \(y=3\sin x\).

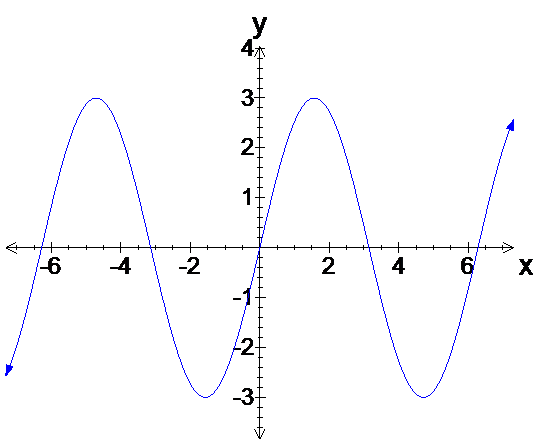
Graph of y equals 3 sine x

In this case, \(a=3\) and \(n=1\), therefore the graph has an amplitude of \(3\) and period of \(2\pi\).

  1. Graph \(y=3\cos2x\).

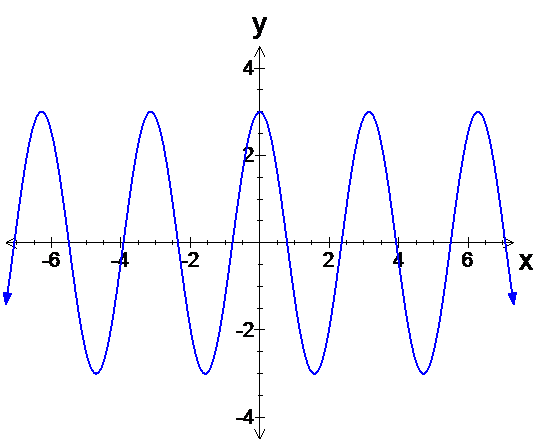
Graph of y equals 3 times sine of two x

In this case, \(a=3\) and \(n=2\), therefore the graph has an amplitude of \(3\) and period of \(\frac{2\pi}{2}=\pi\).

Vertical translation

The graph of \(y=a\sin nx+k\) is the graph of \(y=a\sin nx\) translated up \(k\) units (or down \(k\) units if \(k\) is negative).

The graphs of \({\color{blue}y=\sin x+2}\) and \({\color{red}y=\sin x}\) are shown below.

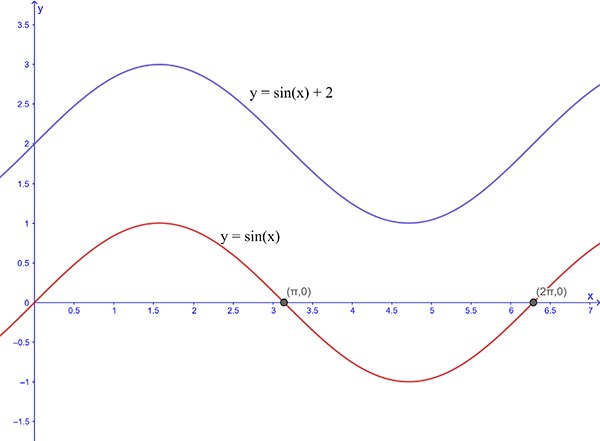
Graph of y equals sine of x plus 2 in blue and y is equal to sine of x in red

Similarly, the graph of \(y=a\cos nx+k\) is the graph of \(y=a\cos nx\) translated up \(k\) units (or down \(k\) units if \(k\) is negative).

Horizontal Translation

Replacing the \(x\) with \(\left(x-\phi\right)\) shifts the graphs of \(y=\sin x\) and \(y=\cos x\) horizontally \(\phi\) units to the right.

Replacing the \(x\) with \(\left(x+\phi\right)\) shifts the graphs of \(y=\sin x\) and \(y=\cos x\) horizontally \(\phi\) units to the left.

Examples

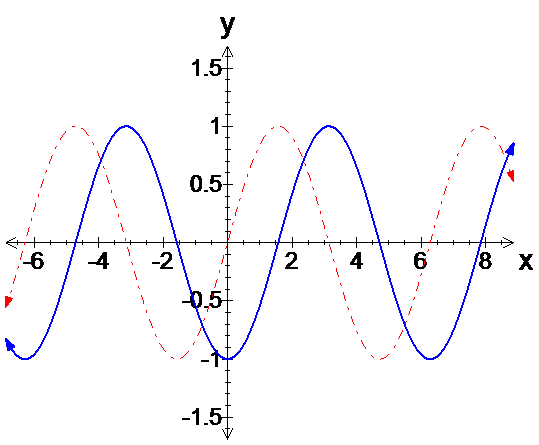
  1. Graph \(y=\sin\left(x-\frac{\pi}{2}\right)\)

The graph of \(y=\sin\left(x-\frac{\pi}{2}\right)\) shown in blue, superimposed on the graph of \(y=\sin x,\) in dashed red is shown below.

Graph of y equals sine x in dashed red superimposed on y equals sine of left bracket x minus pi over 2 right bracket in blue

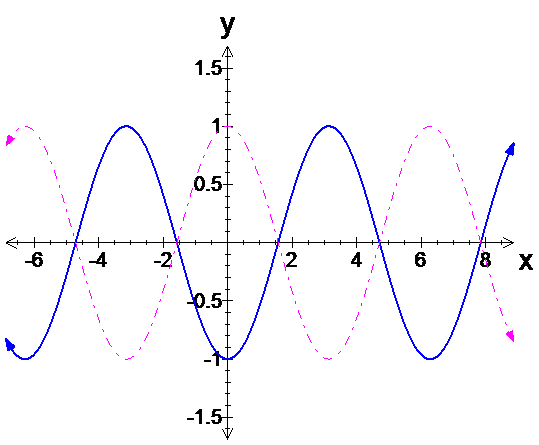
  1. Graph \(y=\cos\left(x+\pi\right)\)

The graph of \(y=\cos\left(x+\pi\right)\), shown in blue, superimposed on the graph of \(y=\cos x\), in dashed red, is shown below.

Graph of y equals cosine x in dashed red superimposed on y equals cosine left bracket x plus pi right bracket in blue

  1. Graph \(y=3\sin\left(4x-\pi\right)\)

1 First change \(y=3\sin\left(4x-\pi\right)\) to the form \(y=3\sin4\left(x-\frac{\pi}{4}\right)\) so that the horizontal translation of the graph is clear.

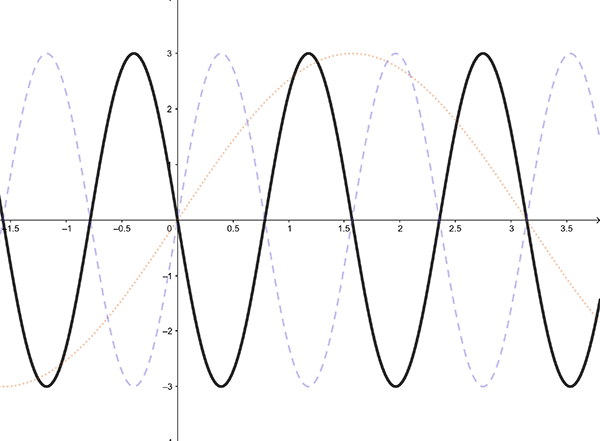
Graph of y equals 3 times sine of 4 times left bracket x minus pi on 4 right bracket in black

The graph of \(y=3\sin4\left(x-\frac{\pi}{4}\right)\) in black is superimposed on the graphs of \(y=3\sin x\) (dotted red) and \(y=3\sin4x\) (dashed grey).

Reflection

Changing the sign of \(a\) in the equations \(y=a\sin nx\) and \(y=a\cos nx\) results in reflection about the \(x\)-axis.

Example

Graph \(y=-3\cos2x\).

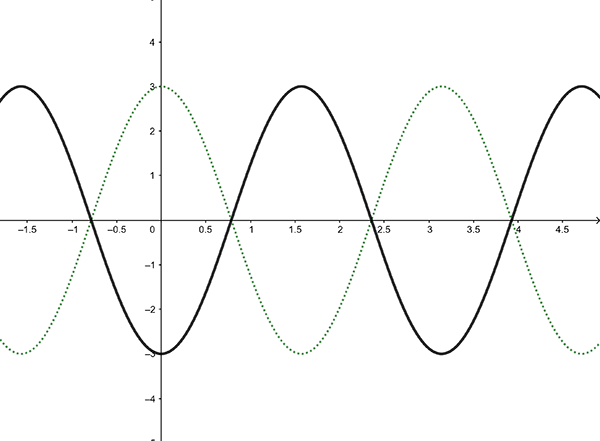
Graph of y equals negative 3 times cosine of 2 times x in black superimposed on y equals 3 times cosine of 2 times x dotted blue

The graph of \(y=-3\cos2x\) (in black) superimposed on the graph of \(y=3\cos2x\) (dotted).

Exercise 1

1. Sketch the graphs of the following functions for one complete cycle stating the amplitude and the period.

(a)\(\,\) \(y=2\cos x\)

(b)\(\,\) \(y=2\sin3x\)

(c)\(\,\) \(y=\frac{1}{2}\sin2x\)

(d)\(\,\) \(y=3\cos\frac{x}{2}\)

(e)\(\,\) \(y=-2\sin3x\)

Answers

1(a)

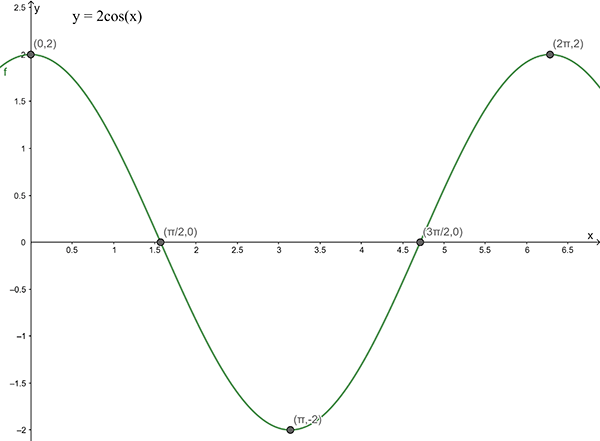
Graph of y equals cosine of left bracket 2 times x right bracket

Amplitude = \(2\) , Period = \(2\pi\)

1(b)

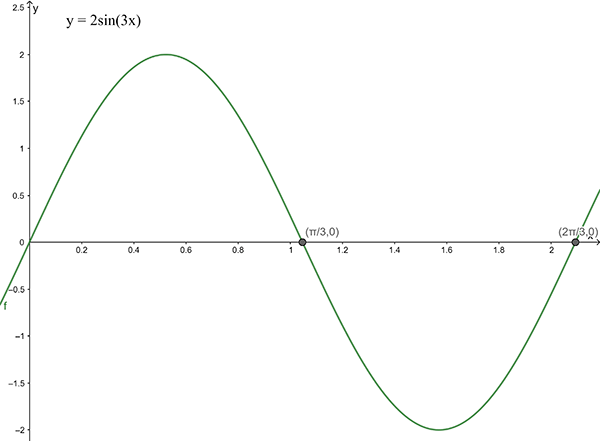
Graph of y equals 2 times sine of ( 3 times x )

Amplitude = \(2\) , Period = \(\dfrac{2\pi}{3}\)

1(c)

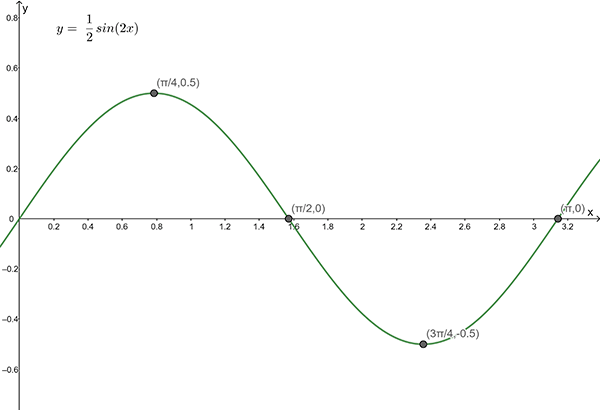
Graph of y equals 0.5 times sine of ( 2 times x )

Amplitude = \(\dfrac{1}{2}\) , Period = \(\pi\)

1(d)

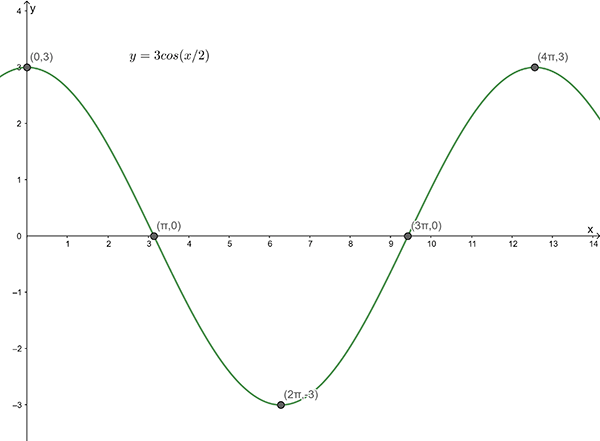
Graph of y equals 3 times the cosine of ( x over 2 )

Amplitude = \(3\) , Period = \(4\) \(\pi\)

1(e)

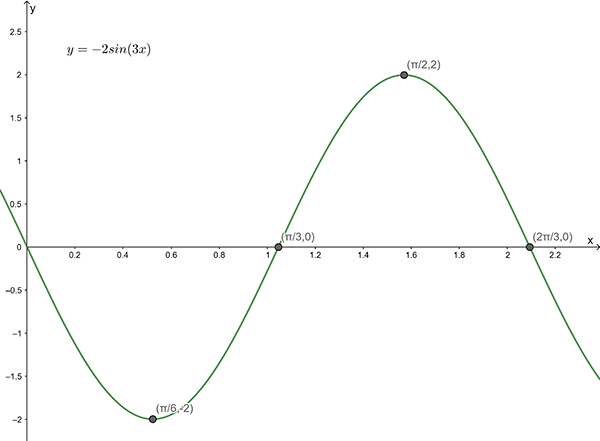
Graph of y equals negative 2 times the sine of ( 3 times x)

Amplitude = \(2\) , Period = \(\dfrac{2\pi}{3}\)

Exercise 2

Sketch the graphs of the following functions for one complete cycle stating the amplitude and period.

  1. \(y=2\sin\left(x-\pi\right)\)

  2. \(y=3\cos\left(x+\frac{\pi}{2}\right)\)

Answers

2(a)

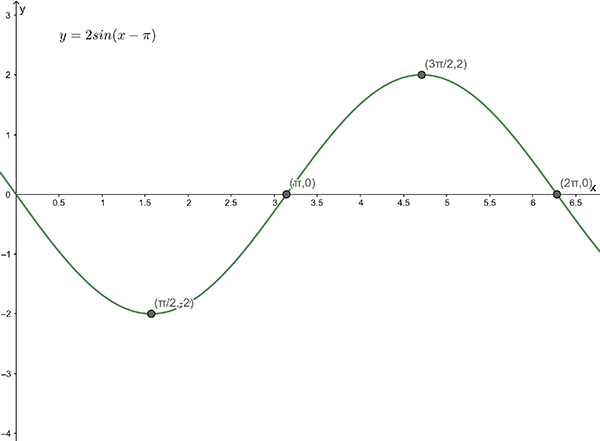
Graph of y equals 2 times the sine of ( x minus pi )

Amplitude = \(2\) , Period = \(2\pi\)

2(b)

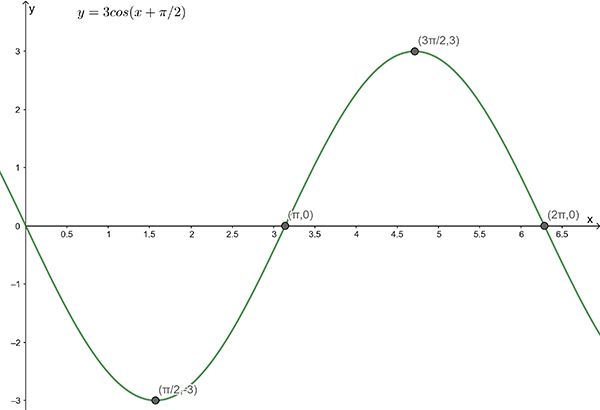
Graph of y equals 3 times the cosine of ( x plus pi divided by 2 )

Amplitude = \(3\) , Period = \(2\pi\)

Exercise 3

Sketch the graphs of the following functions for one complete cycle stating the amplitude and period.

  1. \(y=2\sin\left(3x-\pi\right)\)

  2. \(y=3\cos\left(4x-2\pi\right)\)

  3. \(y=2\sin\left(2x+\frac{\pi}{3}\right)\)

Answers

3(a)

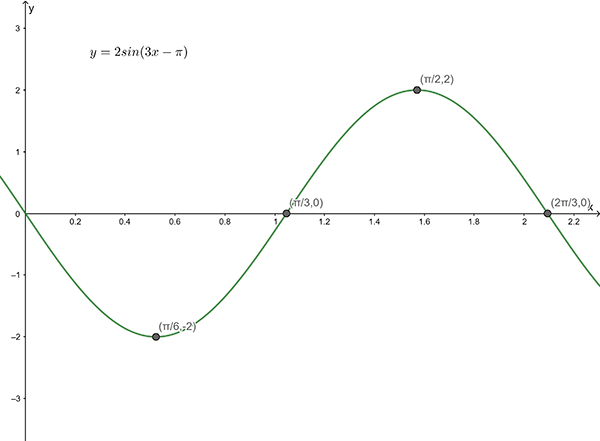
Graph of y equals 2 times the sine of ( 3 times x minus pi )

Amplitude = \(2\) , Period = \(\dfrac{2\pi}{3}\)

3(b)

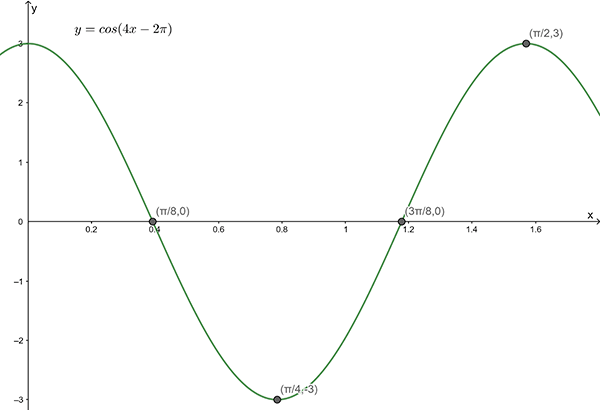
Graph of y equals the cosine of ( 4 times x minus 2 times pi )

Amplitude = \(3\) , Period = \(\dfrac{\pi}{2}\)

3(c)

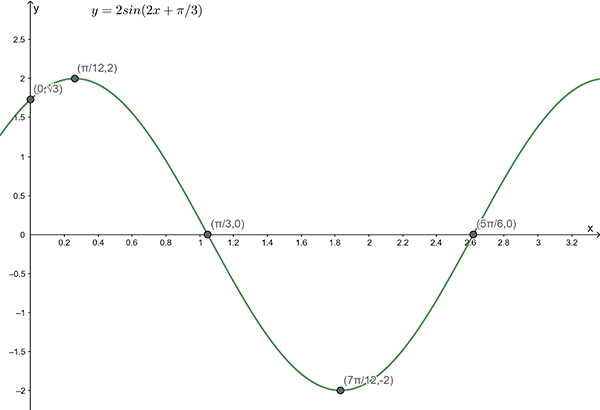
Graph of y equals 2 times the sine of ( 2 times x plus pi divided by 3 )

Amplitude = \(2\) , Period = \(\pi\)

Download this page, FG10 Graphs of Sine and Cosine Functions (PDF 2199KB)

What's next... T9 Trigonometric identities

Keywords: 
Maths
Functions
Graphs