FG6 (T6) Circular functions
The trigonometric ratios that have been defined in right-angled triangles can be extended to angles greater than 90 degrees
Trigonometric functions such as sin, cos and tan are usually defined as the ratios of sides in a right angled triangle. This module defines the trigonometric functions using angles in a unit circle.
The Unit Circle
A unit circle is a circle that is centered at the origin and has a radius of one as shown below. 1 The origin is the point with co-ordinates \(\left(0,0\right)\)
An angle measured from the positive \(x-\) axis maybe used to define any point on the unit circle. Angles may be positive or negative. Positive angles are in an anti-clockwise direction. and negative angles are in a clockwise direction as shown below.
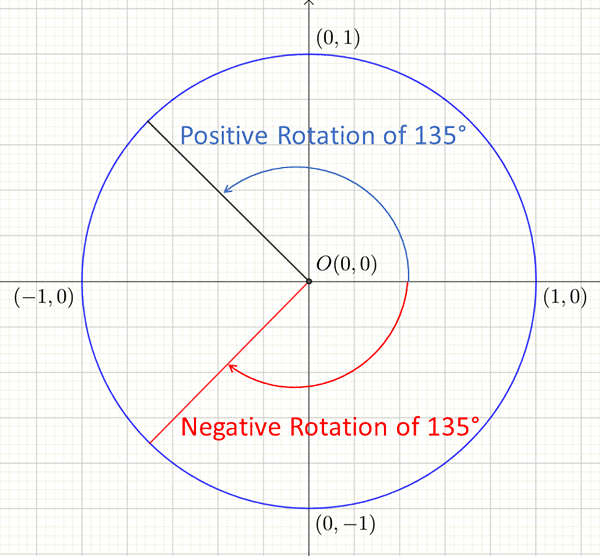
Although there are \(360^{\circ}\) in a circle, it is possible to to rotate through more than \(360^{\circ}\). For example a rotation of \(45^{\circ}\) identifies the same point as a rotation of \(45^{\circ}+360^{\circ}=405^{\circ}\).
Angular Measurement and the Unit Circle
Though angles are often measured in degrees, they may also be measured in radians. One radian is the angle subtended from the \(x-\) axis by an arc whose length is equal to the radius of the circle. In a unit circle , the radius is \(1\). This is illustrated below:
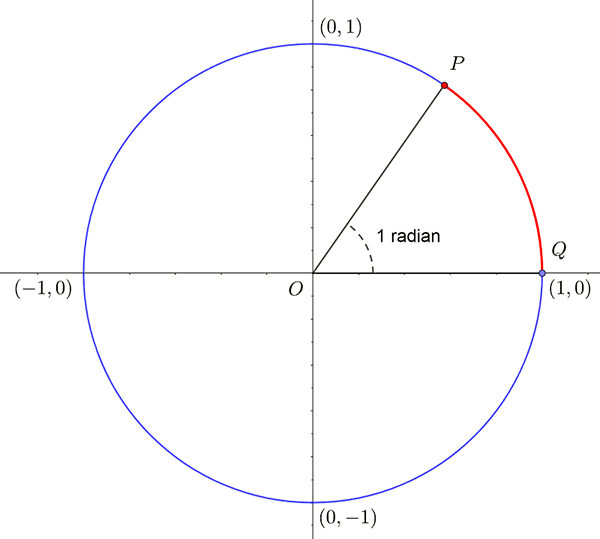
In the figure, the red arc is of length \(1\) and is the same length as the radius. The angle formed is one radian. Radians are abbreviated as rad or a superscript \(c\) like \(^{c}\).
Since the circumference of the unit circle is \(2\pi\) radians
2 The circumference formula is \(C=2\pi r\) where \(r\) is the radius. Since \(r=1\) in a unit circle, we see the circumference is \(2\pi\).
and there are \(360^{\circ}\) in a circle we have \[
360^{\circ}=2\pi\textrm{ rad.}
\]
By dividing the above equation by a number it is possible to derive the following angles in degrees in terms of radians as follows: \[\begin{align*} 30^{\circ} & =\frac{\pi}{6}\\ 45^{\circ} & =\frac{\pi}{4}\\ 60^{\circ} & =\frac{\pi}{3}\\ 90^{\circ} & =\frac{\pi}{2}\\ 180^{\circ} & =\pi\\ 150^{\circ} & =5\times30^{\circ}\\ & =5\times\frac{\pi}{6}\\ & =\frac{5\pi}{6}\\ 270^{\circ} & =3\times90^{\circ}\\ & =3\times\frac{\pi}{2}\\ & =\frac{3\pi}{2}. \end{align*}\] Angles in radians may also be positive and negative. The same convention is used as for degrees, a positive rotation is anti-clockwise and a negative rotation is clockwise.
Sine and Cosine on the Unit Circle
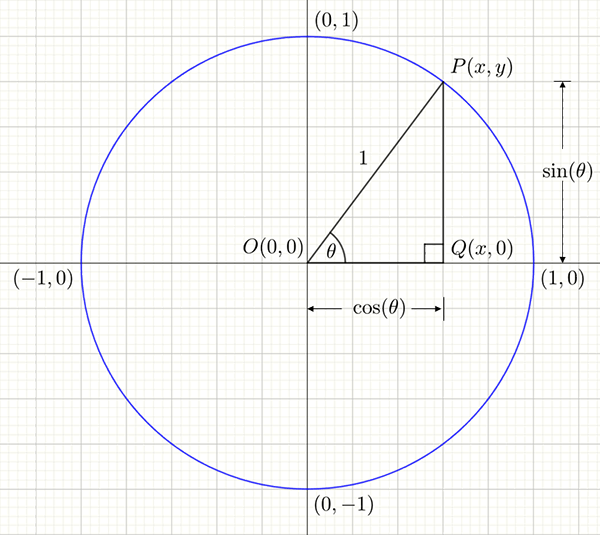
Imagine a point \(P\left(x,y\right)\) on the unit circle as shown below.

In the triangle \(POQ\), the hypotenuse \(OP\) is \(1\), the adjacent side to the angle \(\theta\) is \(OQ\) and the opposite side to the angle \(\theta\) is \(QP\). Using the definitions of sine and cosine in a right angled triangle we get 3 Remember that \[\begin{align*} \cos\theta & =\frac{\textrm{adjacent}}{\textrm{hypotenuse}} \end{align*}\] and \[\begin{align*} \sin\theta & =\frac{\textrm{opposite}}{\textrm{hypotenuse}}. \end{align*}\] \[\begin{align*} \cos\theta & =\frac{\textrm{adjacent}}{\textrm{hypotenuse}}\\ & =\frac{OQ}{OP}\\ & =\frac{x}{1}\\ & =x \end{align*}\] and \[\begin{align*} \sin\theta & =\frac{\textrm{opposite}}{\textrm{hypotenuse}}\\ & =\frac{QP}{OP}\\ & =\frac{y}{1}\\ & =y \end{align*}\]
That is, any point on the unit circle has coordinates \[\begin{align*} x & =\cos\theta\\ y & =\sin\theta \end{align*}\] where \(\theta\) is the angle (positive or negative) measured from the positive \(x-\) axis to the point.
Examples: \(\sin\left(0\right)=0\), \(\ \ \ \ \sin\left(90^{\circ}\right)=\sin\left(\frac{\pi}{2}\right)=1\), \(\ \ \ \ \cos\left(0\right)=1,\) \(\ \ \ \ \cos\left(\frac{\pi}{2}\right)=\) cos\(\left(90^{\circ}\right)=0\).
The Tangent Function
Consider the figure below.
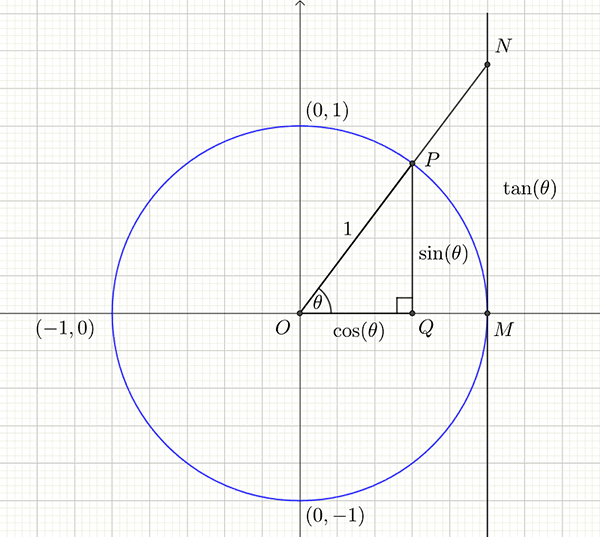
The triangles \(OMN\) and \(OQP\) are similar therefore \[\begin{align*} \frac{MN}{OM} & =\frac{PQ}{OQ}\\ MN & =\frac{PQ}{OQ} & since\ OM=1 \end{align*}\] \(OM=1\) (it is a unit circle). We define the length \(MN\) to be the tangent of the angle \(\theta\) 4 We call this the tangent as it is the distance measured on the vertical tangent to the circle that passes through the point \(\left(1,0\right)\). and abbreviate this to \(\tan\left(\theta\right)\). Also \(\sin\left(\theta\right)=PQ\) and \(\cos\left(\theta\right)=OQ.\) Substituting these relationships into equation \(\left(1\right)\) we have \[\begin{align*} \tan\left(\theta\right) & =\frac{\sin\left(\theta\right)}{\cos\left(\theta\right)}. \end{align*}\] This agrees with the usual definition of tan from right angled trigonometry.
Exact Values of Sine, Cosine and Tangent Functions
To find the value of \(\sin\left(\theta\right),\,\cos\left(\theta\right)\) and \(\tan\left(\theta\right)\) we usually use a scientific calculator. 5 When using the calculator it is essential that it be in degrees or radians mode. However, there are some special angles that are worth remembering. These are shown in the following table.
| Angle \(\left(\theta\right)\) | \(0^{\circ}\) | \(30^{\circ}=\pi/6\) | \(45^{\circ}=\pi/4\) | \(60^{\circ}=\pi/3\) | \(90^{\circ}=\pi/2\) | \(180^{\circ}=\pi\) | \(270^{\circ}=\frac{3\pi}{2}\) |
|---|---|---|---|---|---|---|---|
| \(\sin\) \(\left(\theta\right)\) | \(0\) | \(\frac{1}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{\sqrt{3}}{2}\) | 1 | 0 | -1 |
| \(\cos\) \(\left(\theta\right)\) | \(1\) | \(\frac{\sqrt{3}}{2}\) | \(\frac{1}{\sqrt{2}}\) | \(\frac{1}{2}\) | 0 | -1 | 0 |
| \(\tan\) \(\left(\theta\right)\) | \(0\) | \(\frac{1}{\sqrt{3}}\) | 1 | \(\sqrt{3}\) | undefined | 0 | undefined |
If you know the exact values above, you can work out the exact values for other angles using the symmetry of the unit circle.
Quadrants
The coordinate plane is divided into an upper and lower section by the \(x\)-axis. It is further divided into quadrants by the \(y\)-axis. These four quadrants are numbered from one to four in an anti-clockwise direction as shown below:
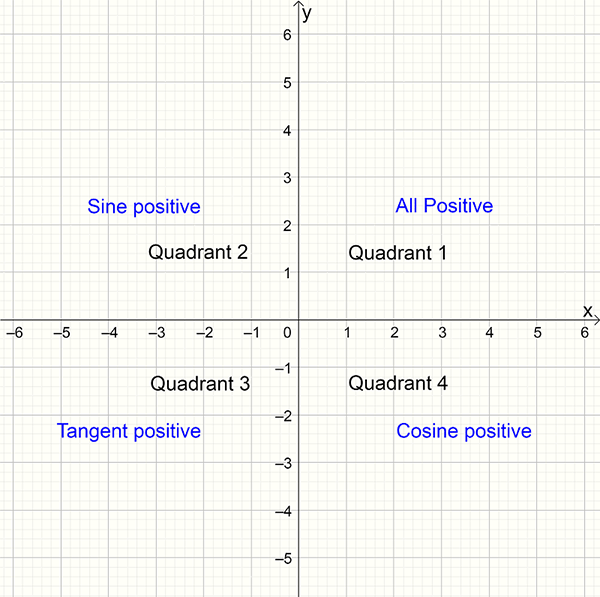
Knowing exact values for some angles in quadrant 1, allows you to find exact values in other quadrants.
Example 1: Find the exact value of \(\sin\left(2\pi/3\right)\) and \(\cos\left(2\pi/3\right)\).
Solution: It is important to make a sketch as shown below. Remember \(\frac{2\pi}{3}=120^{\circ}\).
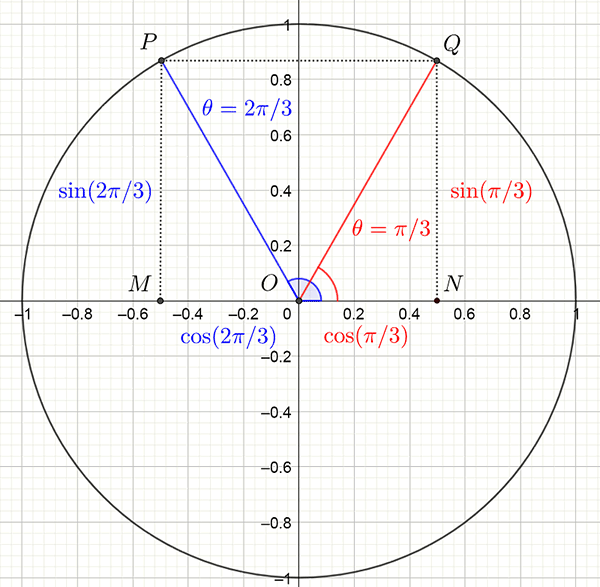
First draw in the angle you are interested in. In this case it is \(2\pi/3\) and is shown in blue as are the required values for the circular functions sin and cos. Now use symmetry of the unit circle about the \(y-\) axis to draw in an angle that is related to \(2\pi/3\) but for which you know the exact value. In this case it is \(\pi/3\) and is shown in red. You can see that the length of \(NQ\) is the same as \(MP\) which means \[\begin{align*} NQ & =MP\\ \sin\left(\frac{2\pi}{3}\right) & =\sin\left(\frac{\pi}{3}\right)\\ & =\frac{\sqrt{3}}{2}\quad\textrm{ from the table.} \end{align*}\]
Now note that the the lengths of \(ON\) and \(MO\) are the same but \(MO=-ON=-\cos\left(\pi/3\right)\) and so \[\begin{align*} \cos\left(\frac{2\pi}{3}\right) & =-ON\\ & =-\cos\left(\pi/3\right)\\ & =-\frac{1}{2}\quad\textrm{ from the table.} \end{align*}\]
Example 2: Find the exact value of \(\sin\left(330^{\circ}\right)\).
Plotting \(330^{\circ}\) on a unit circle shows that \(\sin\left(330^{\circ}\right)\) is closely related to \(\sin\left(30^{\circ}\right).\) The \(y-\)coordinates differ only by sign because the distances from the \(x-\)axis are the same.
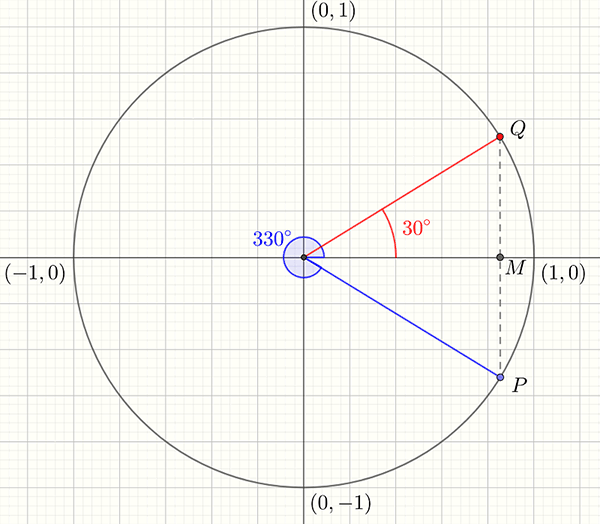
We have \[\begin{align*} MP & =-MQ\\ \sin\left(330^{\circ}\right) & =-\sin\left(30^{\circ}\right)\\ & =-\frac{1}{2}\quad\textrm{ from the table.} \end{align*}\]
Note: \[\begin{align*} \cos\left(330^{\circ}\right) & =\cos\left(360^{\circ}-30^{\circ}\right)\\ & =\cos\left(30^{\circ}\right)\\ & =\frac{\sqrt{3}}{2}\quad\textrm{ from the table.} \end{align*}\]
Example 3: Find the exact value of \(\tan\left(4\pi/3\right)\).
Plotting \(4\pi/3\) on a unit circle shows that \(\tan\left(4\pi/3\right)\) is closely related to \(\tan\left(\pi/3\right)\).
Remember \(\frac{4\pi}{3}=\frac{3\pi}{3}+\frac{\pi}{3}=\pi+\frac{\pi}{3}\)
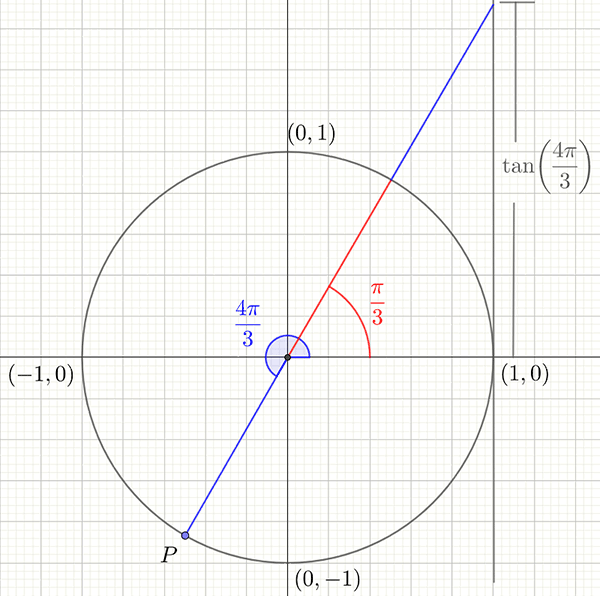
We see that \[\begin{align*} \tan\left(\frac{4\pi}{3}\right) & =\tan\left(\frac{\pi}{3}\right)\\ & =\sqrt{3}\quad\textrm{ from the table.} \end{align*}\]
Exercises
- What are the coordinates for points on the unit circle that make the following angles with the positive \(x-\)axis?
\[\begin{array}{lllll} a)\,30^{\circ} & & b)\,125^{\circ} & & c)\:-60^{\circ}\\ d)\,270^{\circ} & & e)\,-180^{\circ} & & f)\,720^{\circ} \end{array}\]
- Find exact values for:
\[\begin{array}{lllll} a)\,\sin\left(330^{\circ}\right) & & b)\,\cos\left(210^{\circ}\right) & & c)\,\sin\left(-30^{\circ}\right)\\ d)\,\cos\left(90^{\circ}\right) & & e)\,\tan\left(300^{\circ}\right) & & f)\,\cos\left(180^{\circ}\right)\\ g)\,\sin\left(-120^{\circ}\right) & & h)\,\cos\left(315^{\circ}\right) \end{array}\]
\[\begin{array}{llllll} a)\:\left(cos\left(30^{\circ}\right),sin\left(30^{\circ}\right)\right)=\left(0.87,0.5\right)\ \ \ & b)\,\left(-0.56,0.82\right)\ \ \ & c)\,\left(0.5,-0.87\right)\ \ \ & d)\,\left(0,-1\right)\ \ & e)\,\left(-1,0\right)\ \ \ & f)\,\left(1,0\right)\end{array}\]
\[\begin{array}{llllll} a)\,0.5\ \ \ & b)\,\sqrt{3}/2\ \ \ & c)\,-0.5 & \ \ \ d)\,0 & \ \ \ e)\,\sqrt{3} & \ \ \ f)\,-1\\ g)\,-\sqrt{3}/2 & h)\,1/\sqrt{2} \end{array}\]
Download this page, FG6 Circular Functions (PDF 1179KB)
What's next... FG7 Linear graphs or T7 Trigonometric equations
