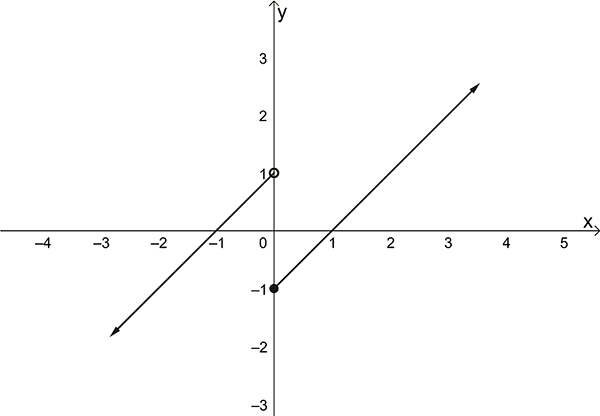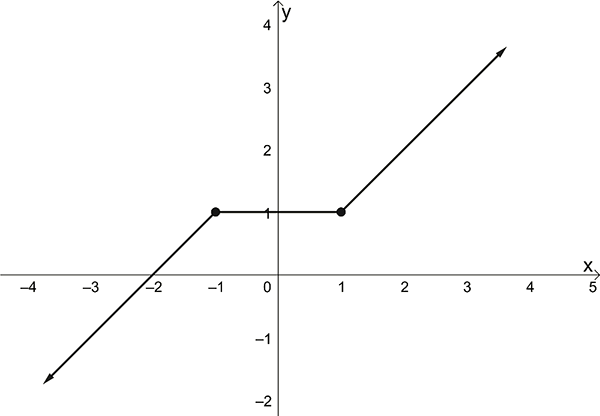FG5 Hybrid functions
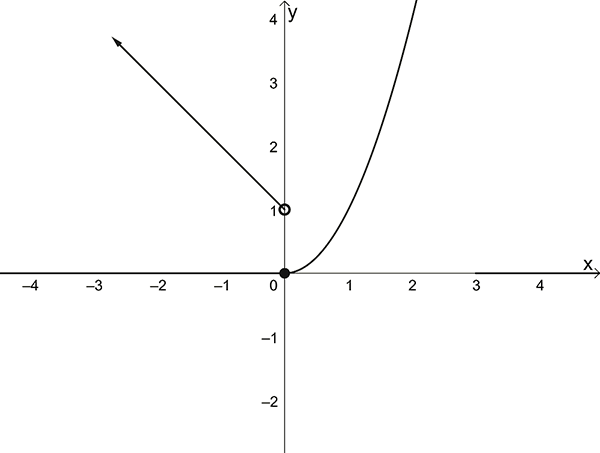
Functions which have different rules for each subset of the domain are called hybrid functions. Sometimes they are referred to as piecewise defined functions.
Introduction
Functions which have different rules for each subset of the domain are called hybrid functions.
Sometimes they are referred to as piece-wise defined functions.
An example of a hybrid function is: \[\begin{align*} y=f(x) & =\begin{cases} -x, & x\leq-1\\ 1, & -1<x<1\\ x, & x\geq1. \end{cases} \end{align*}\] Note that this hybrid function has three rules, each depending on the value of \(x\) in it’s domain. A hybrid function may have two or more rules.
Example 1
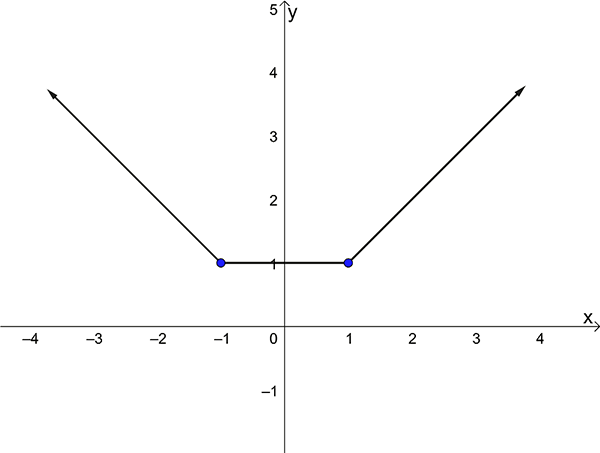
Graph the hybrid function \[\begin{align*} y=f(x) & =\begin{cases} -x, & x\leq-1\\ 1, & -1<x<1\\ x, & x\geq1. \end{cases} \end{align*}\]
Solution:
This is a hybrid function with three rules. We consider the graph of each of the rules, noting the restricted domains:
\(\text{Rule 1. }y=-x\) , \(x\leq-1\)
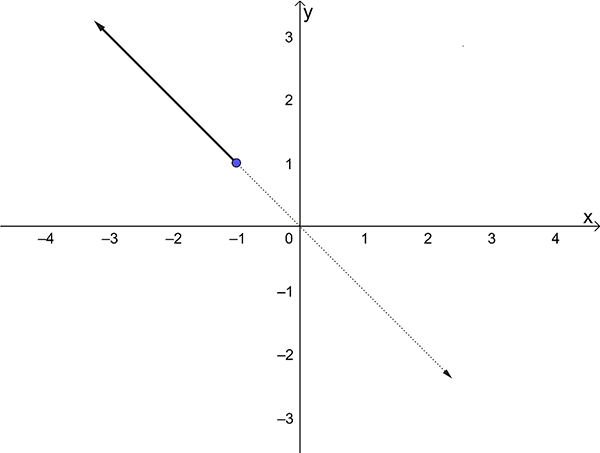
Note that the end point at \(x=-1\) is marked with a filled in circle. This means \(-1\) is in the domain of the function.
Rule 2. \(y=1\) , \(-1<x<1\)
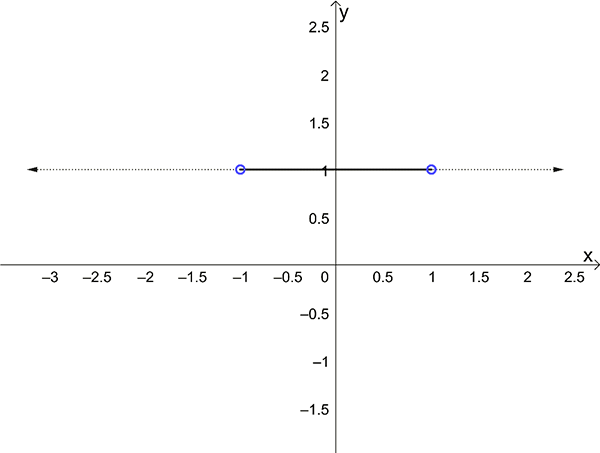
In this case, the open circles indicate that the points \(-1\) and \(1\) are not included in the domain of the function.
Rule 3. \(y=x\) , \(x\geq1\)
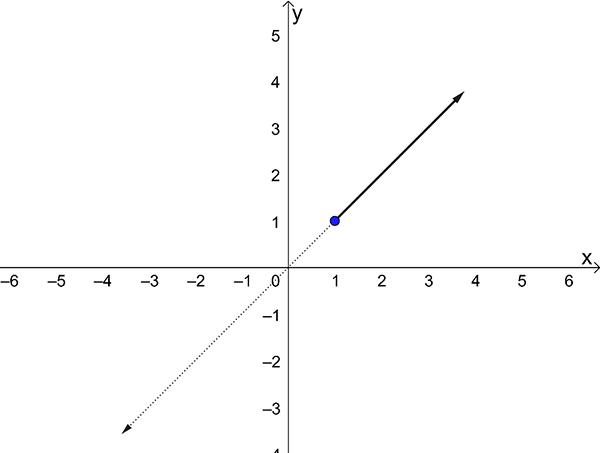
The “graphical pieces” from rules \(1\) to \(3\) above can be put together to form the graph of the hybrid function \[\begin{align*} y=f(x) & =\begin{cases} -x, & x\leq-1\\ 1, & -1<x<1\\ x, & x\geq1 \end{cases} \end{align*}\]
as shown below.
Example 2
Sketch the graph of \[\begin{align*} y & =f\left(x\right)\\ & =\begin{cases} 1-x, & x<0\\ x^{2}, & x\geq0. \end{cases} \end{align*}\]
Solution:
This function has two rules. First rule is \(f\left(x\right)=1-x\) for \(x<0.\) The second rule is \(f\left(x\right)=x^{2}\) for \(x\geq0.\) Graphing each of these and assembling the “graphical pieces” gives the graph for the hybrid function as shown below:
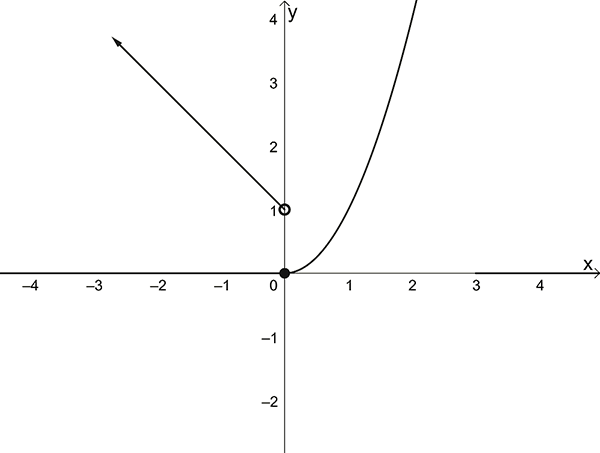
Note the open circle at \(x=0\) as this is not in the domain of the function \(f\left(x\right)=1-x\). However, \(x=0\) is in the domain of \(f\left(x\right)=x^{2}\) and so is shown with a filled dot.
Exercise
\(1.\ \)Draw a sketch graph of \[\begin{align*} f\left(x\right) & =\begin{cases} x+1, & x<0\\ x-1, & x\geq0. \end{cases} \end{align*}\]
\(2.\ \)Draw a sketch graph of \[\begin{align*} f\left(x\right) & =\begin{cases} x^{2}, & x<0\\ -x^{2}, & x\geq0. \end{cases} \end{align*}\]
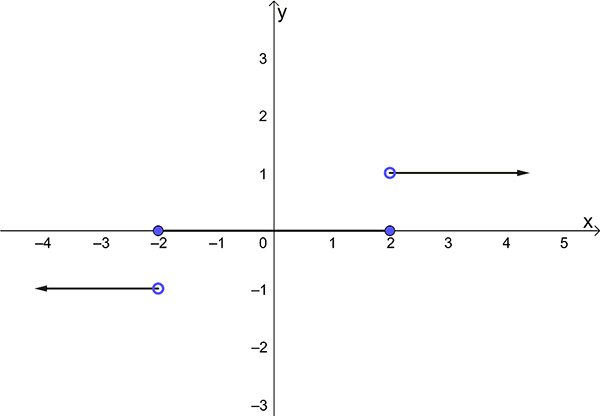
\(3.\ \)Draw a sketch graph of \[\begin{align*} f\left(x\right) & =\begin{cases} -1, & x<-2\\ 0, & -2\leq x\leq2\\ 1, & x>2. \end{cases} \end{align*}\]
\(4.\ \)Draw a sketch graph of \[\begin{align*} f(x) & =\begin{cases} x+2, & x<-1\\ 1, & -1\leq x\leq1\\ x, & x>1. \end{cases} \end{align*}\]
Download this page, FG5 Hybrid Functions (PDF 301 KB)
What's next... FG6 Circular functions