FG3 Inverse notation
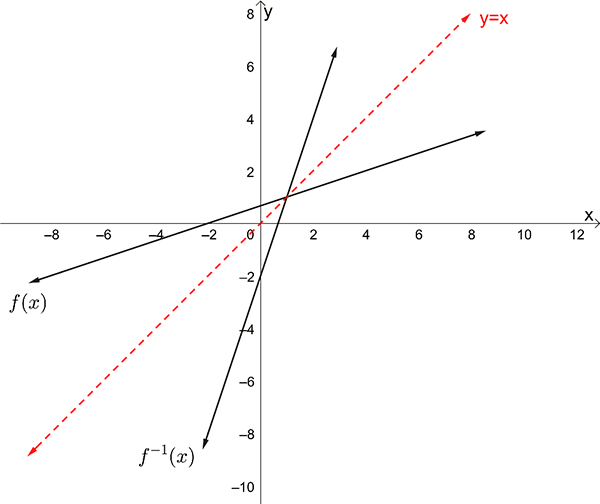
If f-1(x) is the inverse function of a one-to-one function f(x) then f-1(x) is the set of ordered pairs obtained by interchanging the first and second elements in each ordered pair.
Definition of an Inverse Function
If \(f^{-1}(x)\) is the inverse funtion of a one-to-one function \(f(x)\) then \(f^{-1}(x)\) is the set of all ordered pairs obtained by interchanging the first and second elements in each ordered pair.
So if \((a,b)\in f\) then \((b,a)\in f^{-1}\) and if \(f(a)=b\) then \(f^{-1}(b)=a\)
The domain of \(f\) is the range of \(f^{-1}\) and the range of \(f\) is the domain of \(f^{-1}\)
For example the function \(f:R\rightarrow R\), defined by \(y=f(x)=\frac{x-1}{2}\) has an inverse function with the rule \(y=2x+1\) .
So \((3,1)\) belongs to \(f\) and \((1,3)\) belongs to \(f^{-1}\) and \((-7,-4)\) belongs to \(f\) and \((-4,-7)\) belongs to \(f^{-1}\) .
Graph of an Inverse Function
The graphs of any one-to-one function, \(f\) , and its inverse, \(f^{-1}\) , are symmetric about the line \(y=x\) .

Finding an Inverse Function for \(y=f(x)\)
To obtain the rule for an inverse function, swap the \(x\) and \(y\) coordinates in \(f\) and rearrange to express \(y\) in terms of \(x\) .
Example
Find the inverse function of \(f\) where \(f(x)=2-3x\)
\[\begin{align*} y & =2-3x\\ x & =2-3y\text{ $\quad$ (swap the $x\text{ and $y)$ }$ }\\ x-2 & =-3y\text{ $\quad$ (rearrange to make $y$ the subject)}\\ -x+2 & =3y\\ \frac{-x+2}{3} & =y\\ f^{-1}(x) & =\frac{-x+2}{3} \end{align*}\]
Exercise
Find the inverse of each of the following one-to-one functions:
\(y=x+5\)
\(y=4x\)
\(y=\frac{2x+1}{3}\)
\(y=\sqrt{2x-1}\) , \(x\geq\frac{1}{2}\)
\(f^{-1}(x)=x-5\)
\(f^{-1}(x)=\frac{x}{4}\)
\(f^{-1}(x)=\frac{3x-1}{2}\)
\(f^{-1}(x)=\frac{x^{2}+1}{2}\) , \(x\geq0\)
Download this page, FG3 Inverse Notation (PDF 311 KB)
What's next... FG4 Absolute value functions
