V2 Resolution of vectors

Open image

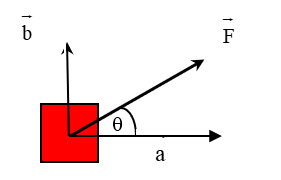
Open imageA Force \(\vec{F}\) at an angle \(\theta\) to the horizontal is broken up horizontally as vector \(\vec{a}\) with magnitude \(\vec{\left|F\right|}cos\theta\) and vertically as vector \(\vec{b}\) with magnitude \(\vec{\left|F\right|}sin\theta\).

Vector quantities in combination will enhance or counteract each other, depending on their direction. An opposing force for example will lessen another force. However, if the forces (or vector quantities) do not act along exactly the same line, it is difficult to know how they will interact.

This task is easier if you can break the vectors into components which are parallel, and then find the result by adding or subtracting parallel components. This technique is very important for resolving forces and other vector quantities in physics.

As with other types of vectors (displacement, velocity, etc.), a force vector can be thought of as being the sum of several other vectors. Imagining that a single force is made up of several forces can greatly simplify calculations, particularly using two imaginary ones at right angles to each other. Usually broken up into vertical and horizontal components. We discuss how to calculate these components in this module.

Components of a Force

If you pull on an object with a force \(\vec{F}\) (see diagram below left), the effect is the same as two other people pulling with forces \(\vec{a}\) and \(\vec{b}\) at right angles to each other , one horizontal and the other vertical (see diagram below right).

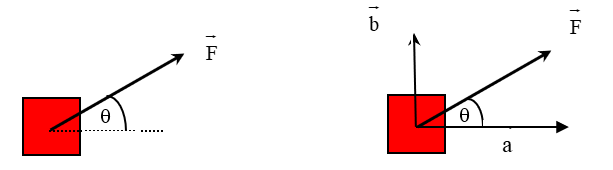
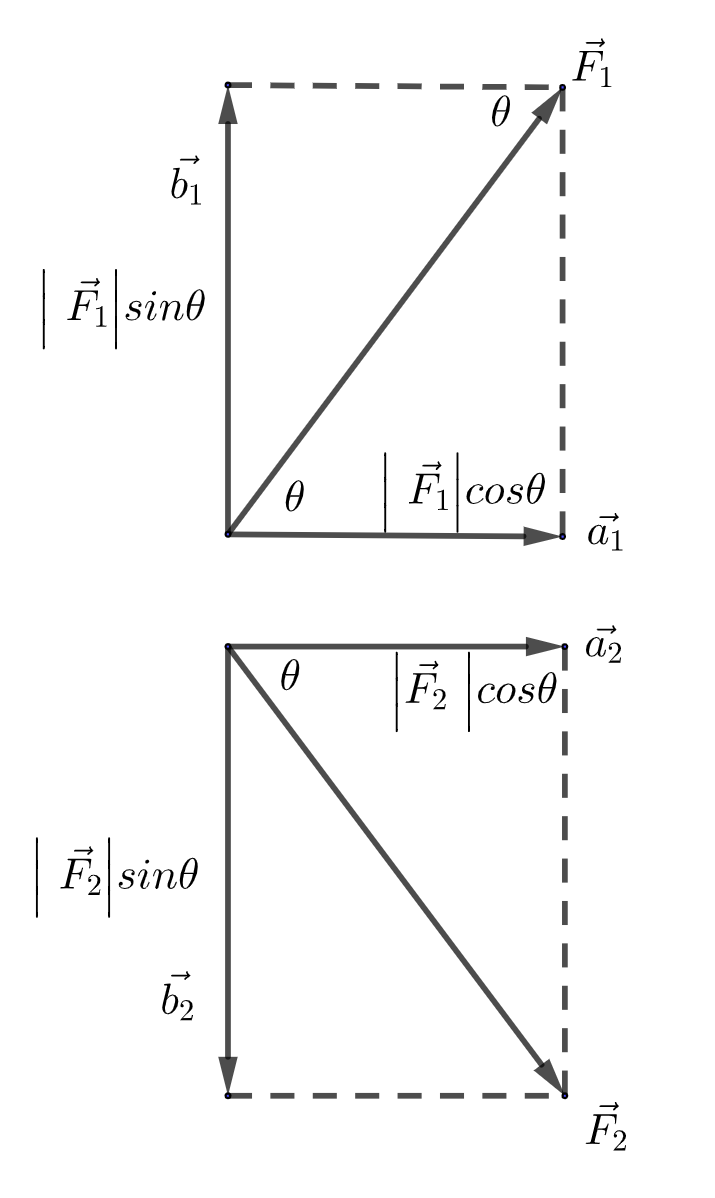
The vector triangle showing the force \(\vec{F}\) and its component vectors \(\vec{a}\) and \(\vec{b}\) is shown.

The force \(\vec{F}\) can be imagined as having two parts, or components, \(\vec{a}\) and \(\vec{b}\) that are at right angles to each other. \(\vec{a}\) is usually called the horizontal component and \(\vec{b}\) the vertical component of \(\vec{F}\). The components are often called rectangular components because they are at right angles to each other.

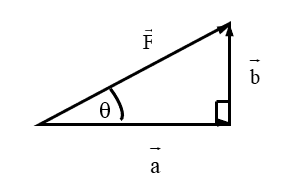
Open image Force vector into two components, a horizontal and b vertical

For the diagram at right it can be seen that the magnitude of the vectors give:

\[\begin{align*} \sin\theta & =\frac{opposite}{hypotenuse}\\ & =\frac{\vec{\left|b\right|}}{\left|\vec{F}\right|}. \end{align*}\]

Transposing gives:

\[\begin{alignat*}{1} \vec{\left|b\right|} & =\vec{\left|F\right|}\sin\theta \end{alignat*}\]

and

\[\begin{alignat*}{1} \cos\theta & =\frac{adjacent}{hypotenuse}\\ & =\frac{\left|\vec{a}\right|}{\left|\vec{F}\right|}. \end{alignat*}\]

Transposing gives:

\[\begin{alignat*}{1} \left|\vec{a}\right| & =\left|\vec{F}\right|\cos\theta \end{alignat*}\]

Example 1

Calculate the rectangular components of a force of 10 Newton that acts in a direction of North 30 degrees East?

Since there is 90 degrees in a right angle triangle we can deduce that the direction of force can be shown as East 60 degrees North.

The force and its rectangular components are shown. One component , \(\vec{a}\), is acting to the East , the other , \(\vec{b}\) , is to the North.

The magnitudes of these forces can be calculated:

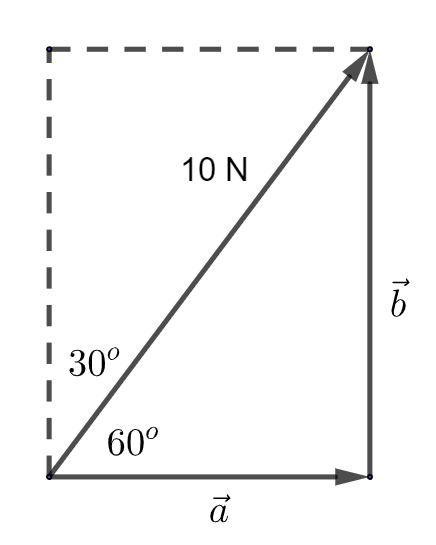
Open image Force of 10 Newtons in terms of horizontal and vertical components

\[\begin{align*} \vec{\left|a\right|} & =\vec{\left|F\right|}\cos\theta\\ & =10\cos60\\ & =5Newton \end{align*}\]

also: \[\begin{alignat*}{1} \vec{\left|b\right|} & =\vec{\left|F\right|}\sin\theta\\ & =10\sin60\\ & =8.7Newton. \end{alignat*}\]

Thus, the 10 Newton force can be resolved into two rectangular components: 5 Newton to the East and 8.7 Newton to the North.

Example 2

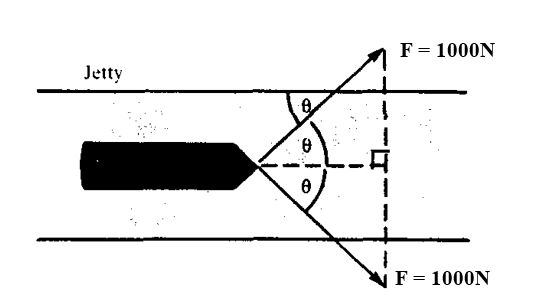
A small boat is being towed at constant speed along a canal by two men walking along the banks on opposite sides pulling with equal forces of \(1000\) Newton at equal angles on ropes attached to the boat. \(\theta=60\) degrees. Calculate the force each man pulls on the rope \((a)\) parallel to the bank, and \((b)\) at right angles to the bank.

The force towards the Jetty an be defined as \(\vec{F_{1}}\) and the force towards the other bank can be defined as \(\vec{F_{2}}\).

Solution:

The 1000 Newton force:

\((a)\) A component force parallel to the bank of

\(\left|\vec{a_{1}}\right|=\left|\vec{F}_{1}\right|\cos\theta=1000\cos60=500\) Newton and

\(\vec{\left|a_{2}\right|}=\left|\vec{F}_{2}\right|\cos\theta=1000\cos60=500\) Newton

\((b)\) A component force at right angles to the bank of

\(\left|\vec{b_{1}}\right|=\left|\vec{F}_{1}\right|\sin\theta=1000\sin60=866\) Newton towards the jetty

\(\left|\vec{b_{2}}\right|=\left|\vec{F}_{2}\right|\sin\theta=1000\sin60=866\) Newton away from the jetty

Open image Resolution of forces on boat

Note that the two components at right angles to the bank are equal in size, but are in opposite directions, so they cancel each other. So the boat will only move parallel to the banks.

Open imageNote: There is zero resultant force at right angles to the Jetty. \(866\) N towards the Jetty and \(866\) N away from the Jetty.

The two components parallel to the banks are in the same direction so the force pulling the boat forwards is:

\(\left|\vec{a_{1}}\right|+\left|\vec{a_{2}}\right|=500+500=2\times F\cos\theta\) \(=2\times500=1000\) Newton.

The balancing force causing the boat to move at constant speed is the friction or drag of the boat through the water acting in the opposite direction.

Exercise:

What is the horizontal component of a force 11 Newton acting at \(\theta=60\) degrees to the horizontal?
Answer: \(5.5\) Newton
What is the northerly component of a wind blowing at \(15ms^{-1}\) from the South East?
Answer: \(11ms^{-1}\)
What is the vector whose components are 3 Newton horizontally and 4 Newton vertically?
Answer: \(5\) Newton \(50\) degrees above the horizontal
What are the vertical and horizontal components of a force of 24 Newton acting at \(\theta=30\) degrees to the horizontal?
Answer: \(12\) Newton vertical and \(22\) Newton horizontal
A plane taking off leaves the runway at \(\theta=32\) degrees to the horizontal traveling at \(180kmh^{-1}.\) How long will it take to climb to an altitude of \(1000\) meter.
Answer: \(37.8\) seconds