V9 Intersecting planes
Two 2-dimensional planes will slice through each other (unless they are parallel). Where they slice will be defined by a straight line. There will also be an angle between the two planes.
Learn how to determine the angle between two intersecting planes and the equation of the line of intersection.
(See also Linear graphs)
Introduction
When two planes in three dimensions intersect, the set of points in the intersection forms a line. However two planes do not form lines if they are parallel and hence never intersect.
This module considers the angle between two planes when they are not parallel.
Definition of a Plane
A plane in three dimensions is a set of points satisfying the equation \[\begin{align*} ax+by+cz & =d \end{align*}\] where \(a,\,b,\,c\) and \(d\) are constants.
Normal to a Plane
The normal \(\vec{N}\), of a plane \[\begin{align*} ax+by+cz & =d \end{align*}\] is a vector at right angles to the plane and has the form \[\begin{align*} \vec{N} & =a\hat{i}+b\hat{j}+c\hat{k}. \end{align*}\] Of course, another normal is given by \(-\vec{N}=-a\hat{i}-b\hat{j}-c\hat{k}\) as this just a vecor in the opposite direction of \(\vec{N}\) and is still at right angles to the plane.
The Angle Between Two Planes
The angle between two intersecting planes is the same as the angle between the normals of the planes.
If \(N_{1}\) and \(N_{2}\)are the normals of two intersecting planes, we know that1 This follows from the definition of the dot or scalar product.
\[\begin{align*} \overrightarrow{N_{1}}.\overrightarrow{N_{2}} & =\left|\overrightarrow{N_{1}}\right|\left|\overrightarrow{N_{2}}\right|\cos\theta \end{align*}\] where \(\theta\) is the angle between them.
Rearranging , we find :
\[\begin{align*} \cos\theta & =\frac{\overrightarrow{N_{1}}.\overrightarrow{N_{2}}}{\left|\overrightarrow{N_{1}}\right|\left|\overrightarrow{N_{2}}\right|}. \end{align*}\] Note that there are in general two possible angles. One is obtuse, the other is acute. Together they sum to \(180^{\circ}.\)
If we wish to find only the acute angle between the planes then we say that:
\[\begin{align*} \cos\theta & =\frac{\left|\overrightarrow{N_{1}}.\overrightarrow{N_{2}}\right|}{\left|\overrightarrow{N_{1}}\right|\left|\overrightarrow{N_{2}}\right|} \end{align*}\]
Example
Find the acute angle of intersection of the planes \(x+y+z=0\) and \(x-3y+z=1\).
The plane \(x+y+z=0\) has the normal vector \(\overrightarrow{N_{1}}=\overrightarrow{i}+\overrightarrow{j}+\overrightarrow{k}\).
The plane \(x-3y+z=1\) has the normal vector \(\overrightarrow{N_{2}}=\overrightarrow{i}-3\overrightarrow{j}+\overrightarrow{k}.\)
Remember:
\[\begin{alignat*}{1} \cos\theta & =\frac{\left|\overrightarrow{N_{1}}.\overrightarrow{N_{2}}\right|}{\left|\overrightarrow{N_{1}}\right|\left|\overrightarrow{N_{2}}\right|} \end{alignat*}\]
so:
\[\begin{alignat*}{1} \left|\overrightarrow{N_{1}}.\overrightarrow{N_{2}}\right| & =\left|\left(1\times1\right)+\left(1\times-3\right)+\left(1\times1\right)\right|\\ & =\left|-1\right|\\ & =1 \end{alignat*}\]
and:
\[\begin{alignat*}{1} \left|\overrightarrow{N_{1}}\right| & =\sqrt{1^{2}+1^{2}+1^{2}}\\ & =\sqrt{3} \end{alignat*}\]
and:
\[\begin{alignat*}{1} \left|\overrightarrow{N_{2}}\right| & =\sqrt{1^{2}+3^{2}+1^{2}}\\ & =\sqrt{11} \end{alignat*}\]
Therefore:
\[\begin{align*} \cos\theta & =\frac{1}{\sqrt{3}\sqrt{11}}\simeq0.1741 \end{align*}\]
Rearranging formula and using inverse \(\cos\) gives:
\[\begin{align*} \theta & =\cos^{-1}\left(0.1741\right)\simeq80^{o} \end{align*}\]
So the angle of intersection of the two planes is approximately \(80\) degrees.
Exercise
Find the angle of intersection of the following planes
The plane \(x-y+z=1\) and \(2x+y-z=3\)
Answer: \(90\) degrees.The plane \(2x+y-z=2\) and \(3x+y-z=3\)
Answer: \(10\) degrees.
Line of Intersection of Two Planes
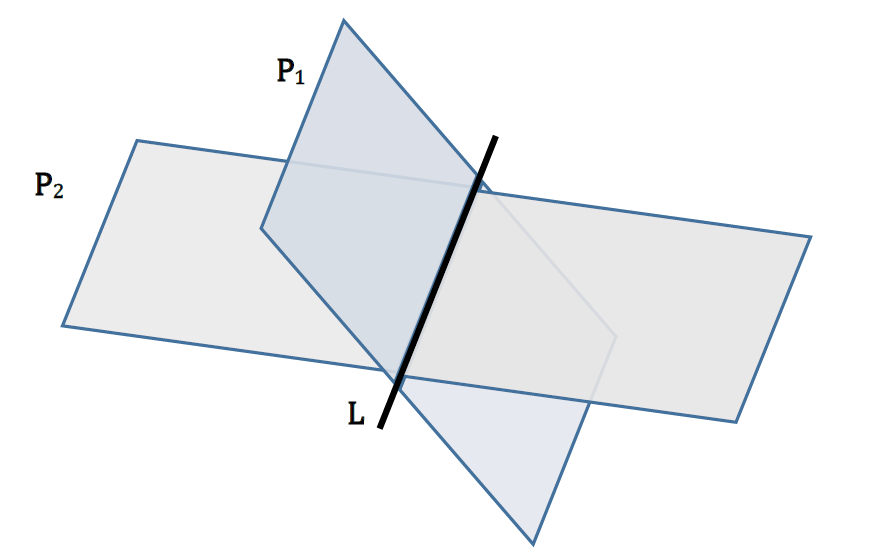
The planes, \(P_{1}\)and \(P_{2}\) intersect along the line L, as in the diagram below:

We want to find the equation of the line of intersection, \(L.\)
Example
If \(P_{1}\): \(2x+4y-z=4\) and \(P_{2}\): \(x-2y+z=3\) , find the parametric equations of the line of intersection of the two planes.
Solution:
Given \(2x+4y-z=4\) and \(x-2y+z=3\), we have two equations but three unknowns. This is a clue to introduce a parameter.2 We will set \(z=t\) but you can set \(x=t\) or \(y=t\). This will generate a set of equations that may look different to what we show below, but they are correct. Let \(z=t\) then the equations of the planes become
\[\begin{alignat*}{2} 2x+4y-t & =4 & \left(1\right)\\ x-2y+t & =3. & \left(2\right) \end{alignat*}\]
Multiplying \(\left(2\right)\) by \(-2\), the equations become:
\[\begin{alignat*}{1} 2x+4y-t & =4\\ -2x+4y-2t & =-6 \end{alignat*}\]
adding these two equations we get:
\[\begin{alignat*}{1} 8y-3t & =-2\\ 8y & =3t-2\\ y & =\frac{3}{8}t-\frac{1}{4}. \end{alignat*}\]
Substituting \(y\) in equation \(\left(2\right)\)
\[\begin{alignat*}{1} x-2\left(\frac{3}{8}t-\frac{1}{4}\right)+t & =3\\ x-\frac{6}{8}t+\frac{2}{4}+t & =3\\ x+\frac{1}{4}t+\frac{1}{2} & =3\\ x & =3-\frac{1}{4}t-\frac{1}{2}\\ x & =\frac{5}{2}-\frac{1}{4}t. \end{alignat*}\]
Hence the parametric equations of the line of the intersection of the two planes are:
\[\begin{alignat*}{1} x=\frac{5}{2}-\frac{1}{4}t,\,y & =\frac{3}{8}t-\frac{1}{4}\text{ and $z=t.$ } \end{alignat*}\]
Exercise
Find the parametric line of intersection and the angle of intersection of the planes \(x+y+2z=0\) and \(2x-y+z=5\).
Answer: Line is \(x=2-t\) ; \(y=-1-t\) ; \(z=t\). Angle is \(60\)degrees.
Download this page: V9 Intersecting Planes (PDF 133KB)
What's next... V10 Distance from a point to a plane
