V5 Projection of vectors

Open image

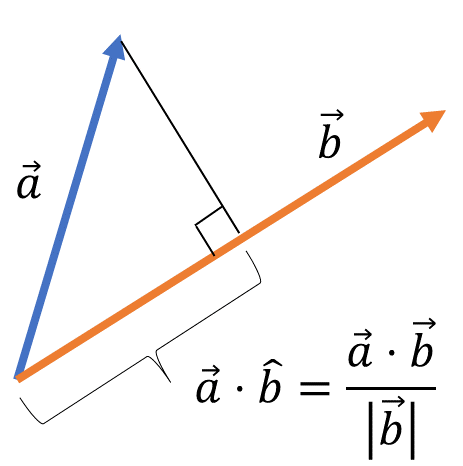
In Resolution of vectors we learned how to resolve vectors in two dimensions along horizontal and vertical axes. It is also possible to resolve one vector along the line of another vector (instead of along the x-y axes).

(See also Linear graphs)

Learn how to find the projection (resolution) of one vector in the direction of a second vector.

There are two types of vector projection:

Scalar projection
Vector projection

For scalar projection, we calculate the length (a scalar quantity) of a vector in a particular direction.

For vector projection we calculate the vector component of a vector in a given direction.

Often, in Physics, Engineering and Mathematics courses you are asked to resolve a vector into two component vectors that are perpendicular to one another. As an example, in the diagram below a vector \(\vec{a}\) is the projection of \(\overrightarrow{F}\) in the horizontal direction while \(\vec{b}\) is the projection of \(\overrightarrow{F}\) in the vertical direction.

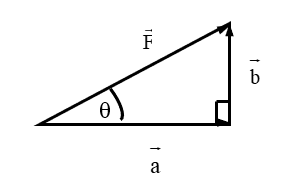
You can project a vector in any direction, not only horizontally and vertically.

This module discusses both scalar and vector projections.

Scalar Projection

Consider the following diagram:

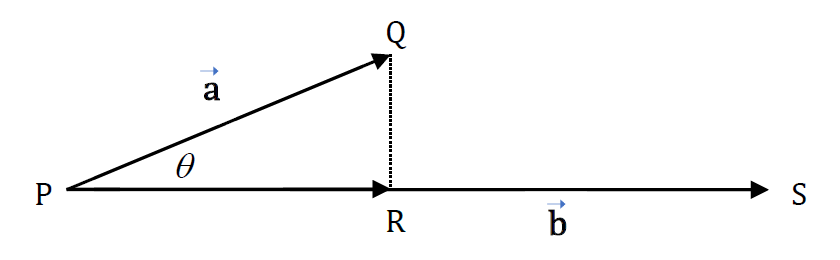
Let \(\overrightarrow{PQ}=\vec{a}\) and \(\overrightarrow{PS}=\vec{b}.\) The scalar projection of the vector \(\vec{a}\) in the direction of vector \(\vec{b}\) is the length of the straight line \(PR\) or \(\left|\overrightarrow{PR}\right|\)where 11 Remember that the magnitude (or length) of a vector \(\vec{v}=v_{1}\vec{i}+v_{2}\vec{j}+v_{3}\vec{k}\) is denoted by \[\begin{align*} \left|\vec{v}\right| & =\sqrt{v_{1}^{2}+v_{2}^{2}+v_{3}^{2}} \end{align*}\] For example, if \(\vec{v}=2\vec{i}-3\vec{j}+\vec{k}\) then \[\begin{align*} \left|\vec{v}\right| & =\sqrt{2^{2}+\left(-3\right)^{2}+1^{2}}\\ & =\sqrt{4+9+1}\\ & =\sqrt{14} \end{align*}\]

\[\begin{align*} \cos\left(\theta\right) & =\frac{\text{adjacent}}{\text{hypotenuse}}\\ & =\frac{\left|\overrightarrow{PR}\right|}{\left|\vec{a}\right|}. \end{align*}\] Rearranging gives, \[\begin{align*} \left|\overrightarrow{PR}\right| & =\left|\vec{a}\right|\cos\left(\theta\right). & \left(1\right) \end{align*}\] This may be written in terms of the dot product.22 The dot product (or scalar product) of two vectors \[\begin{align*} \vec{a} & =a_{1}\vec{i}+a_{2}\vec{j}+a_{3}\vec{k}\\ \vec{b} & =b_{1}\vec{i}+b_{2}\vec{j}+b_{3}\vec{k} \end{align*}\] is defined to be \[\begin{align*} \vec{a}\cdot\vec{b} & =\left|\vec{a}\right|\left|\vec{b}\right|\cos\left(\theta\right) \end{align*}\] An alternate definition is \[\begin{align*} \vec{a}\cdot\vec{b} & =a_{1}b_{1}+a_{2}b_{2}+a_{3}b_{3}. \end{align*}\]

We know \[\begin{align*} \vec{a}\cdot\vec{b} & =\left|\vec{a}\right|\left|\vec{b}\right|\cos\left(\theta\right) \end{align*}\] and so \[\begin{align*} \cos\left(\theta\right) & =\frac{\vec{a}\cdot\vec{b}}{\left|\vec{a}\right|\left|\vec{b}\right|}. \end{align*}\]

Substituting this expression for \(\cos\left(\theta\right)\) into eqn\(\left(1\right)\) above gives:

\[\begin{align*} \left|\overrightarrow{PR}\right| & =\left|\vec{a}\right|\cos\left(\theta\right)\\ \left|\overrightarrow{PR}\right| & =\left|\vec{a}\right|\frac{\vec{a}\cdot\vec{b}}{\left|\vec{a}\right|\cdot\left|\vec{b}\right|}\\ & =\frac{\vec{a}\cdot b}{\left|\vec{b}\right|}\\ & =\vec{a}\cdot\frac{\vec{b}}{\left|\vec{b}\right|}\\ & =\vec{a}\cdot\hat{b} \end{align*}\]

where \(\hat{b}=\frac{\vec{b}}{\left|\vec{b}\right|}\) is the unit vector in the direction of \(\vec{b}\).33 A unit vector for the vector \(\vec{b}\) is denoted by \(\hat{b}\) and is the vector \(\vec{b}\) divided by its length \(\left|\vec{b}\right|\). That is \[\begin{align*} \hat{b} & =\frac{\vec{b}}{\left|\vec{b}\right|}. \end{align*}\] A unit vector is a vector of length one in the direction of the original vector.

The scalar projection of a vector \(\vec{a}\) in the direction of vector \(\vec{b}\) is given by:

\[\begin{alignat*}{1} \frac{\vec{a}\cdot\vec{b}}{\left|\vec{b}\right|} & =\vec{a}\cdot\hat{b}\\ & =\left|\vec{a}\right|\cos\theta \end{alignat*}\]

Example

Find the scalar projection of the vector \(\vec{a}=(2,3,1)\) in the direction of vector \(\vec{b}=(5,-2,2)\).

Solution:
The magnitude of \(\vec{b}\) is

\[\begin{alignat*}{1} \left|\vec{b}\right| & =\sqrt{5^{2}+(-2)^{2}+2^{2}}\\ & =\sqrt{25+4+4}\\ & =\sqrt{33} \end{alignat*}\]

therefore \[\begin{alignat*}{1} \hat{b} & =\frac{\vec{b}}{\left|\vec{b}\right|}\\ & =\frac{(5,-2,2)}{\sqrt{33}}\\ & =\frac{1}{\sqrt{33}}(5,-2,2) \end{alignat*}\]

so the scalar projection of \(\vec{a}\) in the direction of \(\vec{b}\) is:

\[\begin{alignat*}{1} \vec{a}\cdot\hat{b} & =(2,3,1)\cdot\frac{(5,-2,2)}{\sqrt{33}}\\ & =\frac{\left(2\times5\right)+\left(3\times\left(-2\right)\right)+\left(1\times2\right)}{\sqrt{33}}\\ & =\frac{10-6+2}{\sqrt{33}}\\ & =\frac{6}{\sqrt{33}}. \end{alignat*}\]

Vector Projection

The vector projection of a vector \(\vec{a}\) in the direction of vector \(\vec{b}\) is a vector in the direction of \(\vec{b}\) with magnitude equal to the length of the straight line \(PR\) or \(\left|\overrightarrow{PR}\right|\) as shown below.

Therefore the vector projection of \(\vec{a}\) in the direction of \(\vec{b}\) is the scalar projection multiplied by a unit vector in the direction of \(\vec{b}\).

The vector projection of vector \(\vec{a}\) in the direction of vector \(\vec{b}\) is:

\[\begin{alignat*}{1} \left(\vec{a}\cdot\hat{b}\right)\hat{b} & =\frac{\left(\vec{a}\cdot\vec{b}\right)\vec{b}}{\left|\vec{b}\right|^{2}} \end{alignat*}\]

Example 1

Find the vector projection of vector \(\vec{a}=(2,3,1)\) in the direction of vector \(\vec{b}=(5,-2,2)\).

Solution:

The vector projection \(\vec{a}\) in the direction of \(\vec{b}\) equals:44 Remember that \[\begin{align*} \left|\vec{b}\right| & =\sqrt{5^{2}+(-2)^{2}+2^{2}}\\ & =\sqrt{33} \end{align*}\]

\[\begin{alignat*}{1} \left(\vec{a}\cdot\hat{b}\right)\hat{b} & =\frac{\left(\vec{a\cdot}\vec{b}\right)\vec{b}}{\left|\vec{b}\right|^{2}}\\ & =\frac{\left(\left(2,3,1\right)\cdot\left(5,-2,2\right)\right)\left(5,-2,2\right)}{\left(\sqrt{33}\right)^{2}}\\ & =\frac{\left(2\times5+3\times\left(-2\right)+1\times2\right)\left(5,-2,2\right)}{33}\\ & =\frac{\left(10-6+2\right)\left(5,-2,2\right)}{33}\\ & =\frac{\left(6\right)\left(5,-2,2\right)}{33} \end{alignat*}\]

The vector projection of \(\vec{a}\) in the direction of \(\vec{b}\) is

\[\begin{alignat*}{1} \frac{6\left(5,-2,2\right)}{33} & =\frac{6}{33}\left(5,-2,2\right)\\ & =\frac{2}{11}\left(5\hat{i}-2\hat{j}+2\hat{k}\right). \end{alignat*}\]

Example 2

If \(\vec{a}=(1,-2,2)\) and \(\vec{b}=(5,-2,2)\) find:

\((a)\) The scalar projection of \(\vec{a}\) in the direction of \(\vec{b}\).

\((b)\) The vector projection of \(\vec{a}\) in the direction of \(\vec{b}\).

Solution:

\((a)\) The scalar projection of \(\vec{a}\) in the direction of \(\vec{b}\) is \(\vec{a}\cdot\hat{b}\).

If \[\begin{alignat*}{1} \vec{b} & =(5,-2,2) \end{alignat*}\]

then \[\begin{alignat*}{1} \left|\vec{b}\right| & =\sqrt{33} \end{alignat*}\]

and \[\begin{alignat*}{1} \hat{b} & =\frac{\vec{b}}{\left|\vec{b}\right|}\\ & =\frac{\left(5,-2,2\right)}{\sqrt{33}}\\ & =\frac{1}{\sqrt{33}}\left(5,-2,2\right). \end{alignat*}\]

Therefore \[\begin{alignat*}{1} \vec{a}\cdot\hat{b} & =\left(1,-2,2\right)\cdot\frac{\left(5,-2,2\right)}{\sqrt{33}}\\ & =\frac{\left(\left(1\times5\right)+\left(\left(-2\right)\times\left(-2\right)\right)+\left(2\times2\right)\right)}{\sqrt{33}}\\ & =\frac{\left(5+4+4\right)}{\sqrt{33}}\\ & =\frac{13}{\sqrt{33}}. \end{alignat*}\] The scalar projection is \(13/\sqrt{33}.\)

\((b)\) The vector projection of \(\vec{a}\) in the direction of \(\vec{b}\) is \(\left(\vec{a}\cdot\hat{b}\right)\hat{b}\)

from part \((a)\) \[\begin{alignat*}{1} \vec{a}\cdot\hat{b} & =\frac{13}{\sqrt{33}} \end{alignat*}\]

so that the vector projection of \(\vec{a}\) in the direction of \(\vec{b}\) is \[\begin{alignat*}{1} \left(\vec{a}\cdot\hat{b}\right)\hat{b} & =\left(\frac{13}{\sqrt{33}}\right)\frac{(5,-2,2)}{\sqrt{33}}\\ & =\frac{13(5,-2,2)}{33}\\ & =\frac{13}{33}(5,-2,2)\\ & =\frac{13}{33}\left(5\hat{i}-2\hat{j}+2\hat{k}\right) \end{alignat*}\] The vector projection is \(\frac{13}{33}(5,-2,2)\) or \(\frac{13}{33}\left(5\hat{i}-2\hat{j}+2\hat{k}\right)\)

Exercise 1

For \(\vec{a}=\left(2,3,1\right)\) , \(\vec{b}=\left(5,0,3\right)\) , \(\vec{c}=\left(0,0,3\right)\) and \(\vec{d}=\left(-2,2,-1\right)\) find:

The scalar projection of \(\vec{a}\) in the direction of \(\vec{b}\).
Answer: \(\frac{13}{34}\)
The vector projection of \(\vec{a}\) in the direction of \(\vec{b}\).
Answer: \(\frac{13}{34}\left(5,0,3\right)\)
The scalar projection of \(\vec{c}\) in the direction of \(\vec{b}\).
Answer: \(\frac{9}{\sqrt{34}}\)
The vector projection of \(\vec{c}\) in the direction of \(\vec{a}\).
Answer: \(\frac{3}{14}\left(2,3,1\right)\)
The vector projection of \(\vec{d}\) in the direction of \(\vec{a}\).
Answer: \(\frac{1}{14}\left(2,3,1\right)\)
The vector projection of \(\vec{b}\) in the direction of \(\vec{d}\).
Answer: \(\frac{-13}{9}\left(-2,2,-1\right)\)

Exercise 2

For \(\vec{a}=\left(2,0,-1\right)\) , \(\vec{b}=\left(3,5,6\right)\) find:

Find the scalar projection of \(\vec{a}\) in the direction of \(\vec{b}\).
Answer: 0
What can you say about the relationship between \(\vec{a}\) and \(\vec{b}\)?
Answer: \(\vec{a}\) and \(\vec{b}\) are perpendicular. Remember \(\cos90^{\circ}=0\) and see equation (1) above.