IN8 Integration by parts
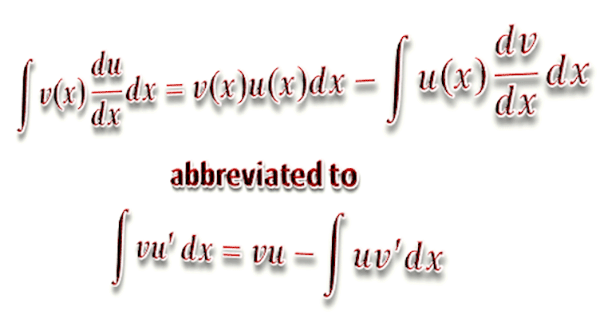
If you can consider your expression to be a product (i.e. Multiplication x) of two functions, you can integrate this using Integration by parts. This reflects the product rule in differentiation and is applicable to logarithmic, exponential, trigonometric and algebraic functions.
Integration by parts is a technique for integrating the product of two functions. For example: \[ \int x\cos\left(x\right)dx \] where the functions are \(x\) and \(\cos\left(x\right)\) or \[ \int x^{3}\ln\left(x\right)dx \] where the functions are \(x^{3}\) and \(\ln\left(x\right)\). This module gives some information on using this technique.
Formula
The integration by parts formula is obtained from the product rule for differentiation. For any two differentiable functions \(v\left(x\right)\) and \(u\left(x\right)\) we have, by the product rule, \[\begin{align*} \frac{d}{dx}\left(v\left(x\right)u\left(x\right)\right) & =v\left(x\right)\frac{du\left(x\right)}{dx}+u\left(x\right)\frac{dv\left(x\right)}{dx}. \end{align*}\] Integrating both sides with respect to \(x\) gives \[\begin{align*} \int\frac{d}{dx}\left(v\left(x\right)u\left(x\right)\right)dx & =\int\left(v\left(x\right)\frac{du\left(x\right)}{dx}+u\left(x\right)\frac{dv\left(x\right)}{dx}\right)dx,\;\textrm{that is,}\\ v\left(x\right)u\left(x\right) & =\int v\left(x\right)\frac{du\left(x\right)}{dx}dx+\int u\left(x\right)\frac{dv\left(x\right)}{dx}dx. \end{align*}\] This can be rearranged to give the formula for integration by parts: \[\begin{align*} \int v\left(x\right)\frac{du\left(x\right)}{dx}dx & =v\left(x\right)u\left(x\right)-\int u\left(x\right)\frac{dv\left(x\right)}{dx}dx. \end{align*}\] Which is often abbreviated to \[\begin{align*} \int vu'dx & =vu-\int uv'dx. \end{align*}\]
The hope is that by choosing the functions \(v\) and \(u'\) carefully, the integral on the right hand side is easier than the original integral. Successful use of integration by parts requires a correct choice for \(v\) and \(u'\). If the integral on the right is harder, then try swapping \(v\) and \(u'\).
To assist you in choosing \(v\) and \(u'\) choose \(v\) to be the function that comes first in the sequence of functions:
logarithmic function
inverse trig function
algebraic function
trigonometric function
exponential function
\(u'\) is then the other function in the integrand. 1 The integrand is the function that is being integrated. For example the integrand in \[ \int x\sin\left(x\right)dx \] is \(x\sin\left(x\right)\). In this case it is the product of an algebraic function \(x\) and a trigonometric function \(\sin\left(x\right)\) so we would set \(v=x\), (because algebraic functions are higher on the list than trigonometric functions), and \(u'=\sin\left(x\right)\).
Example 1: Find \(\int x\cos\left(x\right)dx\).
Here we have an algebraic function \(x\) and a trigonometric function \(\cos\left(x\right)\). Since algebraic functions are higher on the list than trigonometric functions, we let \(v=x\) and so \(u'=du/dx=\cos\left(x\right)\). Then \(v'=dv/dx=1\) and \(u=\sin\left(x\right)\). Using the formula we have: 2 We use \[\begin{align*} \int vu'dx & =vu-\int uv'dx. \end{align*}\] and the fact that \(\sin\left(x\right)=\sin\left(x\right)\times1\). \[\begin{align*} \int x\cos\left(x\right)dx & =vu-\int uv'dx\\ & =x\sin\left(x\right)-\int\left(\sin\left(x\right)\right)\cdot1dx\\ & =x\sin\left(x\right)+\cos\left(x\right)+c,\;c\textrm{ a constant.} \end{align*}\] Note that if we chose the functions as \(v=\cos\left(x\right)\) and \(u'=x\), then \(v'=-\sin\left(x\right)\) and \(u=\frac{1}{2}x^{2}.\) Substituting in the formula will give: \[\begin{align*} \int x\cos\left(x\right)dx & =vu-\int uv'dx\\ & =-\frac{1}{2}x^{2}\sin\left(x\right)-\int-\frac{1}{2}x^{2}\sin\left(x\right)dx. \end{align*}\] The integral on the right is harder than the one we began with and we make no progress. If this happens to you, change the selection.
Example 2: Find \(\int x^{3}\ln\left(x\right)dx\).
Here we have an algebraic function \(x^{3}\) and a logarithmic function \(\ln\left(x\right)\). Since logarithmic functions are higher on the list than algebraic functions, we let \(v=\ln\left(x\right)\) and so \(u'=du/dx=x^{3}\). Then \(v'=dv/dx=1/x\) and \(u=\frac{1}{4}x^{4}\). Using the formula we have 3 We use \[\begin{align*} \int vu'dx & =vu-\int uv'dx. \end{align*}\] \[\begin{align*} \int x^{3}\ln\left(x\right)dx & =vu-\int uv'dx\\ & =\ln\left(x\right)\left(\frac{1}{4}x^{4}\right)-\int\frac{1}{4}x^{4}\left(\frac{1}{x}\right)dx\\ & =\frac{1}{4}x^{4}\ln\left(x\right)-\frac{1}{4}\int x^{3}dx\\ & =\frac{1}{4}x^{4}\ln\left(x\right)-\frac{1}{4}\frac{1}{4}x^{4}+c\;c\textrm{ a constant}\\ & =\frac{x^{4}\ln\left(x\right)}{4}-\frac{x^{4}}{16}+c. \end{align*}\]
Example 3: Find \(\int\sin^{-1}\left(x\right)dx.\)
We apparently have only one function \(\sin^{-1}\left(x\right)\). The trick here is to note that the integrand 4 The integrand is the function that is integrated. In this case it is \(\sin^{-1}\left(x\right)\) which is the same as \(\sin^{-1}\left(x\right)\times1\). can always be multiplied by \(1\) without change. So instead of seeing \(\int\sin^{-1}\left(x\right)dx.\) We see \(\int\sin^{-1}\left(x\right)\times1dx.\) We can view \(1\) as the constant value function.5 The constant value function \(1\) is just a function that gives the value \(1\) regardless of its argument. That is \(1\left(x\right)=1\) for all \(x\in\mathbb{R}.\) The constant value function is algebraic, \(\left(1=x^{0}\right)\) and below an inverse trigonometric function like \(\sin^{-1}\left(x\right)\) on the list above. So we set \(v=\sin^{-1}\left(x\right)\) and \(du/dx=1,\) then \(dv/dx=1/\sqrt{1-x^{2}}\) and \(u=x.\) Substituting in the formula we get:6 We use \[\begin{align*} \int vu'dx & =vu-\int uv'dx. \end{align*}\] \[\begin{align*} \int\sin^{-1}\left(x\right)dx & =vu-\int uv'dx\\ & =x\sin^{-1}\left(x\right)-\int\frac{x}{\sqrt{1-x^{2}}}dx. & (1) \end{align*}\] The integral on the right hand side can be evaluated with the substitution \(w=1-x^{2}\) then \(dw/dx=-2x\) and \(x=-\frac{1}{2}\frac{dw}{dx}\), using the substitution rule7 The substitution rule states \[ \int f\left(g\left(x\right)\right)\frac{dg}{dx}dx=\int f\left(w\right)dw \] where \(w=g\left(x\right)\). we get \[\begin{align*} \int\frac{x}{\sqrt{1-x^{2}}}dx & =\int-\frac{1}{2}\frac{dw}{dx}\frac{1}{\sqrt{w}}dx\\ & =-\frac{1}{2}\int w^{-1/2}dw\\ & =-\frac{1}{2}\left(2\right)w^{1/2}+c,\;c\in\mathbb{R}\\ & =-\left(1-x^{2}\right)^{1/2}+c\\ & =-\sqrt{1-x^{2}}+c. \end{align*}\] Substituting this result in equation (1) we get the final result \[\begin{align*} \int\sin^{-1}\left(x\right)dx & =vu-\int uv'dx\\ & =x\sin^{-1}\left(x\right)-\int\frac{x}{\sqrt{1-x^{2}}}dx.\\ & =x\sin^{-1}\left(x\right)+\sqrt{1-x^{2}}+c. \end{align*}\]
Repeated Use of Integration by Parts
Some integrals require the use of the integration by parts technique more than once. For example, consider \(\int x^{2}e^{x}dx\). We have an algebraic function \(x^{2}\) multiplying an exponential function \(e^{x}.\) According to our guide we set \(v\left(x\right)=x^{2}\) and \(u'\left(x\right)=e^{x}.\) Then \(dv/dx=2x\) and \(u\left(x\right)=e^{x}.\) Substituting in the integration by parts formula we get: 8 We use \[\begin{align*} \int vu'dx & =vu-\int uv'dx. \end{align*}\] \[\begin{align*} \int x^{2}e^{x}dx & =x^{2}e^{x}-\int e^{x}\left(2x\right)dx. & (2) \end{align*}\] The integral on the right hand side requires another integration by parts. We set \(v\left(x\right)=2x\) and \(u'\left(x\right)=e^{x}.\) Then \(dv/dx=2\) and \(u\left(x\right)=e^{x}.\) Substituting in the integration by parts formula gives \[\begin{align*} \int e^{x}\left(2x\right)dx & =2xe^{x}-\int2e^{x}dx\\ & =2xe^{x}-2e^{x}+c,\;c\in\mathbb{R}. & (3) \end{align*}\] Now substitute this result in equation (2) to get the result \[\begin{align*} \int x^{2}e^{x}dx & =x^{2}e^{x}-\int e^{x}\left(2x\right)dx\\ & =x^{2}e^{x}-\left(2xe^{x}-2e^{x}+c\right)\;\textrm{using ($3$ )}\\ & =x^{2}e^{x}-2xe^{x}+2e^{x}-c\\ & =e^{x}\left(x^{2}-2x+2\right)-c. \end{align*}\] Note that it doesn’t matter if we put \(c\) or \(-c\) as \(c\) is just any constant.
Exercises
\[\begin{array}{lll} \textrm{1. Find}\\ a)\;\int x\sin\left(x\right)dx & & b)\;\int xe^{x}dx\\ c)\;\int x\cos\left(4x\right)dx & & d)\;\int x^{4}\ln\left(x\right)dx\\ \\ \textrm{2. Find}\\ a)\;\int x^{2}\cos\left(x\right)dx & & b)\;\int x^{3}e^{x^{2}}\;\textrm{(Hint: let $v=x^{2})$ } \end{array}\]
\[\begin{array}{llll} 1. & a)\;-x\cos\left(x\right)+\sin\left(x\right)+c & & b)\;xe^{x}-e^{x}+c\\ & c)\;\frac{1}{4}x\sin\left(4x\right)+\frac{1}{16}\cos\left(4x\right)+c & & d)\;\frac{x^{5}}{5}\ln\left(x\right)-\frac{x^{5}}{25}+c\\ \\ 2. & a)\;x^{2}\sin\left(x\right)+2x\cos\left(x\right)-2\sin\left(x\right)+c\\ & b)\;x^{2}e^{x^{2}}-e^{x^{2}}+c \end{array}\]
Download this page, IN8 Integration by Parts (PDF 212 KB)
What's next... IN9 Double integrals
