Skip to content
RMIT University Library - Learning Lab

IN6 Integration by substitution

 
August 11, 2022 - 3:39pm — AJ (e67821)

The rule for integration by substitution

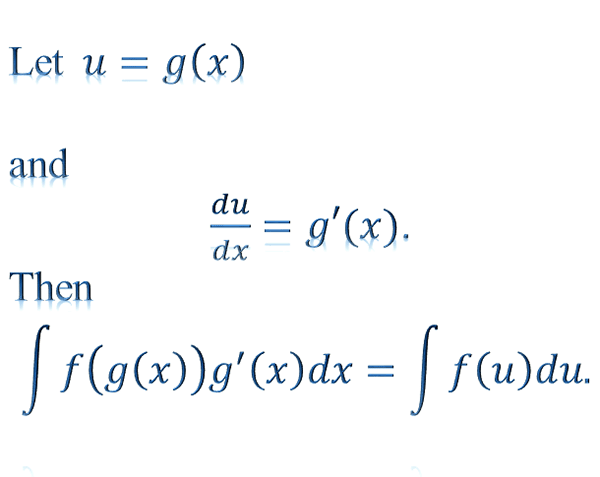
An expression that is composed of two functions (say an algebraic expression nested within a trigonometric expression) can be complicated to integrate. You can simplify this by substituting a single pronumeral (say u) to represent one of the functions. The substitution rule for integration is like the chain rule for differentiation: it breaks a complex expression into manageable parts.

Under some circumstances, it is possible to use the substitution method to carry out an integration. The idea is to make a substitution that makes the original integral easier. Generally, if some part of the integrand is a derivative of another part multiplied by a constant, substitution may be useful. 1 The integrand of an integral is the function being integrated. For example the integrand of the integral \[ \int2x\cos\left(x^{2}\right)dx \] is \(2x\cos x^{2}\).

Integration by Substitution

The basic rule is:

If \(u=g\left(x\right)\) and \(\frac{du}{dx}=g'\left(x\right)\) then \[ \int f\left(g\left(x\right)\right)g'\left(x\right)dx=\int f\left(u\right)du. \]

This may also be written: \[\begin{align*} \int f\left(u\right)\frac{du}{dx}dx & =\int f\left(u\right)du. \end{align*}\]

A simple test may be used to see if substitution is useful. Look at the integrand2 The integrand of an integral is the function being integrated. For example the integrand of the integral \[ \int2x\cos\left(x^{2}\right)dx \] is \(2x\cos x^{2}\). and see if one part of it is the derivative of another part multiplied by a constant. If so, substitution may be helpful. For example consider \[ \int2x\cos\left(x^{2}\right)dx. \] Note that the derivative of \(x^{2}\) is \(2x\) and so one part is the derivative of another part and substitution can be used. Even if we have the integral \[ \int x\cos\left(x^{2}\right)dx \] the derivative of \(x^{2}\) is \(2x\). Since \(x\) is 1/2 of the derivative of \(x^{2}\), substitution is still possible.

Example 1: Calculate \(\int2x\cos\left(x^{2}\right)dx.\)

Solution: In this solution we use the second form of the substitution rule.3 \[ \int f\left(u\right)\frac{du}{dx}dx=\int f\left(u\right)du. \]

Let \(u=x^{2}\) then \(\cos\left(x^{2}\right)=\cos\left(u\right)=f\left(u\right)\) and \(du/dx=2x\). Substituting these in the integral gives \[\begin{align*} \int2x\cos\left(x^{2}\right)dx & =\int\frac{du}{dx}\cos\left(u\right)dx\\ & =\int f\left(u\right)\frac{du}{dx}dx\\ & =\int f\left(u\right)du\quad\textrm{using the substitution rule}\\ & =\int\cos\left(u\right)du\\ & =\sin\left(u\right)+c+c,\;c\textrm{ a constant}\\ & =\sin\left(x^{2}\right)+c. \end{align*}\]

Note that our choice of \(u=x^{2}\) was based on the fact that the derivative is \(2x\) which is part of the integrand.

Example 2: Calculate \(\int x\cos\left(x^{2}\right)dx.\)

Solution: Again set \(u=x^{2}\) because \(du/dx=2x\) and so \(x=\frac{1}{2}\frac{du}{dx}\). As in the first example, \(\cos\left(x^{2}\right)=\cos\left(u\right)=f\left(u\right)\) and substituting in the integral we get \[\begin{align*} \int x\cos\left(x^{2}\right)dx & =\int\frac{1}{2}\frac{du}{dx}\cos\left(u\right)dx\\ & =\frac{1}{2}\int f\left(u\right)\frac{du}{dx}dx\\ & =\frac{1}{2}\int f\left(u\right)du\quad\textrm{using the substitution rule}\\ & =\frac{1}{2}\int\cos\left(u\right)du\\ & =\frac{1}{2}\sin\left(u\right)+c,\;c\textrm{ a constant}\\ & =\frac{1}{2}\sin\left(x^{2}\right)+c \end{align*}\]

Example 3: Find \(\int\left(8x-5\right)^{9}dx\).

Solution: We set \(u=8x-9\) then \(du/dx=8\) so 1=\(\frac{1}{8}du/dx\) and \(\left(8x-5\right)^{9}=u^{9}=f\left(u\right)\). Substituting in the integral we get4 Note that \(\left(8x-5\right)^{9}=1\times\left(8x-5\right)^{9}\). \[\begin{align*} \int\left(8x-5\right)^{9}dx & =\int\frac{1}{8}\frac{du}{dx}u^{9}dx\\ & =\int\frac{1}{8}\frac{du}{dx}f\left(u\right)dx\\ & =\frac{1}{8}\int f\left(u\right)du\quad\textrm{using the substitution rule}\\ & =\frac{1}{8}\int u^{9}du\\ & =\frac{1}{8}\frac{1}{10}u^{10}+c,\;c\textrm{ a constant}\\ & =\frac{1}{80}\left(8x-5\right)^{10}+c. \end{align*}\]

Example 4: Find \(\int x\left(x^{2}+2\right)^{3}dx.\)

Solution: We set \(u=x^{2}+2\) because the derivative \(du/dx=2x\) and \(x=\frac{1}{2}\frac{du}{dx}\). Then \(\left(x^{2}+2\right)^{3}=u^{3}=f\left(u\right)\) and the integral becomes \[\begin{align*} \int x\left(x^{2}+2\right)dx & =\int\frac{1}{2}\frac{du}{dx}u^{3}dx\\ & =\frac{1}{2}\int u^{3}\frac{du}{dx}dx\\ & =\frac{1}{2}\int u^{3}du\\ & =\frac{1}{2}\frac{1}{4}u^{4}+c,\;c\textrm{ a constant}\\ & =\frac{1}{8}\left(x^{2}+4\right)^{4}+c. \end{align*}\] Note in this example we did not put in the steps involving \(f\left(u\right)\) as done previously. These steps are not required and were put in to clarify the use of the substitution rule.

Example 5: Find \(\int x^{2}e^{4-x^{3}}dx.\)

Solution: We set \(u=4-x^{3}\) because \(du/dx=-3x^{2}\) which is \(-3\) times the other part of the integrand. So \(x^{2}=-\frac{1}{3}du/dx.\)Substituting, the integral is:

\[\begin{align*} \int x^{2}e^{4-x^{3}}dx & =\int\left(-\frac{1}{3}\right)\frac{du}{dx}e^{u}dx\\ & =-\frac{1}{3}\int e^{u}\frac{du}{dx}dx\\ & =-\frac{1}{3}\int e^{u}du\\ & =-\frac{1}{3}e^{u}+c,\;c\textrm{ a constant}\\ & =-\frac{1}{3}e^{4-x^{3}}+c. \end{align*}\]

Example 6: Find \(\int\frac{x^{4}}{1+x^{5}}dx.\)

Solution: Let \(u=1+x^{5}\) then \(du/dx=5x^{4}\) and \(x^{4}=\frac{1}{5}du/dx\). Substituting in the integral we get: \[\begin{align*} \int\frac{x^{4}}{1+x^{5}}dx & =\int\frac{1}{5}du/dx\frac{1}{u}dx\\ & =\frac{1}{5}\int du/dx\frac{1}{u}dx\\ & =\frac{1}{5}\int\frac{1}{u}du\\ & =\frac{1}{5}\ln\left|u\right|+c,\;c\textrm{ a constant}\\ & =\frac{1}{5}\ln\left|1+x^{5}\right|+c. \end{align*}\]

Definite integrals

The method of substitution may also be used to evaluate definite integrals but you need to be careful with the limits of integration when you change the variable of integration.

For example suppose we want to evaluate \(\int_{0}^{1}\left(2x+1\right)^{5}dx\). We set \(u=2x+1\)5 We will use the fact that \[ \left(2x+1\right)^{5}=1\times\left(2x+1\right)^{5}. \] then \(du/dx=2\)and so \(1=\frac{1}{2}\frac{du}{dx}\). Note that when \(x=0,\) \(u=1\) and when \(x=1,\) \(u=3.\) Substituting into the integral we get: \[\begin{align*} \int_{0}^{1}\left(2x+1\right)^{5}dx & =\int_{0}^{1}1.\left(2x+1\right)^{5}dx\\ & =\int_{0}^{1}\frac{1}{2}\frac{du}{dx}.u^{5}dx\\ & =\frac{1}{2}\int_{1}^{3}u^{5}du\\ & =\frac{1}{2}\frac{1}{6}\left[u^{6}\right]_{u=1}^{u=3}\\ & =\frac{1}{12}\left(3^{6}-1^{6}\right)\\ & =\frac{1}{12}\left(729-1\right)\\ & =\frac{728}{12}\\ & =\frac{182}{3}. \end{align*}\] Note the change of limits on the integration in line 3 as we are now integrating with respect to \(u.\)

Alternative Notation

In many texts and possibly your lecture notes, you will find a slight change in notation. For example, consider the integral of Example 1 above: \(\int2x\cos\left(x^{2}\right)dx.\) As before we set \(u=x^{2}\) then \(du/dx=2x\). The alternative notation then rearranges this to give \(dx=\frac{1}{2x}du\). Then substituting for \(x^{2}\) and \(dx\) in the integral we get: \[\begin{align*} \int2x\cos\left(x^{2}\right)dx & =\int2x\cos\left(u\right)\frac{1}{2x}du\\ & =\int\cos\left(u\right)du\\ & =\sin\left(u\right)+c,\;c\textrm{ a constant}\\ & =\sin\left(x^{2}\right)+c. \end{align*}\] This method gives the same result and will always work. However, you should realize that \(du/dx\) is not a fraction6 The derivative \(du/dx\) is not a fraction. Remember that the derivative of a function \(u\left(x\right)\)is defined by the limit: \[\begin{align*} \frac{du}{dx} & =\lim_{h\rightarrow0}\frac{u\left(x+h\right)-u\left(x\right)}{h}. \end{align*}\] and you have no right to treat it like one when you rewrite \(du/dx\) as \(dx=\frac{1}{2x}du\).

Exercises

Find the following:

  1. \(\int\left(5x+1\right)^{4}dx\)

  2. \(\int3x^{2}\left(x^{3}+2\right)^{5}dx\)

  3. \(\int\left(2x+1\right)\left(x^{2}+x+3\right)^{3}dx\)

  4. \(\int6x^{2}\sqrt{\left(x^{3}+3\right)}dx\)

  5. \(\int\sin\left(3x+2\right)dx\)

  6. \(\int6x^{2}e^{x^{3}}dx\)

  7. \(\int\frac{2x}{2+x^{2}}dx\)

Answers

In the answers below, \(c\) is a constant.

  1. \(\frac{\left(5x+1\right)^{5}}{25}+c\)

  2. \(\frac{\left(x^{3}+2\right)^{6}}{6}+c\)

  3. \(\frac{\left(x^{2}+x+3\right)^{4}}{4}+c\)

  4. \(\frac{4\left(x^{3}+3\right)^{3/2}}{3}+c\)

  5. \(-\frac{1}{3}\cos\left(3x+2\right)+c\)

  6. \(2e^{x^{3}}+c\)

  7. \(\ln\left(2+x^{2}\right)+c\)

Download this page, IN6:Integration by Substitution (PDF 164 KB)

What's next... IN7 Integration using partial fractions

Keywords: 
Maths
Integration