IN3.1 Integration of functions of the form m over (ax+b)
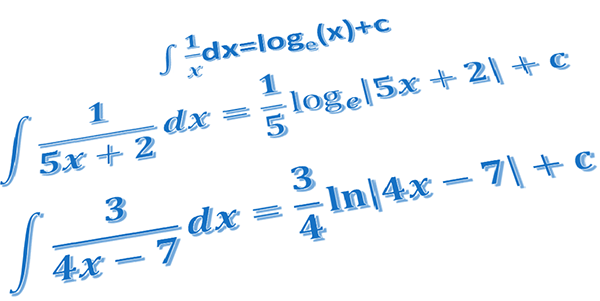
How do you integrate a logarithm? How do you integrate an exponential function? How do you integrate a trigonometric function? Read this worksheet to see how this is done.
This module looks at integrals such as \(\int\frac{1}{x}dx\) and\(\int\frac{1}{3x-1}dx.\)
The Power Rule for Integration
One of the most important rules for integration is the power rule which says:1 Note that if \(n=-1\), \({\textstyle 1/(n+1)}\) would be \({\textstyle 1/0}\) which has no meaning. \(n\) can be any number (other than \(-1\)) - positive, negative or a fraction. Instead of saying c is a constant, we sometimes write \(c\in\mathbb{R}\) which means \(c\) is a real number.
Provided \(n\neq-1\) then \[ \int x^{n}dx=\frac{1}{n+1}x^{n+1}+c \] where \(c\) is a constant.
For example: \[\begin{align*} \int xdx & =\frac{1}{2}x^{2}+c,\quad c\in\mathbb{R}\\ \int x^{2}dx & =\frac{1}{3}x^{3}+c,\quad c\in\mathbb{R} \end{align*}\]
The question is, " How do we deal with the case when \(n=-1\). That is, how do we integrate \(\int\left(1/x\right)dx\,\)? The answer is we define a new function as follows:
\[ \int\frac{1}{x}dx=\log_{e}\left|x\right|+c\textrm{$\quad\textrm{where c is a constant.}$ } \] This function, \(\log_{e}\left|x\right|\), is called the “natural logarithm”. It is sometimes written as \(\textrm{ln$\left|x\right|$ }\). Note the use of the absolute value sign. The natural logarithm is not defined for negative arguments.
We can now integrate \(f(x)=m/x\) where \(m\) is any constant: \[\begin{align*} \int\frac{m}{x}dx & =m\int\frac{1}{x}dx\\ & =m\log_{e}\left|x\right|+c \end{align*}\]
For example, the integral of \(f(x)=\frac{5}{x}\) with respect to \(x\) is \(\int\frac{5}{x}dx=5\log_{e}\left|x\right|+c\quad c\in\mathbb{R}.\) There is a more general rule which covers more cases. It is:
Let \(a\) , b and \(m\) be constants with \(a\neq0\), then \[ \int\frac{m}{ax+b}dx=\frac{m}{a}\log_{e}\left|ax+b\right|+c \] where \(c\) is a constant.
Examples
Integrate \(f(x)=\frac{1}{2x}\:\)with respect to \(x.\;\)2 Here, \(m=1\), \(a=2\) and \(b=0\).
Solution: Using the rule \[\begin{align*} \int\frac{1}{2x}dx & =\frac{1}{2}\log_{e}\left|2x\right|+c,\quad c\in\mathbb{R}. \end{align*}\]Calculate the integral \(\int\frac{2}{3x}dx\) \(\;\,\)3 Here, \(m=2\), \(a=3\) and \(b=0\).
Solution: Using the rule \[\begin{align*} \int\frac{2}{3x}dx & =\frac{2}{3}\log_{e}\left|3x\right|+c,\quad c\in\mathbb{R}. \end{align*}\]Integrate \(f(x)=\frac{13}{5x-7}\) with respect to \(x.\;\) 4 Here, \(m=13\), \(a=5\) and \(b=-7\).
Solution: Using the rule \[\begin{align*} \int\frac{13}{5x-7}dx & =\frac{13}{5}\textrm{ln}\left|5x-7\right|+c,\quad c\in\mathbb{R}. \end{align*}\]Integrate \(f(x)=\frac{6}{2-3x}\) with respect to \(x.\;\) 5 Here, \(m=6\), \(a=-3\) and \(b=2\).
Solution: Using the rule \[\begin{align*} \int\frac{6}{2-3x}dx & =\frac{6}{-3}\log_{e}\left|2-3x\right|+c,\quad c\in\mathbb{R}\\ & =-2\log_{e}\left|2-3x\right|+c. \end{align*}\]Integrate \(f(x)=\frac{6}{2-3x}-\frac{2}{x+1}\) with respect to \(x.\;\) 6 Here, \(m=6\), \(a=-3\) and \(b=2\) in the first term on the right hand side and \(m=-2\), \(a=1\) and \(b=1\)in the second.
Solution: Using the rule \[\begin{align*} \int\left(\frac{6}{2-3x}-\frac{2}{x+1}\right)dx & =\frac{6}{-3}\log_{e}\left|2-3x\right|-2\log_{e}\left|x+1\right|+c,\quad c\in\mathbb{R}\\ & =-2\log_{e}\left|2-3x\right|-2\log_{e}\left|x+1\right|+c \end{align*}\]
Exercises
- Calculate the following integrals
\[ \begin{array}{cccccccccccc} a) & \int\frac{1}{5x}dx & & b) & \int\frac{3}{2x}dx & & c) & \int\frac{3}{3x-5}dx & & d) & \int\frac{6}{2-7x}dx\end{array} \]
- Integrate the following functions with respect to \(x\):
\[ \begin{array}{cccccccccccc} a) & f(x)=x^{2}-2/x & & b) & f(x)=\frac{1}{3x-2}+\frac{3}{1-x} & & c) & f(x)=\frac{3}{3x-7}-x^{2} & & d) & f(x)=\frac{2}{5x-4}-\frac{3}{2-5x}\end{array} \]
\[ \begin{array}{cccccccccc} 1a) & \frac{1}{5}\log_{e}\left|x\right|+c & & & 1b) & \frac{3}{2}\log_{e}\left|2x\right|+c & & & 1c) & \frac{3}{2}\log_{e}\left|2x-7\right|+c\\ 1d) & -\frac{6}{7}\log_{e}\left|2-7x\right|+c\\ \\ \\ 2a) & \frac{1}{3}x^{3}-2\log_{e}\left|x\right|+c & & & 2b) & \frac{1}{3}\log_{e}\left|3x-2\right|-3\log_{e}\left|1-x\right|+c & & & 2c) & \log\left|3x-5\right|+c\\ 2d) & \frac{2}{5}\log_{e}\left|5x-4\right|+\frac{3}{2}\log_{e}\left|2-5x\right|+c \end{array} \]
The Definite Integral
Answers to all the integrals above were functions of \(x\) and involved a constant. Such integrals are called indefinite integrals or antiderivatives. They do not have a specific value.
For a function \(f(x)\) suppose we can write an antiderivative \(F(x)=\int f(x)dx\). We then define a definite integral of a function \(f(x)\) from \(a\) to \(b\) with respect to \(x\) using the notation:7 This is known as the first fundamental theorem of calculus. \[ \int_{a}^{b}f(x)dx=\left[F(x)\right]_{a}^{b}=F(b)-F(a) \] where we assume \(f(x)\) is defined for all \(x\) in the interval \([a,b]\). We call \(a\) the lower limit of integration and \(b\) the upper limit of integration. The notation \(\left[F(x)\right]_{a}^{b}\) means substitute \(x=b\) and \(x=a\) into \(F(x)\) and then subtract the values. This gets rid of the constant of integration \(c\).
For example, suppose we want to find, \(\intop_{1}^{3}xdx.\) Then 8 First we find an antiderivative or indefinite integral \(\int xdx+c\) and then evaluate this at the limits of integration. \[\begin{align*} F(x) & =\int xdx\\ & =\left[\frac{1}{2}x^{2}+c\right]_{x=1}^{x=3},\quad c\in\mathbb{R}\\ & =\left(\frac{1}{2}3^{2}+c\right)-\left(\frac{1}{2}1^{2}+c\right)\\ & =\left(\frac{9}{2}+c\right)-\left(\frac{1}{2}+c\right)\\ & =\frac{8}{2}\\ & =4. \end{align*}\] Note that the indefinite integral has a numerical value, in this case \(4\), and there is no constant \(c\).
Examples
Find the integral \(\int_{1}^{2}\frac{1}{2x}dx\). 9 In this case the antiderivative is \(F(x)=\frac{1}{2}\log_{e}\left|2x\right|+c,\quad c\in\mathbb{R}.\) Also remember the log laws: \[\begin{align*} \log b-\log a & =\log\frac{b}{a}\\ \log b+\log a & =\log\left(ba\right). \end{align*}\]
Solution: \[\begin{align*} \int_{1}^{2}\frac{1}{2x}dx & =\left[\frac{1}{2}\log_{e}\left|2x\right|+c\right]_{x=1}^{x=2}\\ & =\frac{1}{2}\log_{e}\left|2(2)\right|+c-\left(\frac{1}{2}\log_{e}\left|2\left(1\right)\right|+c\right)\\ & =\frac{1}{2}\log_{e}\left|4\right|-\frac{1}{2}\log_{e}\left|2\right|\\ & =\frac{1}{2}\log_{e}\left|\frac{4}{2}\right|\\ & =\frac{1}{2}\log_{e}2. \end{align*}\] Note that it is not usual to include the constant \(c\) as we did in lines 1 and 2 of the solution above. The next example shows this.Find the integral \(\int_{2}^{3}\frac{13}{5x-7}dx\). 10 In this case the antiderivative is \(F(x)=\frac{13}{5}\log_{e}\left|5x-7\right|+c,\quad c\in\mathbb{R}.\)
Solution: \[\begin{align*} \int_{2}^{3}\frac{13}{5x-7}dx & =\left[\frac{13}{5}\log_{e}\left|5x-7\right|\right]_{2}^{3}\\ & =\frac{13}{5}\log_{e}\left|15-7\right|-\left(\frac{13}{5}\log_{e}\left|10-7\right|\right)\\ & =\frac{13}{5}\log_{e}\left|8\right|-\left(\frac{13}{5}\log_{e}\left|3\right|\right)\\ & =\frac{13}{5}\log_{e}\frac{8}{3}. \end{align*}\]
Exercises:
Find the integral \(\int_{1}^{5}\frac{2}{3x}dx\).
Calculate the integral \(\int_{1}^{2}\frac{2}{3x-1}dx\)
Find the integral \(\int_{1}^{3}\left(x^{2}-2/x\right)dx.\) Hint: \(\log_{e}1=0.\)
\(\int_{2}^{4}\left(\frac{2}{5x-4}-\frac{3}{2-5x}\right)dx.\) Hint: \(\log_{e}1=0.\)
\(2\log_{e}5\) or \(\log_{e}25\) (using log law \(a\log_{e}x=\log_{e}x^{a}\).
\(\frac{2}{3}\log_{e}3\).
\(\frac{26}{3}-2\textrm{ln}3\).
\(\frac{2}{5}\textrm{ln}\frac{8}{3}+\frac{3}{5}\textrm{ln}\frac{9}{4}\).
Download this page, IN3.1 Integration of functions of the form m over (ax+b) (PDF 230 KB)
What's next... IN3.3 Integration of exponential functions
