IN2 Integration of polynomials
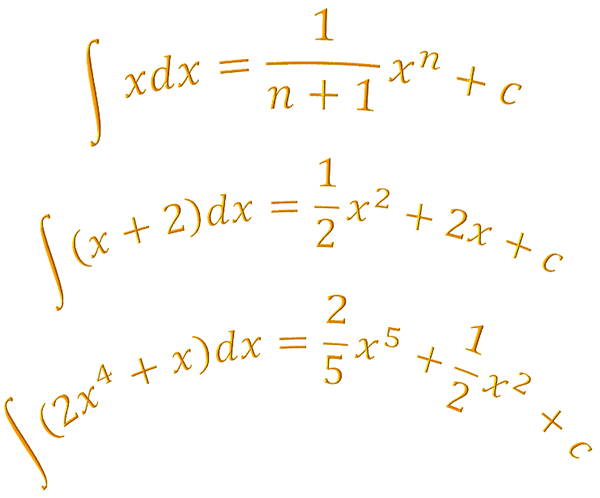
How do you integrate a polynomial where x is raised to a power? We saw this in the previous section on antidifferentiation. But how do you integrate a linear expression in brackets where the whole bracket is raised to a power? This worksheet will show you how.
This module shows how to integrate functions like : \[ f\left(x\right)=2x^{4}-3x+2 \] or more generally: \[ f\left(x\right)=a_{0}+a_{1}x+a_{2}x^{2}+\cdots+a_{n}x^{n} \] where \(a_{i},\,i=1,2,3,\ldots,n\) are constants. Such functions are called polynomials.
Antidifferentiation
Antidifferentiation is the opposite process to differentiation. For example if \(y=x^{2}\), then an antiderivative of \(y\) is \(\frac{1}{3}x^{3}\) because the derivative of \(\frac{1}{3}x^{3}\) is \(y\). A mathematical notation for this is \[ \int x^{2}dx=\frac{1}{3}x^{3}+c,\textrm{ where $c$ is a constant}. \] This is read as “the indefinite integral of \(x^{2}\) with respect to \(x\) is equal to \(\frac{1}{3}x^{3}+c\)”. The \(\int\) sign means indefinite integral and \(dx\) means with respect to \(x\). Here the words “indefinite integral” are the same as “antiderivative”.
Integration is more complicated than differentiation. However there are some rules to help us. One of the most important is the power rule which says:1 Note that if \(n=1\), \({\textstyle 1/(n-1)}\) would be \({\textstyle 1/0}\) which has no meaning. \(n\) can be any number (other than 1) - positive, negative or a fraction. Instead of saying c is a constant, we sometimes write \(c\in\mathbb{R}\) which means \(c\) is a real number.
Provided \(n\neq1\) then (x{n}dx=x{n+1}+c,)
Examples \[\begin{align*} \int xdx & =\frac{1}{2}x^{2}+c,\quad c\in\mathbb{R}\\ \int x^{2}dx & =\frac{1}{3}x^{3}+c,\quad c\in\mathbb{R} \end{align*}\]
Linearity
The integral has two properties that let us evaluate more complex functions. They are called the linearity rules:
A constant that multiplies a function may be taken out of the integral. For a constant \(a\) and functions \(f\left(x\right)\) and \(g\left(x\right)\) \[ \int af\left(x\right)dx=a\int f\left(x\right)dx \]
and \[\begin{align*} \int\left(f\left(x\right)+g\left(x\right)\right)dx & =\int f\left(x\right)dx+\int g\left(x\right)dx\\ \int\left(f\left(x\right)-g\left(x\right)\right)dx & =\int f\left(x\right)dx-\int g\left(x\right)dx. \end{align*}\]
Examples
Integrate the constant \(3\).
Solution:2 Note that \(3=3x^{0}.\) In fact, any constant \(m\) can be written as \(mx^{0}\) \[\begin{align*} \int3dx & =\int3x^{0}dx\\ & =3\int x^{0}dx\quad\textrm{ by linearity}\\ & =3x+c,\, \textrm{$c$ a constant, using the power rule.} \end{align*}\]Find \(\int5xdx\).
Solution: \[\begin{align*} \int5xdx & =5\int xdx\quad\textrm{by linearity}\\ & =\frac{5}{2}x^{2}+c,\, \textrm{$c$ a constant, using the power rule}. \end{align*}\]Find \(\int\left(5x^{2}-3x+4\right)dx.\)
Solution:3 Note there is a constant for each of the integrals on the right hand side. However, a constant plus a constant still gives you a constant so we just use a single constant \(c\in\mathbb{R}.\) \[\begin{align*} \int\left(5x^{2}-3x+4\right)dx & =\int5x^{2}dx+\int\left(-3x\right)dx\\ & \quad\quad+\int4dx\ \textrm{ using linearity}\\ & =5\int x^{2}dx-3\int\,xdx+4\quad\int dx\ \textrm{ using linearity}\\ & =\frac{5}{3}x^{3}-\frac{3}{2}x^{2}+4x+c,\, \textrm{$c$ a constant, using the power rule.} \end{align*}\]
Note that you can have any number of terms in the integral. For example if \(a_{1},a_{2},a_{3}\ldots a_{n}\) are constant \[\begin{align*} \int\left(a_{0}+a_{1}x+a_{2}x^{2}+\ldots+a_{n}x^{n}\right)dx & =\int a_{0}dx+\int a_{1}xdx+\int a_{2}x^{2}+\ldots+\int a_{n}x^{n}dx\\ & =a_{0}x+a_{1}\int xdx+a_{2}\int x^{2}+\ldots+a_{n}\int x^{n}dx. \end{align*}\]
Examples
Integrate \(f(x)=13x^{2}+x+5\) with respect to \(x\).
Solution: \[\begin{align*} \int\left(13x^{2}+x+5\right)dx & =\frac{13}{3}x^{3}+\frac{1}{2}x^{2}+5x+c\quad c\in\mathbb{R}. \end{align*}\]Integrate \(f\left(y\right)=4y^{5}-y^{3}\) with respect to \(y\).
Solution: \[\begin{align*} \int\left(4y^{5}-y^{3}\right)dy & =\int4y^{5}dy-\int y^{3}dy\\ & =\frac{4}{6}y^{6}+\frac{1}{4}y^{4}+c\quad\textrm{where }c\textrm{ is a constant}\\ & =\frac{2}{3}y^{6}+\frac{1}{4}y^{4}+c \end{align*}\]Integrate \(f(x)=2x^{7}+2x^{2}-x-3\) with respect to \(x\).
Solution: \[\begin{align*} \int\left(2x^{7}+2x^{2}-x-3\right)dx & =\int2x^{7}dx+\int2x^{2}dx-\int xdx-\int3dx\\ & =\frac{2}{8}x^{8}+\frac{2}{3}x^{3}-\frac{1}{2}x^{2}-3x+c\quad\textrm{where }c\textrm{ is a constant}\\ & =\frac{1}{4}x^{8}+\frac{2}{3}x^{3}-\frac{1}{2}x^{2}-3x+c. \end{align*}\]
Exercises
Integrate the following with respect to \(x\):
\[\begin{array}{cccccccccccc} a) & x^{3} & & b) & x^{3}-2x & & c) & 2x^{4}+5x^{2} & & d) & 3x^{2}-7x^{5}\\ \\ e) & x^{2}-2+x & & f) & 2x+2 & & g) & -6x^{3}+5x+2 & & h) & 9x^{6}-3x-4 \end{array}\]
\[\begin{array}{cccccccccccccc} a) & \frac{1}{4}x^{4}+c & & & b) & \frac{1}{4}x^{4}-x^{2}+c & & & c) & \frac{2}{5}x^{5}+\frac{5}{3}x^{3}+c & & & d) & x^{3}-\frac{7}{6}x^{6}+c\end{array}\]
\[\begin{array}{cccccccccccccc} e) & \frac{1}{3}x^{3}-2x+\frac{1}{2}x^{2}+c & & & f) & x^{2}+2x+c & & & g) & -\frac{3}{2}x^{4}+\frac{5}{2}x^{2}+2x+c & & & h) & \frac{9}{7}x^{7}-\frac{3}{2}x^{2}-4x+c\end{array}\]
The Definite Integral
Answers to all the examples above were functions of \(x\) and involved a constant. Such integrals are called indefinite integrals or antiderivatives. They do not have a specific value.
For a function \(f(x)\) suppose we can write an antiderivative \(F(x)=\int f(x)dx\). We then define a definite integral of a function \(f(x)\) from \(a\) to \(b\) with respect to \(x\) using the notation:4 This is known as the first fundamental theorem of calculus. \[ \int_{a}^{b}f(x)dx=\left[F(x)\right]_{a}^{b}=F(b)-F(a) \] where we assume \(f(x)\) is defined for all \(x\) in the interval \([a,b]\). We call \(a\) the lower limit of integration and \(b\) the upper limit of integration. The notation \(\left[F(x)\right]_{a}^{b}\) means substitute \(x=b\) and \(x=a\) into \(F(x)\) and then subtract the values. This gets rid of the constant of integration \(c\).
Examples of Definite Integrals
Suppose we want to find, \(\intop_{1}^{3}xdx.\) Then 5 First we find an antiderivative or indefinite integral \(\int xdx+c\) and then evaluate this at the limits of integration. An antiderivative is \(\frac{1}{2}x^{2}+c\). \[\begin{align*} \int_{1}^{3}xdx & =\left[\frac{1}{2}x^{2}+c\right]_{x=1}^{x=3},\quad c\in\mathbb{R}\\ & =\left(\frac{1}{2}3^{2}+c\right)-\left(\frac{1}{2}1^{2}+c\right)\\ & =\left(\frac{9}{2}+c\right)-\left(\frac{1}{2}+c\right)\\ & =\frac{8}{2}\\ & =4. \end{align*}\] Note that the indefinite integral has a numerical value, in this case \(4\), and there is no constant \(c\).
Calculate \(\intop_{0}^{4}\left(x^{3}-6x^{2}+x-2\right)dx\).
Solution: \[\begin{align*} \intop_{0}^{4}\left(x^{3}-6x^{2}+x-2\right)dx & =\left[\frac{1}{4}x^{4}-2x^{3}+\frac{1}{2}x^{2}-2x\right]_{x=0}^{x=4}\\ & =\frac{1}{4}\left(4^{4}\right)-2\left(4^{3}\right)+\frac{1}{2}\left(4^{2}\right)-2\left(4\right)\\ & =4^{3}-2\left(64\right)+\frac{1}{2}\left(16\right)-8\\ & =-64 \end{align*}\]Evaluate \(\int_{-1}^{2}\left(5x^{3}-2x^{2}\right)dx\).
Solution: \[\begin{align*} \intop_{-1}^{2}\left(5x^{3}-2x^{2}\right)dx & =\left[\frac{5}{4}x^{4}-\frac{2}{3}x^{3}\right]_{x=-1}^{x=2}\\ & =\frac{5}{4}\left(2^{4}\right)-\frac{2}{3}\left(2^{3}\right)-\left(\frac{5}{4}\left(-1\right)^{4}-\frac{2}{3}\left(-1\right)^{3}\right)\\ & =\frac{5}{4}\left(16\right)-\frac{2}{3}\left(8\right)-\left(\frac{5}{4}+\frac{2}{3}\right)\\ & =20-\frac{16}{3}-\frac{23}{12}\\ & =\frac{153}{12}\\ & =\frac{51}{4} \end{align*}\]
Exercises on Definite Integrals
Evaluate the following indefinite integrals:
\[\begin{array}{lllll} a) \int_{1}^{2}\left(6x-2\right)dx & & b) \int_{2}^{3}\left(8x^{3}-9x^{2}-2x\right)dx & & c) \int_{0}^{2}\left(7x^{2}+2\right)dx\\ & & & & \\ d) \int_{-1}^{2}\left(7x^{3}-6x+3\right)dx & & e) \int_{-1}^{1}\left(8x^{3}-x^{2}+6\right)dx & & f) \int_{-1}^{0}\left(8x^{3}-x^{2}+6\right)dx\\ \end{array}\]
\[\begin{array}{lllllllllll} a) 7 & & b) 68 & & c) 69 & & d) 105/4 & & e) 38/3 & & f) 11/3\\ \end{array}\]
Download this page, IN2:Integration of Polynomials (PDF 173KB)
What's next... IN3.1 Integration of Functions of the Form m over (ax+b)
