IN5 Area under a curve

August 11, 2022 - 3:41pm — AJ (e67821)

Open image

An area under a curve might be above the axis (and therefore positive). But sections might also be below the axis (and therefore negative). Read this worksheet to see how to deal with finding the integral for sections of graph which go above and below the x-axis (horizontal axis).

This module deals with the problem of finding the area between a curve and the x-axis.

Determining the Area Under a Curve

For a curve defined by \(y=f\left(x\right)\) the definite integral \[ \int_{a}^{b}f\left(x\right)dx \] gives a signed measure of the area bordered by the lines \(x=a\), \(x=b\), \(y=0\) and the graph of \(f\left(x\right)\).11 Note that the line \(y=0\) is the \(x\)-axis.

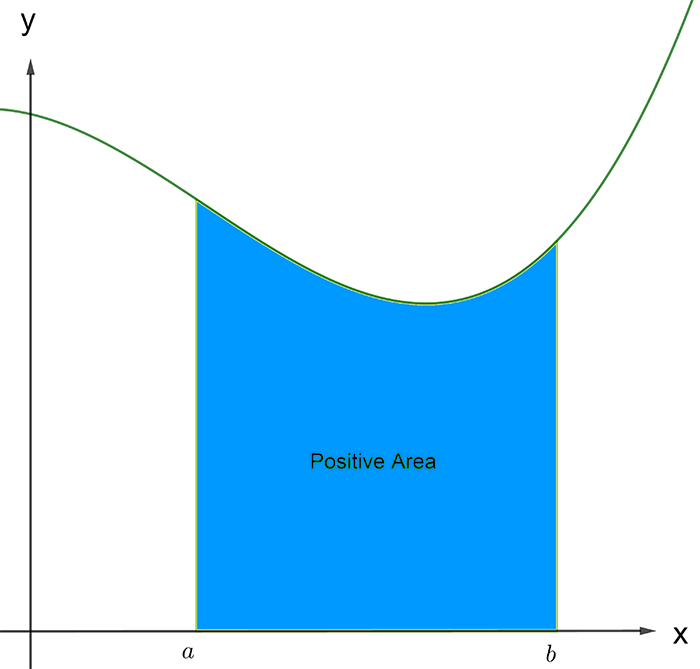
If \(f\left(x\right)\geq0\) between \(x=a\) and \(x=b\) you would get a positive value for the definite integral as shown below.

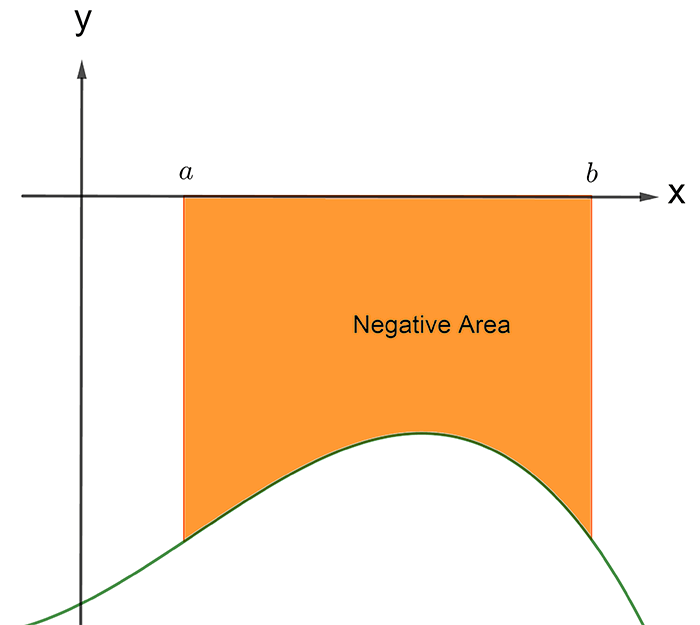
If, \(f\left(x\right)\leq0\) between \(x=a\) and \(x=b\) you would get a negative value for the definite integral as shown below.

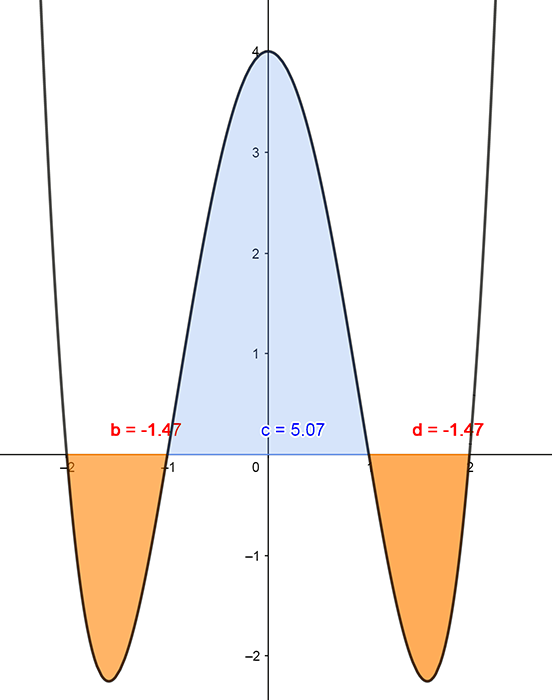
Note that the area under a curve is always given as a positive number. The area is the absolute value of the signed areas: \[ \textrm{Area }=\left|\int_{a}^{b}f\left(x\right)dx\right|. \] In the general case where \(f\left(x\right)\) crosses the \(x\)-axis between \(a\) and \(b\) the value of the definite integral may be positive or negative. However the area under the curve is always taken as the sum of the modulus of the signed areas. For example, the function \(f\left(x\right)=x^{3}-x^{2}-2x\) is plotted below. The graph cuts the \(x\)-axis at -1, 0 and 2.

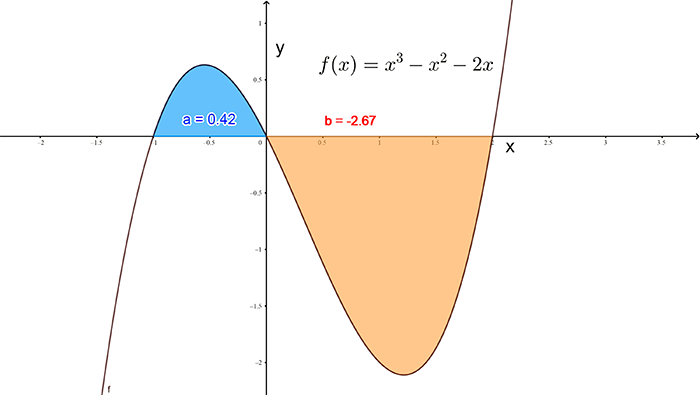
Note that the value of the definite integral from \(x=-1\) to \(x=2\) is \[\begin{align*} \int_{-1}^{2}\left(x^{3}-x^{2}-2x\right)dx & =\left[\frac{1}{4}x^{4}-\frac{1}{3}x^{3}-x^{2}\right]_{x=-1}^{x=2}\\ & =\frac{1}{4}2^{4}-\frac{1}{3}2^{3}-2^{2}-\left(\frac{1}{4}\left(-1\right)^{4}-\frac{1}{3}\left(-1\right)^{3}-\left(-1\right)^{2}\right)\\ & =4-\frac{8}{3}-4-\left(\frac{1}{4}+\frac{1}{3}-1\right)\\ & =-2.25. \end{align*}\] But this is not the area. To calculate the area we need to evaluate two integrals. One from -1 to 0 (this is represented by the blue part of the graph) the other from 0 to 2 that represents the negative signed area. The actual area would then be the sum of the absolute value of these integrals. That is:

\[\begin{align*} \textrm{Area} & =\left|\int_{-1}^{0}\left(x^{3}-x^{2}-2x\right)dx\right|+\left|\int_{0}^{2}\left(x^{3}-x^{2}-2x\right)dx\right|\\ & =\left|\left[\frac{1}{4}x^{4}-\frac{1}{3}x^{3}-x^{2}\right]_{x=-1}^{x=0}\right|+\left|\left[\frac{1}{4}x^{4}-\frac{1}{3}x^{3}-x^{2}\right]_{x=0}^{x=2}\right|\\ & =\left|0-\left(\frac{1}{4}\left(-1\right)^{4}-\frac{1}{3}\left(-1\right)^{3}-\left(-1\right)^{2}\right)\right|+\left|\frac{1}{4}\left(2\right)^{4}-\frac{1}{3}\left(2\right)^{3}-2^{2}\right|\\ & =\left|-\left(\frac{1}{4}+\frac{1}{3}-1\right)\right|+\left|4-\frac{8}{3}-4\right|\\ & =\left|\frac{1}{4}+\frac{1}{3}-1\right|+\frac{8}{3}\\ & =\frac{5}{12}+\frac{8}{3}\\ & =\frac{37}{12}\;\textrm{square units}. \end{align*}\]

Example 1

Given the function \(f\left(x\right)=4x-x^{2}\) find the area between the graph of the function and the x-axis.

Solution: The first step is to sketch the graph of the function. To do this we determine where the graph of the function cuts the x-axis. This gives us the limits of integration for the definite integral. Factorizing the function we see: \[\begin{align*} 4x-x^{2} & =x\left(4-x\right). \end{align*}\] When the graph of the function cuts the x-axis, \(x\left(4-x\right)=0\) and so \(x=0\) or \(x=4\). That is the x-axis intercepts of the function are at \(x=0\) and \(x=4\). At this point we need to graph the function as shown below:

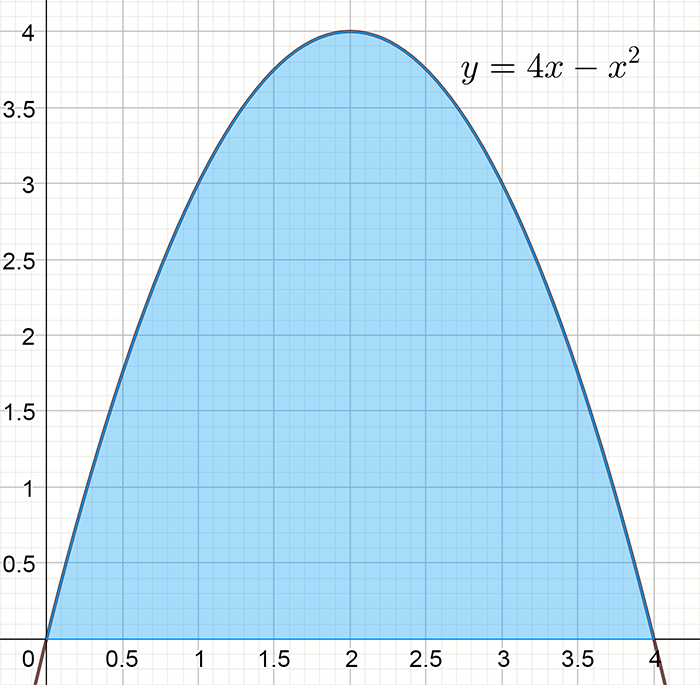
We see the function is above the \(x\)-axis and so the area will be positive.22 Since the area is positive, we do not need the absolute value sign. The area is \[\begin{align*} A & =\int_{0}^{4}f\left(x\right)dx\\ & =\int_{0}^{4}\left(4x-x^{2}\right)dx\\ & =\left[\frac{4x^{2}}{2}-\frac{x^{3}}{3}\right]_{x=0}^{x=4}\\ & =\frac{4\left(4\right)^{2}}{2}-\frac{\left(4\right)^{3}}{3}-\left(\frac{4\left(0\right)^{2}}{2}-\frac{\left(0\right)^{3}}{3}\right)\\ & =\frac{64}{2}-\frac{64}{3}\\ & =\frac{3(64)-2(64)}{6}\\ & =\frac{64}{6}\\ & =\frac{32}{3}\textrm{ square units}. \end{align*}\]

Example 2

Given the function \(f\left(x\right)=x^{2}-1\) find the area bounded by the curve, the \(x\)-axis and the lines \(x=-1\) and \(x=1\).

As in the previous example we need to sketch the graph of the function and then consider the range of integration. Factorizing the function 33 We use \(a^{2}-b^{2}=\left(a-b\right)\left(a+b\right).\) This is an identity you should remember. \[\begin{align*} x^{2}-1 & =\left(x+1\right)\left(x-1\right) \end{align*}\] So the x- axis intercepts where \(f\left(x\right)=x^{2}-1=0\) are \(x=-1\) and \(x=1\). At this point we need to graph the function as shown below:

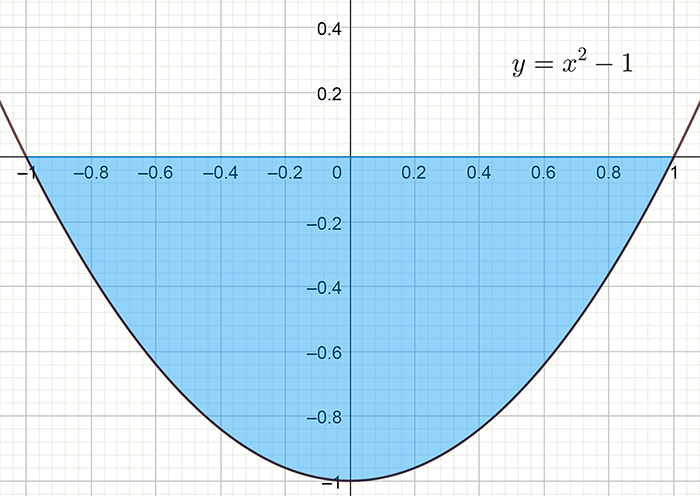
We see the signed area will be negative as \(f\left(x\right)\) is below the axis between the points of integration. So we must use the modulus of the definite integral: \[\begin{align*} \textrm{Area} & =\left|\int_{-1}^{1}\left(x^{2}-1\right)dx\right|\\ & =\left|\left[\frac{1}{3}x^{3}-x\right]_{x=-1}^{x=1}\right|\\ & =\left|\frac{1}{3}-1-\left(\frac{1}{3}\left(-1\right)^{3}-\left(-1\right)\right)\right|\\ & =\left|\frac{1}{3}-1-\left(-\frac{1}{3}+1\right)\right|\\ & =\left|-\frac{2}{3}-\frac{2}{3}\right|\\ & =\left|-\frac{4}{3}\right|\\ & =\frac{4}{3}\;\textrm{square units}. \end{align*}\]

Example 3.

Given the function \(f\left(x\right)=x^{2}-1\) find the area bounded by the curve, the \(x\)-axis and the lines \(x=0\) and \(x=2\). This is the same function as in Example 2 above. First we graph the function:

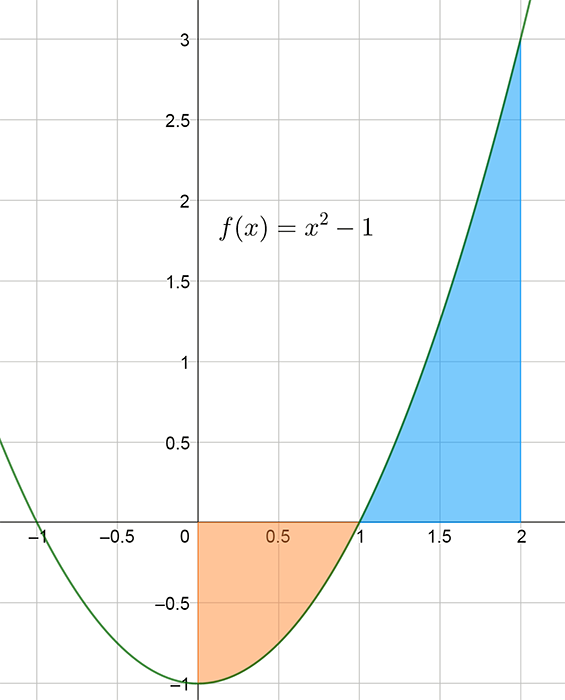
As the function crosses the x-axis between 0 and 2, we will have to evaluate two integrals. The first from 0 to 1 and the second from 1 to 2. \[\begin{align*} \textrm{Area} & =\left|\int_{0}^{1}\left(x^{2}-1\right)dx\right|+\left|\int_{1}^{2}\left(x^{2}-1\right)dx\right|\\ & =\left|\left[\frac{1}{3}x^{3}-x\right]_{x=0}^{x=1}\right|+\left|\left[\frac{1}{3}x^{3}-x\right]_{x=1}^{x=2}\right|\\ & =\left|\frac{1}{3}-1\right|+\left|\frac{8}{3}-2-\left(\frac{1}{3}-1\right)\right|\\ & =\left|-\frac{2}{3}\right|+\left|\frac{8}{3}-\frac{6}{3}-\left(-\frac{2}{3}\right)\right|\\ & =\frac{2}{3}+\frac{2}{3}+\frac{2}{3}\\ & =2\;\textrm{square units}. \end{align*}\]

Exercises

Find the area enclosed by the curve \(y=6x-x^{2}\) and the \(x\)-axis.
Find the area bounded by the curve \(y=\sin(x)\), the \(x\) – axis and the line \(x=\frac{\pi}{2}\).
Find the area bounded by the curve \(y=x^{2}-3x+2\) and the x – axis between \(x=0\) and \(x=2\) .