Skip to content
RMIT University Library - Learning Lab

IN9 Double integrals

 
August 11, 2022 - 3:17pm — AJ (e67821)

Surface f equals a function of x and y, over a region of integration R.

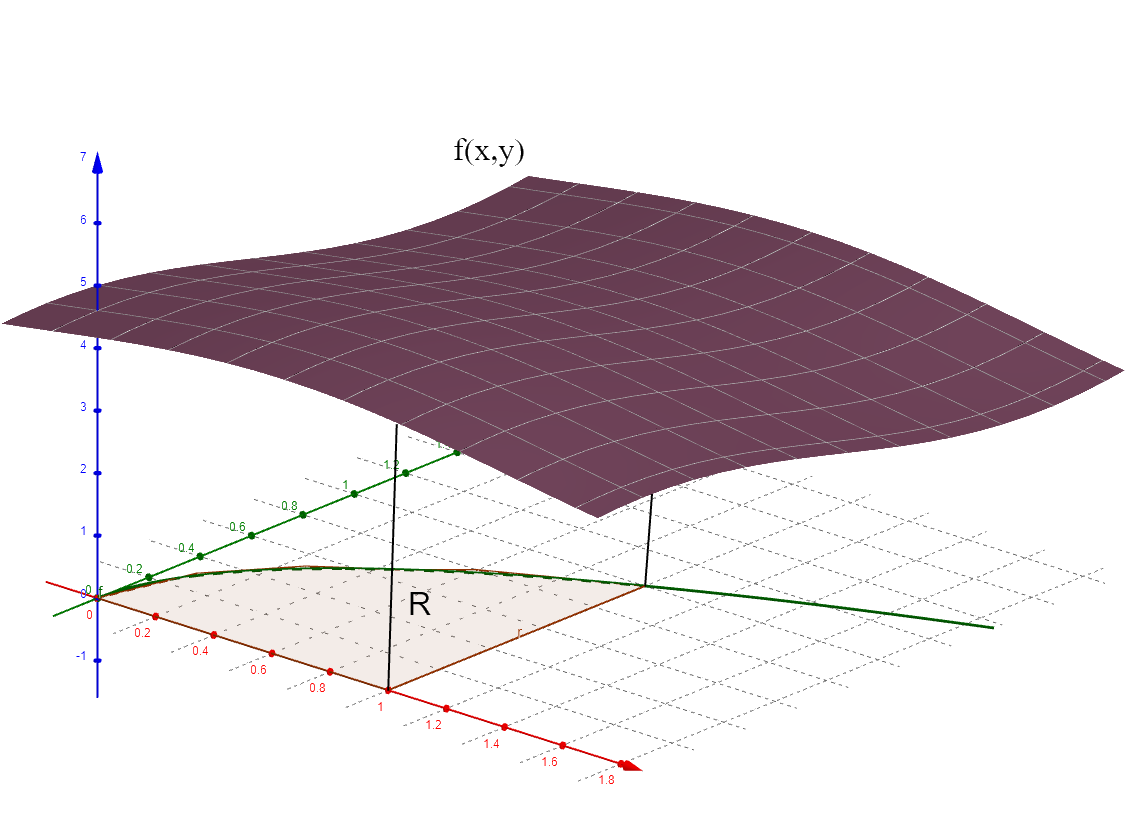
Integrating will find the area between the curve and the x-axis (horizontal axis). We've learned how to limit this to a section of the x axis. But what if you have an area that is bounded by limits on both the x and the y axes? You will need to integrate with respect to the x axis and then integrate with respect to the y axis as well.

Double Integrals is the method you will need. Read this worksheet for some examples and exercises. There are linear, exponential and trigonometric functions defining boundaries for shapes on the x-y axes.

A double integral is of the form:

\[\begin{align*} \underset{R}{\iint}f(x,y)\:dA & =\underset{R}{\iint}f(x,y)\:dx\:dy=\underset{R}{\iint}f(x,y)\:dy\:dx \end{align*}\] where

  • \(z=f(x,y)\) is a continuous function on the region \(R\);

  • \(R\) is a region of integration in the \(x\)-\(y\) plane;

  • \(dA\) is an infinitesimal element of area in \(R\) and \(dA=dx\:dy=dy\:dx\). If \(f(x,y)\geq0\) then the double integral is equal to the volume below the surface \(f(x,y)\) and above the region \(R\).

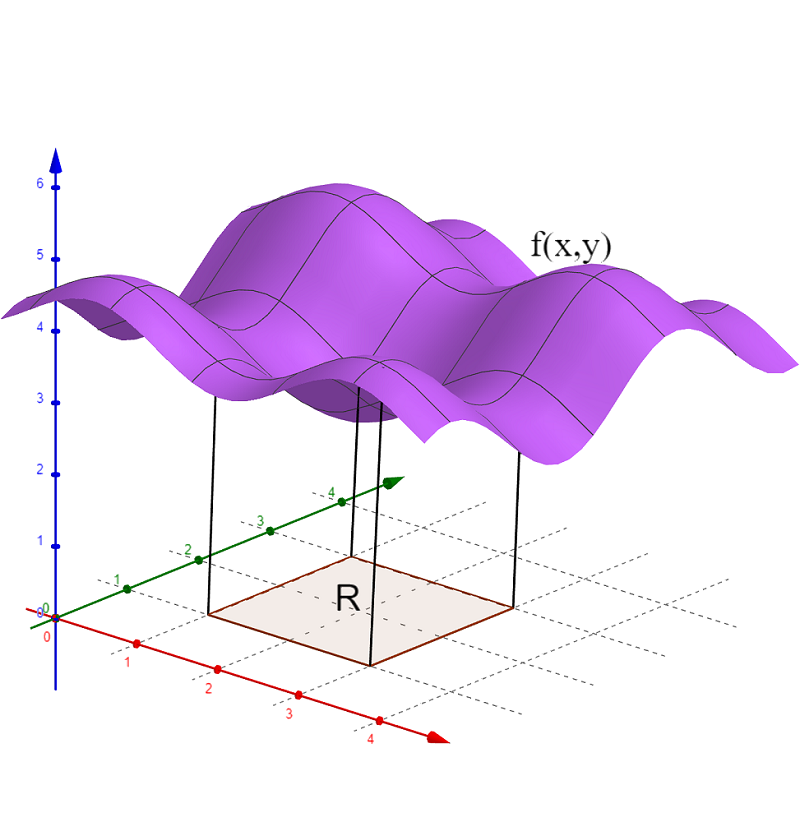
Surface f equals a function of x and y, over a region of integration R.

Evaluation

A double integral may be evaluated in two ways:

  • Integrating first with respect to \(x\), keeping \(y\) constant.
    If \(a\leq x\leq b\) and \(c\leq y\leq d\) , the integral becomes \(\underset{R}{\iint}f(x,y)\:dA=\int_{c}^{d}\left[\int_{a}^{b}f(x,y)\:dx\right]\:dy\) .
    The “inner” integral is the integral with respect to \(x\) and the “outer” integral is the integral with respect to \(y\) .
  • Integrating first with respect to \(y\), keeping \(x\) constant, with \(a\leq y\leq b\) and \(c\leq x\leq d\) .
    The integral becomes \(\underset{R}{\iint}f(x,y)\:dA=\int_{c}^{d}\left[\int_{a}^{b}f(x,y)\:dy\right]\:dx\) .
    The “inner” integral is the integral with respect to \(y\) and the “outer” integral is the integral with respect to \(x\) . In practice integrating first with respect to \(x\) (or \(y\)) may be easier than integrating first with \(y\) (or \(x\)).

To evaluate a double integral it is helpful to:

  1. Sketch the region of integration;

  2. Determine the limits of integration;

  3. Work out the inner integral, then

  4. Evaluate the outer integral.

Double Integrals Over a Rectangular Region

The easiest case is when the region is a rectangle.

Example 1

Evaluate \(\underset{R}{\iint}(3x^{2}-2xy)\:dx\:dy\) where \(R\) is the rectangle with vertices \((2,1),\) \((2,3),\) \((4,1),\) \((4,3)\) .

Solution:

The region is shown below.

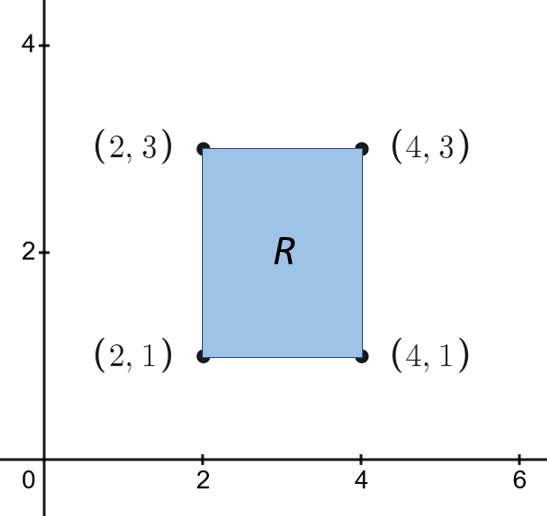
Rectangular region in x y plane.

The limits of integration for the inner integral are \(x=2\) to \(x=4\) .

The limits of integration for the outer integral are \(y=1\) to \(y=3\) .

Thus, the integral becomes: \(\int_{1}^{3}\left[\int_{2}^{4}(3x^{2}-2xy)\:dx\right]\:dy\)

First, we work out the inner integral, integrating with respect to \(x\) while treating \(y\) as a constant.

Then integrate with respect to \(y\) and evaluate.

\[\begin{align*} \int_{1}^{3}\left[\int_{2}^{4}(3x^{2}-2xy)\:dx\right]\:dy & =\int_{1}^{3}\left[\left(\frac{3x^{3}}{3}-\frac{2x^{2}y}{2}\right)_{2}^{4}\right]\:dy\\ & =\int_{1}^{3}\left[\left(x^{3}-x^{2}y\right)_{2}^{4}\right]\:dy\\ & =\int_{1}^{3}\left[\left(4^{3}-4^{2}y\right)-\left(2^{3}-2^{2}y\right)\right]\:dy\\ & =\int_{1}^{3}\left[\left(64-16y\right)-\left(8-4y\right)\right]\:dy\\ & =\int_{1}^{3}\left[56-12y\right]\:dy\\ & =\left[56y-\frac{12y^{2}}{2}\right]_{1}^{3}\\ & =\left[56y-6y^{2}\right]_{1}^{3}\\ & =\left(56(3)-6(3)^{2}\right)-\left(56(1)-6(1)^{2}\right)\\ & =168-54-56+6\\ & =64 \end{align*}\]

In this example you could reverse the order of integration and still obtain the same answer.

Example 2: Reversing the Order of Integration in Example 1

Solution:

In this case, the integral becomes: \(\int_{2}^{4}\left[\int_{1}^{3}(3x^{2}-2xy)\:dy\right]\:dx\)

\[\begin{align*} \int_{2}^{4}\left[\int_{1}^{3}(3x^{2}-2xy)\:dy\right]\:dx & =\int_{2}^{4}\left[\left(3x^{2}y-2x\frac{y^{2}}{2}\right)_{1}^{3}\right]\:dx\\ & =\int_{2}^{4}\left[\left(3x^{2}y-xy^{2}\right)_{1}^{3}\right]\:dx\\ & =\int_{2}^{4}\left[\left(3x^{2}(3)-x(3)^{2}\right)-\left(3x^{2}(1)-x(1)^{2}\right)\right]\:dx\\ & =\int_{2}^{4}\left[\left(9x^{2}-9x\right)-\left(3x^{2}-x\right)\right]\:dx\\ & =\int_{2}^{4}\left[6x^{2}-8x\right]\:dx\\ & =\left[\frac{6x^{3}}{3}-\frac{8x^{2}}{2}\right]_{2}^{4}\\ & =\left[2x^{3}-4x^{2}\right]_{2}^{4}\\ & =\left(2(4)^{3}-4(4)^{2}\right)-\left(2(2)^{3}-4(2)^{2}\right)\\ & =128-64-16+16\\ & =64 \end{align*}\]

As expected the same answer is obtained regardless of the order of integration (provided that the function is continuous over the region of integration).

Exercise 1

  1. Evaluate \(\underset{R}{\iint}(4xy)\:dx\:dy\) where \(R\) is the rectangle with vertices \((0,1),\) \((0,3),\) \((3,1),\) \((3,3)\) .

  2. Evaluate \(\underset{R}{\iint}(6e^{x}+e^{y})\:dy\:dx\) where \(R\) is the region bounded by the lines \(x=0,\) \(x=4,\) \(y=1,\) \(y=2\) .

  3. Evaluate \(\int_{0}^{3}\int_{1}^{4}(\sin\pi x+\cos\pi y)\:dy\:dx\)

  4. Find \(\int_{0}^{b}\int_{0}^{a}(5)\:dx\:dy\) . What is the physical significance of this result?

Answers

\(\text{$$ a. $\text{72$\quad\text{b. $6e^{4}+4e^{2}-4e-6\quad\text{c. $\text{6/$\pi$ }$ }$ }$ }$ }\)

\(\text{d. $5ab.$ This is the volume of a cuboid of height $5,$ length $a$ and width $b.$ }\)

Double Integrals Over a General Region

For a general region of integration the limits of integration are not necessarily constants. Frequently they are functions. It is important to be able to sketch the region to identify the limits of integration.

Example 3

Evaluate \(\underset{R}{\iint}(10x-4y+5)\:dx\:dy\) where \(R\) is the region bounded by the curve \(y=\sqrt{x}\) and the \(x\)- axis, from \(x=0\) to \(x=1\) .

Surface over region R.

Solution:

Firstly, sketch the region of integration on the \(x,\) \(y\) plane.

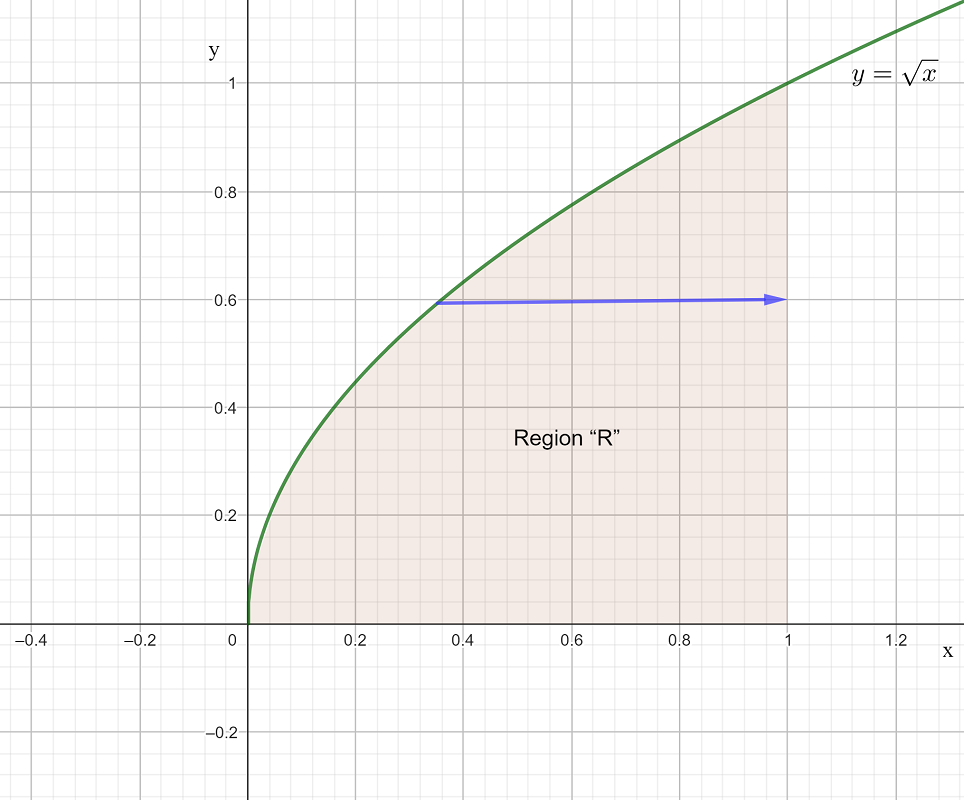
Detail of the region R

Secondly, find the limits of integration.

The “inner” integration is with respect to \(x\) , so we draw an arrow across the region of integration, parallel to the \(x\)-axis (keeping \(y\) constant) from left to right.

The left boundary is \(x=y^{2}\) (making \(x\) the subject of the equation \(y=\sqrt{x}\)).

The right boundary is \(x=1\) .

These are the limits of integration for \(x\) .

The outer integration is with respect to \(y\). The limits of integration are simply the lower and upper limits of \(y\) for the region of integration.

Lower limit: \(y=0\)

Upper limit: \(y=1\)

Therefore the integral becomes, \(\int_{0}^{1}\left[\int_{x=y^{2}}^{1}(10x-4y+5)\:dx\right]\:dy\)

Thirdly, integrate with respect to \(x\) and then with respect to \(y\).

\[\begin{align*} \int_{0}^{1}\left[\int_{x=y^{2}}^{1}(10x-4y+5)\:dx\right]\:dy & =\int_{0}^{1}\left[\left(5x^{2}-4yx+5x\right)_{x=y^{2}}^{1}\right]\:dy\\ & =\int_{0}^{1}\left[\left(5(1)^{2}-4y(1)+5(1)\right)-\left(5(y^{2})^{2}-4y(y^{2})+5(y^{2})\right)\right]\:dy\\ & =\int_{0}^{1}\left[\left(5-4y+5\right)-\left(5y^{4}-4y^{3}+5y^{2}\right)\right]\:dy\\ & =\int_{0}^{1}\left[-5y^{4}+4y^{3}-5y^{2}-4y+10\right]\:dy\\ & =\left[-y^{5}+y^{4}-\frac{5y^{3}}{3}-2y^{2}+10y\right]_{0}^{1}\\ & =\left(-(1)^{5}+(1)^{4}-\frac{5(1)^{3}}{3}-2(1)^{2}+10(1)\right)-\left(0\right)\\ & =-1+1-\frac{5}{3}-2+10\\ & =\frac{19}{3}\textrm{ or $6\frac{1}{3}.$ } \end{align*}\]

The same answer could be found by reversing the order of integration and evaluating the double integral \(\underset{R}{\iint}(10x-4y+5)\:dy\:dx\).

Example 4: Reversing the Order of Integration in Example 3.

Solution:

Firstly sketch the region of integration.

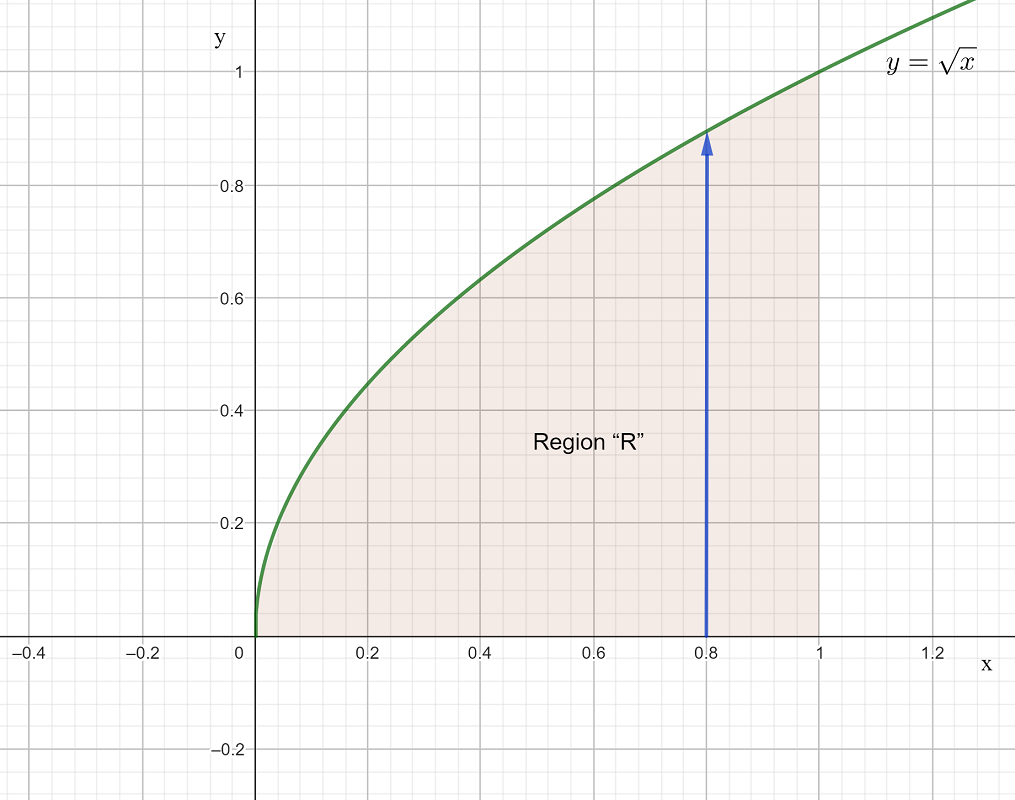
Detail of region if integrating with y first.

Secondly, find the limits of integration.

The “inner” integration is with respect to \(y\) , so we draw an arrow across the region of integration, parallel to the \(y\)-axis (keeping \(x\) constant) from bottom to top.

The lower boundary is \(y=0\)

The upper boundary is \(y=\sqrt{x}\) .

These are the limits of integration for \(y\) .

The outer integration is with respect to \(x\). The limits of integration are simply the left and right limits of \(x\) for the region of integration.

Left limit: \(x=0\)

Right limit: \(x=1\)

Therefore the integral becomes, \(\int_{0}^{1}\left[\int_{0}^{y=\sqrt{x}}(10x-4y+5)\:dy\right]\:dx\)

Thirdly, integrate with respect to \(y\) and then with respect to \(x\).

(You can check this yourself and see that you get the same answer, regardless of the order of integration).

Example 5

Determine the limits of integration for\(\underset{R}{\iint}(2xy)\:dA\) over the region shown below,

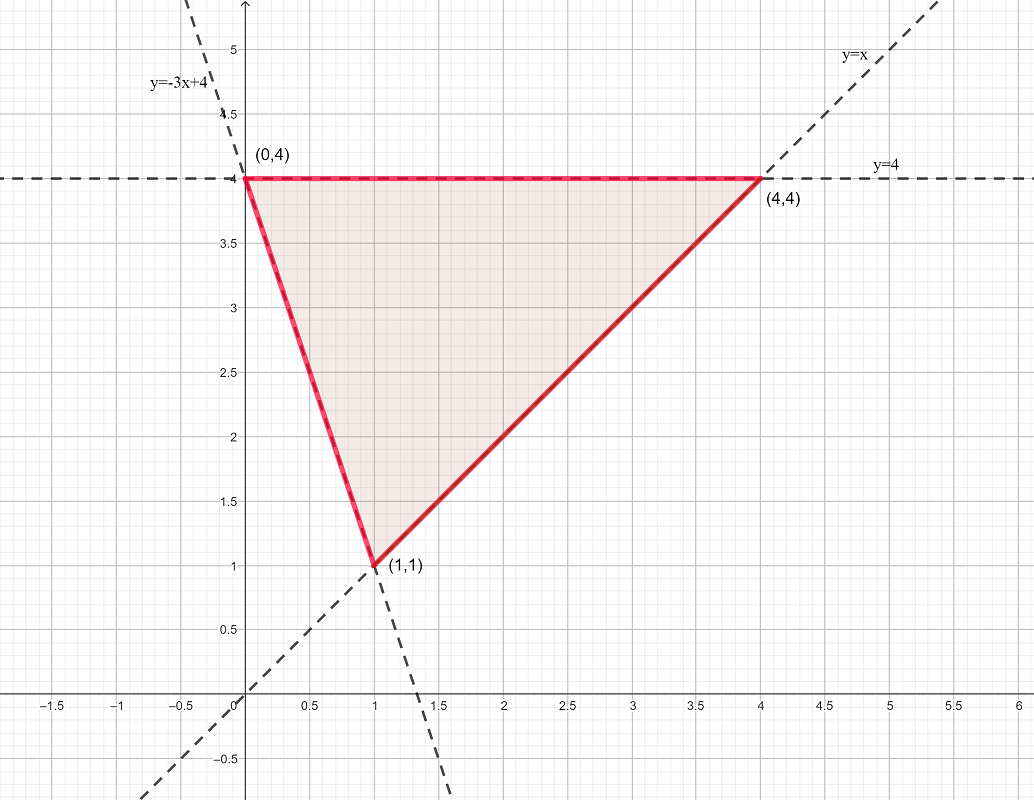
Details of region R

by a) integrating with respect to \(x\) first and b) integrating with respect to \(y\) first.

Solution a) Integrating with respect to \(x\) first.

We draw an arrow parallel to the \(x\)-axis.

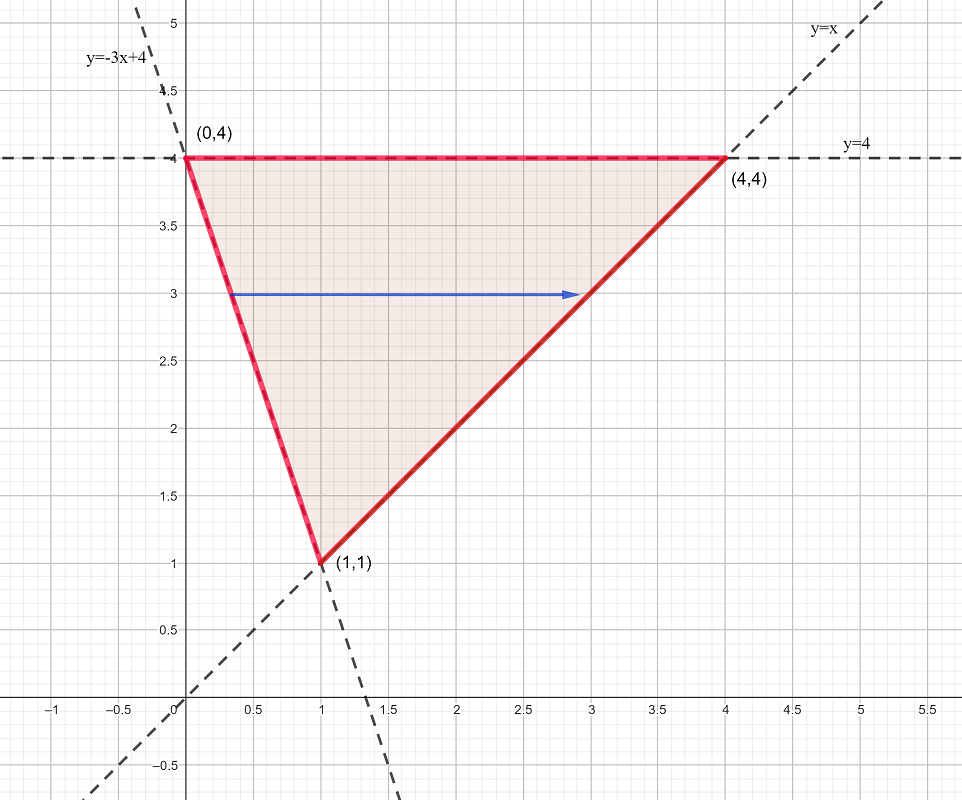
Detail of region R if integrating with x first.

Looking at this arrow, it can be seen that the left limit is \(x=-\frac{1}{3}\left(y-4\right)\) (this is found by re-arranging the equation \(y=-3x+4\)) and the right limit is \(x=y\).

The \(y\)-limits are the lower and upper values of \(y\). Lower limit, \(y=1\) and the upper limit is \(y=4\).

Therefore, the integral becomes \(\int_{1}^{4}\left[\int_{x=-\frac{1}{3}(y-4)}^{x=y}(2xy)\:dx\right]\ dy\)

Solution b) Integrating with respect to \(y\) first.

In this case we need to divide the region in two and draw two lines parallel to the \(y\)-axis.

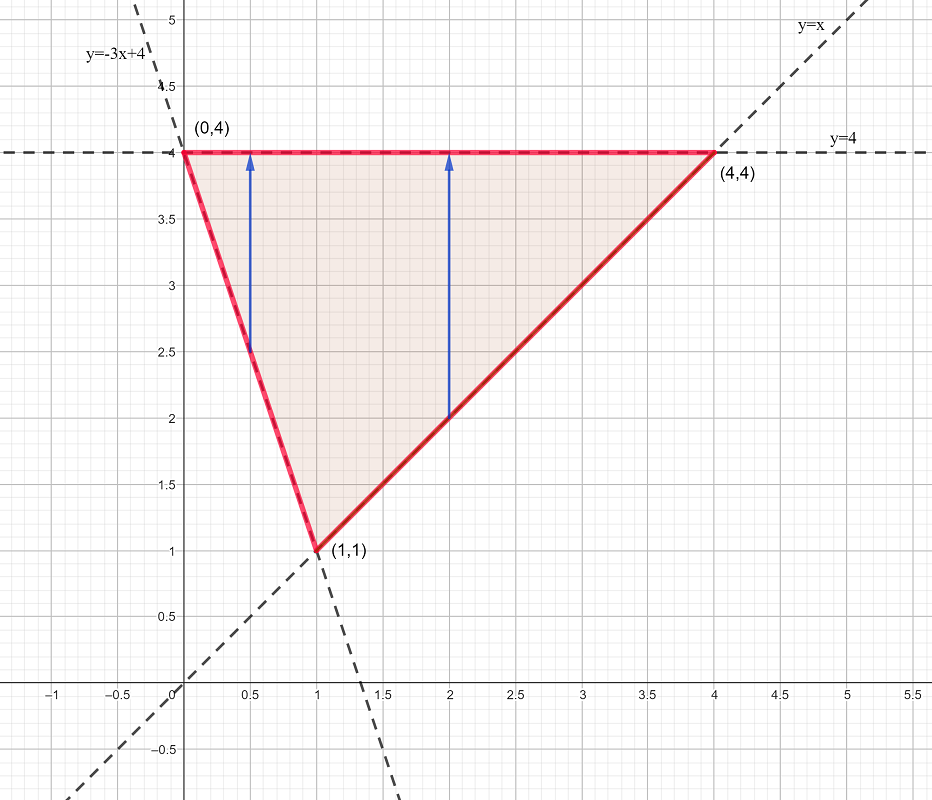
Detailf of region R if integrating with y first.

The diagram shows that, although the upper limit is always \(y=4\), the lower limit changes from \(y=-3x+4\) (between \(x=0\) and \(x=1)\), to \(y=x\) (from \(x=1\) to \(x=4\)).

This gives two double integrals that must be added together to cover the entire region.

\(\int_{0}^{1}\left[\int_{y=-3+4}^{y=4}(2xy)\:dy\right]\ dx+\int_{1}^{4}\left[\int_{y=x}^{y=4}(2xy)\:dy\right]\ dx\)

In this case it appears that integrating with respect to \(x\) first is the easier option.

In fact, sometimes one order may be impossible, but if the order of integration is reversed then the double integral can be evaluated.

Exercise 2

\(\text{a) Evaluate the double integral $\int_{0}^{1}\int_{y=x^{2}}^{y=x}(x^{3}y)\:dy\:dx$ .}\)

\(\text{b})\) Evaluate the double integral \(\int_{0}^{2}\int_{y=x^{2}}^{y=4}(3+2y)\:dy\:dx.\)

\(\text{c) }\)Evaluate the double integral \(\underset{R}{\iint}(4xy)\:dA\) , where \(R\) is the region bounded by the graphs of \(y=x\) and \(y=x^{2}-2x\) .

\(\text{d) }\)Evaluate the double integral \(\underset{R}{\iint}(2x+y)\:dy\:dx\) , where \(R\) is the region bounded by the graphs of \(y+x=2\) and \(y=x^{2}\) .

Answers

\(\text{a) $\frac{1}{48}\quad\quad\text{b) $\frac{208}{5}\text{ or $41\frac{3}{5}\qquad\text{c) $\frac{243}{10}\text{ or $24\frac{3}{10}\qquad\text{d) $\frac{27}{10}$ }$ }$ }$ }$ }$ }\)

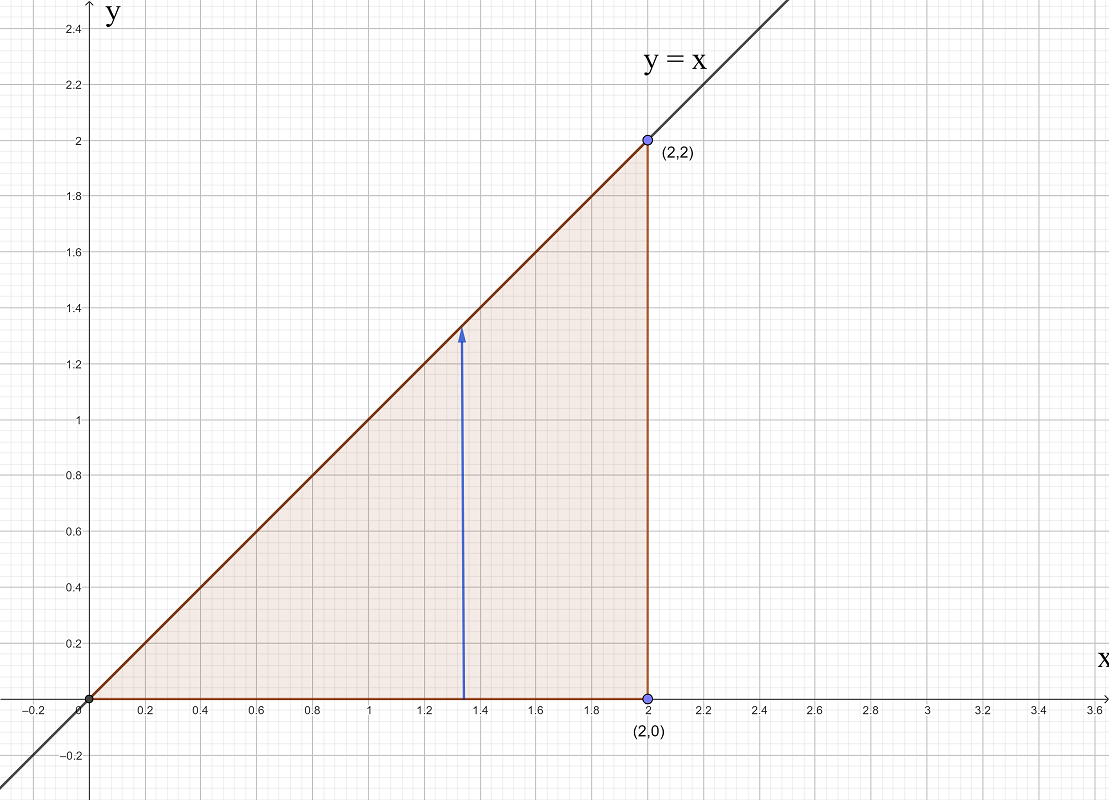
Exercise 3

\(\text{a) }\)Evaluate \(\int_{0}^{2}\left[\int_{y=0}^{y=x}(2x+2y)\:dy\right]\:dx\)

\(\text{b) Sketch the region of integration defined in a).}\)

\(\text{c) Confirm your answer to part a) by evaluating the double integral obtained by reversing the order of integration.}\)

Answers

\(\text{3a) 8}\)

\(\text{3b) }\)

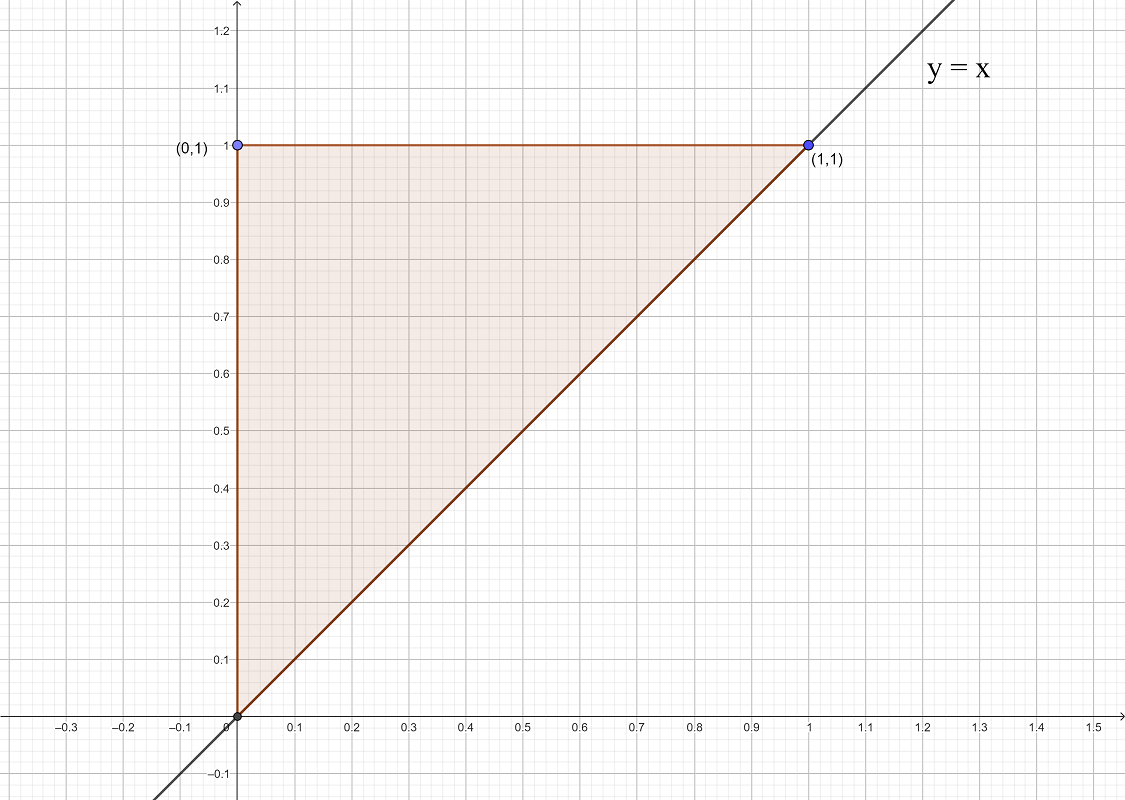
Detail of region R as defined in part a.

Exercise 4

\(\text{a) Sketch the region of integration, R, defined by the double integral $\int_{0}^{1}\left[\int_{y=x}^{y=1}\left(2x\frac{e^{y}}{y^{2}}\right)\:dy\right]\:$ dx }\)

\(\text{b) Reverse the order of integration and hence evaluate.}\)

Answers

\(\text{4a) }\)

Detail of region R.

\(\text{4b) $e-1$ }\)

Download this page, IN9 Double integrals (PDF 1248KB)

Keywords: 
Maths
Integration