D8 Maxima and minima
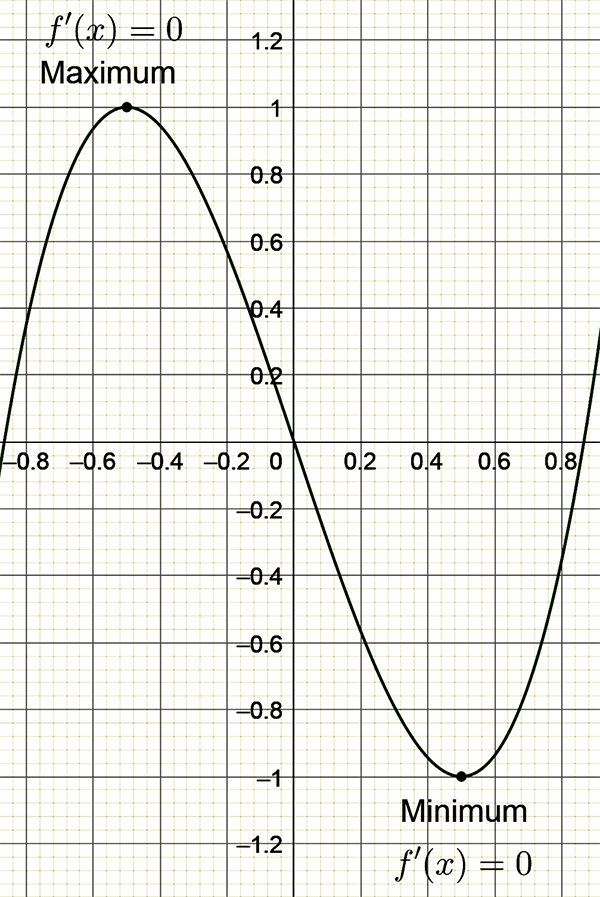
How do you find the maximum (highest) or minimum (lowest) value of a curve? The maximum or minimum values of a function occur where the derivative is zero. That is where the graph of the function has a horizontal tangent.
If you go looking for the horizontal tangents (i.e. where the derivative = 0), you will be able to pinpoint the maxima or minima of a curve.
Using calculus we can find the derivative of a function \(f\left(x\right)\) with respect to \(x\) and use this to find maximum and minimum values of \(f\left(x\right)\) and the values of \(x\) where they occur. We can therefore use calculus to solve problems that involve maximizing or minimizing functions.
Definition
The maximum or minimum values of a function \(f\left(x\right)\) occur when the derivative \[\begin{align*} f'\left(x\right) & =0. & \left(1\right) \end{align*}\]
Second Derivative Test.
Let \(x\) satisfy \(\left(1\right)\) then if \[\begin{align*} f^{"}\left(x\right) & \begin{cases} =0,\text{ $x$ is an inflection point}\\ <0\text{, $f\left(x\right)$ is a local maximum}\\ >0\text{, $f\left(x\right)$ is a local minimum.} \end{cases} \end{align*}\]
Example 1
The distance \(s\,km,\) to the nearest \(km\), of a fishing boat from port at any time, \(t\) hours, is given by the formula \[\begin{align*} s & =2+8t-2.5t^{2}. \end{align*}\] When is the boat furthest from port and what is its distance from the port at that time?
Solution
For a maximum or minimum, \(ds/dt=0.\) That is
\[\begin{align*} \frac{ds}{dt} & =8-5t\\ & =0. \end{align*}\] So, \[\begin{align*} 8-5t & =0\\ 5t & =8\\ t & =1.6\text{ hours.} \end{align*}\] Now this could be a maximum or minimum distance. However, \[\begin{align*} \frac{d^{2}s}{dt^{2}} & =-5\\ & <0. \end{align*}\] Hence \(t=1.6\) is a maximum. When \(t=1.6\) hours, the distance from port, \[\begin{align*} s & =2+8(1.6)-2.5\left(1.6\right)^{2}\\ & =8.4\,km. \end{align*}\] The boat is furthest from port after \(1.6\) hours and the distance from port, at that time, is \(8.4\,km\).
Example 2
Find the maximum product of two numbers that have a sum of \(10.\)
Solution
Let the numbers be \(a\) and \(b\). Then \[\begin{align*} a+b & =10. & \left(2.1\right) \end{align*}\] Let the product of the two numbers be \(P\) so \[\begin{align*} P & =a\times b. \end{align*}\] From \(\left(2.1\right)\)1 We need to get \(P\) in terms of \(a\) or \(b\) so that we take a derivative like \(dP/da\) or \(dP/db\). In this case we write \(P\) as a function of \(b\) but identical results are obtained is we make \(P\) a function of \(a.\) \[\begin{align*} a & =10-b \end{align*}\] so \[\begin{align*} P & =\left(10-b\right)b\\ & =10b-b^{2}. \end{align*}\] Now \[\begin{align*} \frac{dP}{db} & =10-2b. \end{align*}\] For a maximum or minimum, \(dP/db=0,\) \[\begin{align*} 10-2b & =0\\ 2b & =10\\ b & =5. & \left(2.2\right) \end{align*}\] But \[\begin{align*} \frac{d^{2}P}{db^{2}} & =-2\\ & <0 \end{align*}\] and we have a maximum. Substituting \(b=5\) in \(\left(2.1\right)\) we find \(a=5.\)
Hence the two numbers adding to \(10\) and having a maximal product are \(a=b=5\) and the maximum product is \(25.\)
Example 3
Find the minimum value of the function \(f\left(x\right)=x^{2}-5x+6\).
Solution
We have \[\begin{align*} f'\left(x\right) & =2x-5. & \left(3.1\right) \end{align*}\] For a maximum or minimum we know
\[\begin{align*} f'\left(x\right) & =0\\ 2x-5 & =0\\ 2x & =5\\ x & =\frac{5}{2}. \end{align*}\] Since \[\begin{align*} f^{"}\left(x\right) & =2\\ & >0 \end{align*}\] for all values of \(x\) we know we have a minimum. Hence the minimum value of \(f\left(x\right)=x^{2}-5x+6\) occurs at \(5/2.\)
The minimum value of the function is \[\begin{align*} f\left(x\right) & =\left(\frac{5}{2}\right)^{2}-5\left(\frac{5}{2}\right)+6\\ & =\frac{25}{4}-\frac{25}{2}+\frac{12}{2}\\ & =\frac{25}{4}-\frac{50}{4}+\frac{24}{4}\\ & =-\frac{1}{4}. \end{align*}\]
Exercises
Find two positive numbers whose sum is 18 such that the sum of their squares is a minimum.
Find the turning point of the parabola defined by \(y=f(x)=5x^{2}-30x+17\).
What is the maximum area that can be enclosed if a rectangle is created with a piece of wire \(48\,cm\) long?
The annual profit \(P\) made on a garment is related to the number \(n\) that are produced by the formula \(P(n)=300n-7200-0.2n^{2}.\) How many garments should be produced to maximize profit?
The two numbers are both 9.
\(\left(3,-28\right)\)
\(144\textrm{cm}^{2}\)
\(750\)
Download this page, D8 Maxima and minima (PDF 249KB)
What's next... D9 Curve sketching
