D2 Gradients, tangents and derivatives

January 19, 2022 - 11:08am — AJ (e67821)

Open image

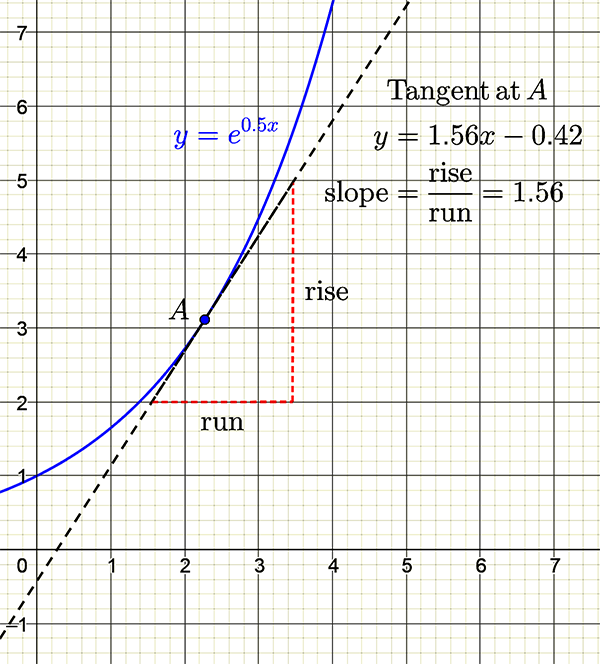
A tangent is a line that touches a curve at only one point. Where that point sits along the function curve, determines the slope (i.e. the gradient) of the tangent to that point.

A derivative of a function gives you the gradient of a tangent at a certain point on a curve. If you plug the x value into the derivative function, you will get the slope of the tangent at that point, defined by the x value. Practice evaluating the gradients of these tangents to a curve.

(See also Functions and graphs)

Gradient of a Curve

In this module we are concerned with finding a formula for the slope or gradient of the tangent at any point on a given curve $y$=$f(x)$.

The formula $m=\frac{y_{2}-y_{1}}{x_{2}-x_{1}}$ may be used to find the gradient of a line when two points on the line, $\left(x_{1},y_{1}\right)$ and $\left(x_{2},y_{2}\right)$ are known.11 There are two special cases that have to be dealt with: horizontal and vertical lines. A horizontal line parallel to the $x$-axis with equation of the form $y=k$ where $k$ is a constant, has a gradient of zero. As a line becomes closer to vertical its gradient gets larger. A vertical line parallel to the $y$-axis with equation of the form $x=c$ where $c$ is a constant has a gradient which is undefined.

Consider the gradient of the curve defined by $y=f(x)$ at the point P (ie the gradient of the tangent line AB).

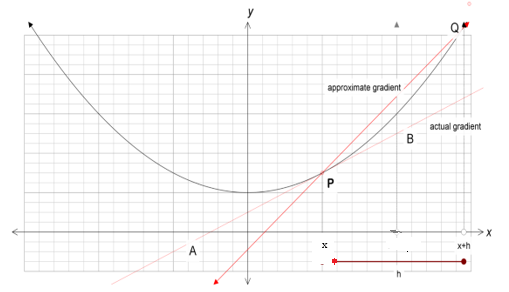
This gradient cannot be calculated as only one point (the point $P$) on the line is known. But the point $P$ has coordinates $\left(x,f(x)\right)$and the point $Q$ has coordinates $\left(x+h,f(x+h)\right)$. The gradient of the line $PQ$ can be calculated and this can be used to approximate the gradient of $AB$. The gradient of $PQ$ = $\frac{f(x+h)-f(x)}{h}$. As the value of $h$ decreases (i.e $Q$ becomes closer to the point $P$), the approximation of the gradient is more accurate. The value of the gradient becomes most accurate as $h$ approaches zero.

The gradient formula for the curve $y=f(x)$ is defined as the derivative function

\[ f'(x)=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h},h\text{$\neq$ }0. \]

The derivative function$f'(x)$ gives the slope of the tangent to the curve$f(x)$ at any point x.

Example

The derivative of the function $f(x)=\frac{3}{x}$ is $f'(x)=-\frac{3}{x^{2}}$. Find the slope of the tangent to the curve at $x=4$.

Solution

At $x$ = 4, \[\begin{align*} f'(x) & =-\frac{3}{4^{2}}\\ & =-\frac{3}{16}. \end{align*}\] Hence the slope of the tangent at $x=4$ is $-\frac{3}{16}\,.$

Exercises

If the derivative function for $f(x)=x^{3}-x$ is $f'(x)=3x^{2}-1$, find the slope of the tangent to this curve at
$\quad\text{a) }x=2\quad\text{b) $x=0\quad\text{c) $x=-9$ .}$ }$

Answer

$\text{a) }11\quad\text{b) $-1\quad\text{c) $x=242\,$ .}$ }$

If the derivative function of $f(x)=\sin\left(x\right)$ is $f'(x)=\cos\left(x\right)$ find the gradient of $f(x)=\sin\left(x\right)$ at
$\quad\text{a) }x=0\quad\text{b) $x=\pi/2\quad\text{c) $x=3.5\,$ .}$ }$

Answer

$\text{a) }1\quad\text{b) $0\quad\text{c) $-0.94$ }$ }$.

Determine $\lim_{h\rightarrow0}\frac{(x+h)^{2}-x^{2}}{h}$ and hence find the slope of the tangent to the curve $y=x^{2}$ at
$\quad\text{a) }x=2\quad\text{b) $x=0\quad\text{c) $x=-9\,$ .}$ }$