D3 Differentiation from first principles
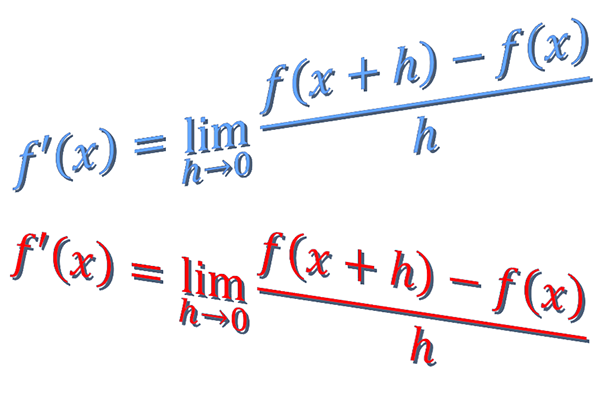
Learn how to take a derivative of a function using first principles. Using this method is the best way to understand the concepts around differentiation.
Start here to really appreciate what you are doing when you differentiate, before you start differentiating using other methods in later modules.
Definition
The derivative of a function \(f\left(x\right)\) is denoted by \(f'\left(x\right)\) and is defined as \[ f'(x)=\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h},h\text{$\neq$ }0. \] Using this definition is called differentiating from first principles.
The result \(f'\left(x\right)\), is called the derivative of \(f\left(x\right)\).
There are rules for differentiation that are far more convenient than using the definition above. In general, you should only use the first principles approach above if you are asked to. This module provides some examples on differentiation from first principles.
Hi, I’m Martin Lindsay from the Study and Learning Centre at RMIT University. This is a short movie on differentiation from first principles.
The process of finding the derivative f-x is equal to the limit as h approaches zero of f, of x plus h, minus f of x, divided by h, is called differentiation from first principles. Just be aware that f-x is the same as dydx.
Let’s look at an example. We want to differentiate f of x as equal to s² minus x from first principles. Notice in the formula that we have three terms to investigate. We have the f of x plus h term, the f of x term, and the h term. So let’s start with the f of x plus h term first. Knowing f of x is equal to x² minus x what we do is we substitute x plus h wherever we see x. In other words, x² becomes x plus h all squared, and x becomes x plus h. So we have x plus h all squared, minus x plus h, which on expansion gives u x² plus 2xh, plus h² minus x minus h.
Now let’s look at the fx term. Well we already know that f of x is equal to s² minus x, so we can simply leave this expression alone. In other words, s² minus x is x² minus x. So, let’s substitute f of x plus h and f of x into the numerator of the formula at the top of the slide, and we get this. Notice on removing the brackets the negative sign at the end of the line two becomes a plus x in line three. Notice also that the x² terms disappear and the h terms cancel out. So we’re left with 2xh plus h² minus h. So let’s now return to the formula and substitute. We have in our numerator 2xh plus h² minus h.
Notice also that the numerator factorises, so we can take h out, giving h brackets 2x plus h minus one. Notice also that there’s an h on the bottom of this fraction, so the h’s cancel, leaving us the bottom line f-x is equal to the limit as h approaches zero of 2x plus h minus one.
Now let’s look at the h approaches zero part of our formula. And what that means is that as h approaches zero, the value of h gets smaller and smaller and smaller. So working your way down the slide notice h gets smaller and smaller and smaller until it approaches zero. So we’re left with f-x is equal to 2x minus one.
So, to conclude, the derivative of fx is equal to a² minus x using first principles is f-x equals 2x minus one.
Now try some questions for yourself. The answers to these questions are on the next slide. Thanks for watching this short movie.
Example 1
If \(f\left(x\right)=x^{2},\) find the derivative of \(f\left(x\right)\) from first principles.
Solution:
Using first principles,1 You need to know the identity \[\begin{align*} \left(a+b\right)^{2} & =a^{2}+2ab+b^{2} \end{align*}\] for this example. In general, you need to know a bit of algebra to do limits effectively.
\[\begin{align*} f'(x) & =\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h},h\text{$\neq$ }0\\ & =\lim_{h\rightarrow0}\frac{(x+h)^{2}-x^{2}}{h}\\ & =\lim_{h\rightarrow0}\frac{x^{2}+2xh+h^{2}-x^{2}}{h}\\ & =\lim_{h\rightarrow0}\frac{2xh+h^{2}}{h}\\ & =\lim_{h\rightarrow0}\frac{h(2x+h)}{h}\\ & =\lim_{h\rightarrow0}2x+h\\ & =2x. \end{align*}\] The derivative of \(x^{2}=2x.\)
Example 2
Determine, from first principles, the gradient function for the curve \(f(x)=2x^{2}-x\) and calculate its value at \(x=3\).
Solution:
Using first principles, \[\begin{align*} f'(x) & =\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h}h\text{$\neq$ }0\\ & =\lim_{h\rightarrow0}\frac{2(x+h)^{2}-(x+h)-(2x^{2}-x)}{h}\\ & =\lim_{h\rightarrow0}\frac{2x^{2}+4xh+2h^{2}-x-h-2x^{2}+x)}{h}\\ & =\lim_{h\rightarrow0}\frac{4xh+2h^{2}-h)}{h}\\ & =\lim_{h\rightarrow0}4x+2h-1\\ & =4x-1. \end{align*}\]
The gradient function is \(f'(x)=4x-1.\) It’s value at \(x=3\) is \[\begin{align*} f'\left(3\right) & =4\left(3\right)-1\\ & =11. \end{align*}\] The value of the gradient function at \(x=3\) is \(11.\)
Example 3
Use differentiation from first principles to find the gradient function of \(y=\frac{1}{x}\).
Solution:
Using first principles,
\[\begin{align*} f'(x) & =\lim_{h\rightarrow0}\frac{f(x+h)-f(x)}{h},h\text{$\neq$ }0\\ & =\lim_{h\rightarrow0}\frac{\frac{1}{x+h}-\frac{1}{x}}{h}\\ & =\lim_{h\rightarrow0}\frac{\frac{x}{x(x+h)}-\frac{x+h}{x(x+h)}}{h}\\ & =\lim_{h\rightarrow0}\frac{\frac{x-(x+h)}{x(x+h)}}{h}\\ & =\lim_{h\rightarrow0}\frac{\frac{-h}{x(x+h)}}{h}\\ & =\lim_{h\rightarrow0}\frac{-1}{x(x+h)}\\ & =\frac{-1}{x^{2}}. \end{align*}\] The gradient function of \(y=\frac{1}{x}\) is \(-\frac{1}{x^{2}}\). In this case we can write \[\begin{align*} \frac{dy}{dx} & =-\frac{1}{x^{2}}. \end{align*}\]
Exercises
Find the derivative of the following functions using differentiation from first principles.
- \(f\left(x\right)=3x.\)
- \(f(x)=5x^{2}\)
- \(f\left(x\right)=2x^{2}-1/x\)
1. \[\begin{align*} f'\left(x\right) & =\lim_{h\rightarrow0}\frac{3(x+h)-3x}{h}\\ & =\lim_{h\rightarrow0}\frac{3x+3h-3x}{h}\\ & =\lim_{h\rightarrow0}\frac{3h}{h}\\ & =\lim_{h\rightarrow0}\frac{3}{1}\\ & =3. \end{align*}\]
2. \[\begin{align*} f'\left(x\right) & =\lim_{h\rightarrow0}\frac{5(x+h)^{2}-5x^{2}}{h}\\ & =\lim_{h\rightarrow0}\frac{5(x^{2}+2xh+h^{2})-5x^{2}}{h}\\ & =\lim_{h\rightarrow0}\frac{5x^{2}+10xh+5h^{2}-5x^{2}}{h}\\ & =\lim_{h\rightarrow0}\frac{10xh+5h^{2}}{h}\\ & =\lim_{h\rightarrow0}10x+5h\\ & =10x. \end{align*}\]
3.\[\begin{align*} f'\left(x\right) & =\lim_{h\rightarrow0}\frac{2\left(x+h\right)^{2}-\frac{1}{x+h}-\left(2x^{2}-\frac{1}{x}\right)}{h}\\ & =\lim_{h\rightarrow0}\frac{2\left(x^{2}+2xh+h^{2}\right)-\frac{1}{x+h}-\left(2x^{2}-1/x\right)}{h}\\ & =\lim_{h\rightarrow0}\frac{2x^{2}+4xh+2h^{2}-\frac{1}{x+h}-\left(2x^{2}-1/x\right)}{h}\\ & =\lim_{h\rightarrow0}\frac{4xh+2h^{2}-\frac{1}{x+h}+\frac{1}{x}}{h}\\ & =\lim_{h\rightarrow0}\frac{4xh+2h^{2}-\frac{x}{x\left(x+h\right)}+\frac{x+h}{x\left(x+h\right)}}{h}\\ & =\lim_{h\rightarrow0}\frac{4xh+2h^{2}+\frac{h}{x\left(x+h\right)}}{h}\\ & =\lim_{h\rightarrow0}4x+2h+\frac{1}{x\left(x+h\right)}\\ & =4x+\frac{1}{x^{2}}. \end{align*}\]
Download this page, D3 Differentiation from first principles (PDF 241KB)
What's next... D4 Rules for differentiation
