D10 Rates of change
 Image: Pixabay
Image: Pixabay
If there is a relationship between two or more variables (like, area and radius of a circle (A = πr2 ), or pressure, volume and temperature of a gas), then there will also be a relationship between how these variables change. You may need to find how fast one variable changes in relation to another variable that is changing. This is called the rate of change.
If there is a relationship between two or more variables, for example, area and radius of a circle (\(A\)=\(\pi r^{2}\)), or length of a side and volume of a cube (\(V=l^{3}\)), or days since first case and number of people with an infectious disease then there will also be a relationship between the rates at which the variables change. If \(y\) is a function of \(x\), that is \(y=f(x)\), then \(\frac{dy}{dx}=f'\left(x\right)\).
We can use differentiation to find the function that defines the rate of change between variables
\[\begin{align*} A=\pi r^{2}\Rightarrow\frac{dA}{dr} & =2\pi r\\ \textrm{and }V=l^{3}\Rightarrow\frac{dV}{dl} & =3l^{2} \end{align*}\]
The chain rule can be used to find rates of change with respect to time:
\[ \frac{dy}{dt}=\frac{dy}{dx}\times\frac{dx}{dt} \]
\[\begin{align*} A=\pi r^{2}\Rightarrow\frac{dA}{dt} & =\frac{dA}{dr}\times\frac{dr}{dt}\\ \frac{dA}{dt} & =2\pi r\frac{dr}{dt} \end{align*}\]
\[\begin{align*} \textrm{and }V=l^{3}\Rightarrow\frac{dV}{dt} & =\frac{dV}{dl}\times\frac{dl}{dt}\\ \frac{dV}{dt} & =3l^{2}\frac{dl}{dt} \end{align*}\]
Examples
A balloon has a small hole and its volume \(V\) in cubic centimeters after \(t\) seconds is \(V=66-10t-0.01t^{2}\), \(t>0\). Find the rate of change of volume after 10 seconds. \[\begin{align*} V & =66-10t-0.01t^{2}\\ \frac{dV}{dt} & =-10-0.02t\\ \textrm{When $t=10,$ $\frac{dV}{dt}$ } & =-10-0.02\left(10\right)\\ & =-10.2\,cm^{3}/s. \end{align*}\] The volume of the balloon is decreasing at a rate of \(10.2cm^{3}/s.\)
The pressure \(P\), of a given mass of gas kept at constant temperature, and its volume \(V\) are connected by the equation \(PV\) = 500. Find \(\frac{dP}{dV}\) when \(V\) = 20. \[\begin{align*} PV=500\Rightarrow P & =\frac{500}{V}\\ P & =500V^{-1}\\ \textrm{Then }\frac{dP}{dV} & =-500V^{-2}\\ V=20\Rightarrow\frac{dP}{dV} & =-500(20)^{-2}\\ & =-1.25. \end{align*}\] The rate of change of pressure with respect to volume is \(-1.25.\)
A ladder 4.5m long ladder is sliding down a vertical wall with the top descending at a rate of \(2.3\,m/s.\) How fast is the bottom of the ladder moving along the ground when the bottom is 3 meters from the wall?
A diagram reveals that the information in the question is described by Pythagoras’s theorem:1 Pythagoras’s theorem: \(a^{2}+b^{2}=c^{2}\) where \(c\) is the hypotenuse and \(a\) and \(b\) the shorter sides of a right triangle.
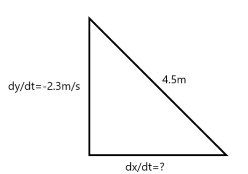
If \(y\) is the height the ladder reaches up the wall and \(x\) is the distance of the bottom of the ladder from the wall then \[\begin{align*} x^{2}+y^{2} & =4.5^{2}\\ 2x\frac{dx}{dt}+2y\frac{dy}{dt} & =0\ \ [\textrm{differentiating implicitly]}\\ 2\times3\times\frac{dx}{dt}+2\times3.35\times(-2.3 & )=0\ \ [a=3,c=4.5\Rightarrow b=3.35]\\ 6\frac{dx}{dt}-15.41 & =0\\ \Rightarrow\frac{dx}{dt} & =2.57 \end{align*}\] The ladder is moving along the ground at a speed of \(2.57\,m/s\).
Exercise
The radius of a spherical balloon is increasing at a rate of 3cm/min. At what rate is the volume increasing when the radius is 5cm?
Answer: \(300\pi\approx942cm^{3}/min\)If the displacement of an object from a starting point is given by \(s(t)=\sin\left(t\right)-2\cos\left(t\right)\) find the velocity when \(t=1\). Hint: \(v(t)=s'(t)=\frac{ds}{dt}\)
Answer: \(2.22\)The function \(n(t)=200t-100\sqrt{t}\) describes the spread of a virus where \(t\) is the number of days since the initial infection and \(n\) is the number of people infected. Find the rate at which \(n\) is increasing at the instant when \(t=4\).
Answer: \(175\) people per day.If \(y=(x-\frac{1}{x})^{2}\) find \(\frac{dx}{dt}\) when \(x=2\), given \(\frac{dy}{dt}\) = 1.
Answer:4/15A hollow right circular cone is held vertex downwards beneath a tap leaking at the rate of \(2\,cm^{3}/s\). Find the rate of rise of water level when the depth is \(6\,cm\) given that the height of the cone is \(18\,cm\) and its radius is \(12\,cm\). (Hint: Use the properties of similar triangles to find a relationship between radius and height.)
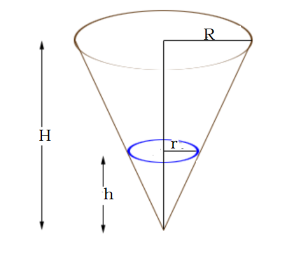
Answer: \(\frac{1}{8\pi}\,cm/s\approx0.04\,cm/s\)
Download this page, D10 Rates of Change (PDF 554KB)
What's next... D11 Small changes and approximations
