D1 Limit of a function
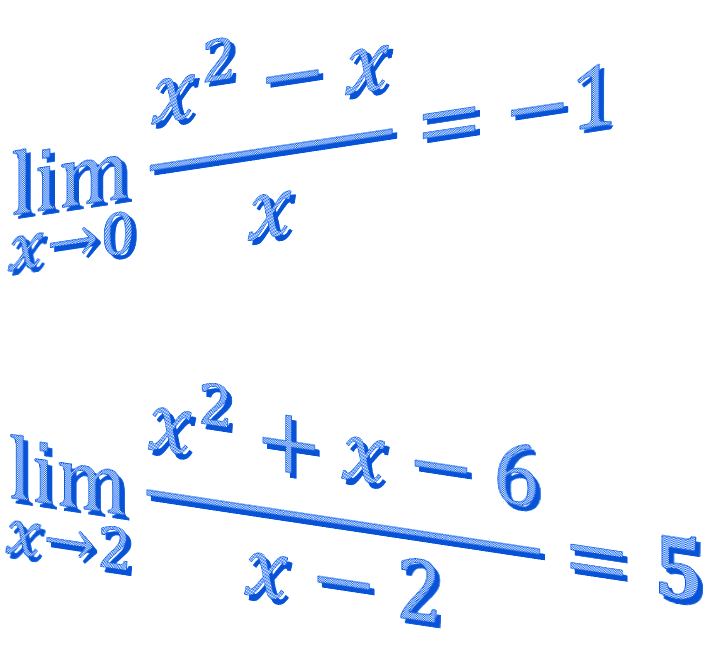
The limit of a function means finding the value of a curve at a particular point. But what is that point? A value to many decimal places can be very long, to define a value that is very precise. The precise point can be infinitely small.
We can only ask what the value of the curve is as we get closer to that point, from values above and from values below. That is what we mean by approaching the limit.
This short maths video demonstrates the limit of a function which describes the behaviour of this function in the vicinity of a particular value of the variable, which is usually x.
Hi, I’m Martin Lindsay from the Study and Learning Centre at RMIT University. This is another movie on differentiation. This time we’re focusing on limits.
The limit of a function by definition describes the behaviour of this function in the vicinity of a particular value of the variable, which is usually x. Let’s look at the function x2 plus one, and investigate the limit of this function as it approaches x equals one. Let’s first sketch the function fx equals x2 plus one. As you can see, it’s a parabler, y equals x2, which has been shifted up the y axis one unit. Point of interest here is the point at x equals one and y equals two, and we will refer back to this slide a little later.
What we do first of all is to find values of x as it approaches one from below. In other words, we’re moving from the left-hand side of the graph up to the value of x equals one. Go back to the previous slide. If we do that as x approaches one from the left or below the values of the function will approach two. In other words, as x approaches one from below, x2 plus one approaches two.
Now let’s investigate what happens to x as it approaches one from above. In other words, we’re moving from the right of the graph to the value of x equals one. Go back to the slide again to see the red arrows indicating this. When we plug in our values of x as they approach one from the right or above, the values of fx approach as you can see, two. So as x approaches one from above, x2 plus one approaches two.
So in both cases, below one and above one, as x approaches one the value of x2 plus one approaches two. So we say more formally that the limit of x2 plus one as x approaches one is equal to two.
Now let’s investigate the limit of a more complicated function. Here the function fx is equal to x2minus one divided by x minus one, again as it approaches x equals one. Let’s investigate this function more closely. Notice that if we let x equals one, the denominator of this function will be zero. In other words, it’s not defined at x equals one. We say it is not continuous at x equals one. If we restrict our function to all values except for x is equal to one, we can now progress and factorise this function, x2 minus x becomes x brackets x minus one. Notice that we can cancel terms top and bottom. In other words, the function fx is equal to x.
So sketching the function fx equals x as you would expect, we have a straight line for all values except for x equals one, and this is the point at which we will be investigating the limit. In other words, f of one does not exist, but as x approaches one, the value of f of x approaches one as well. So more formally since f of x if equal to x, then the limit of x2 minus x over x minus one as x approaches one is equal to one.
Now try some questions for yourself. The answers to these questions are on the next slide. Thanks for watching this short movie.
Definition
If the value of the function as we approach a particular value \(x=a\) is the same whether we are approaching from the left or the right then the limit exists. The function need not be continuous or even defined at the point of interest. For the function below, the limit of \(f(x)\) as \(x\) approaches \(2\) is \(4\).
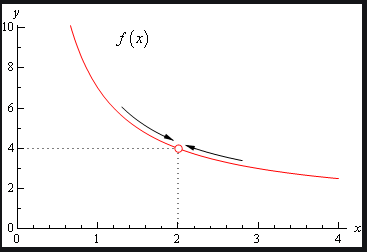
We say, \[ \lim_{x\rightarrow2}f(x)=4. \]
Examples
- Find the limit of the function \(f(x)=x+2\) as \(x\) approaches \(2.\)
Solution:
The behaviour of \(f(x)\) as \(x\) \(\rightarrow\) 2 is shown in the table:
| \(x\) | 1.95 | 1.995 | \(\dashrightarrow\) 2 \(\dashleftarrow\) | 2.005 | 2.05 |
|---|---|---|---|---|---|
| \(f(x)\) | 3.95 | 3.995 | \(\dashrightarrow\) 4 \(\dashleftarrow\) | 4.005 | 4.05 |
The table shows that as \(x\) approaches 2, \(f(x)\) approaches 4
Alternatively, because this function is defined at \(x=2,\) we could substitute \(x=2\) into the function:
\[ f(2)=2+2=4 \]
Therefore \[ \lim_{x\rightarrow2}\left(x+2\right)=4. \]
- Find \(\lim_{h\rightarrow0}\)(\(5x^{2}+2xh+h\)) .
Solution:
The 2\(xh\) and \(h\) terms will approach zero as \(h\) approaches zero. The limit can be found by substituting zero for \(h\):
\[\begin{align*} \lim_{h\rightarrow0}(5x^{2}+2xh+h) & =5x^{2}+2\times0+0\\ & =5x^{2} \end{align*}\]
- Find \(\lim_{x\rightarrow1}\) \(\tfrac{x^{2}-1}{x-1}\).
Solution: It is not possible to find the limit by substituting \(x=1\) as we would then have \(0\) in the denominator. We can find this limit, if we simplify the expression first and then substitute.1 You need to know the difference of two squares, \[ a^{2}-b^{2}=\left(a-b\right)\left(a+b\right). \] Applying this gives: \[ x^{2}-1=\left(x-1\right)\left(x+1\right). \]
In this case \[\begin{align*} \lim_{x\rightarrow1}\tfrac{x^{2}-1}{x-1} & =\lim_{x\rightarrow1}\tfrac{(x-1)(x+1)}{x-1}\\ & =\lim_{x\rightarrow1}x+1\\ & =2. \end{align*}\]
- Find \(\lim_{h\rightarrow0}\sin\left(h\right)/h\).
Solution:
It is not possible to find the limit by substituting \(h=0\). But consider the behaviour of \(f(h)=\frac{\sin(h)}{h}\) as \(h\rightarrow0\):
| \(h\) | -0.5 | -0.3 | -0.2 | -0.1 | 0 | 0.01 | 0.1 | 0.2 | 0.3 | 0.5 |
|---|---|---|---|---|---|---|---|---|---|---|
| \(f(h)\) | 0.959 | 0.985 | 0.993 | 0.998 | ? | 0.99998 | 0.998 | 0.993 | 0.985 | 0.959 |
It appears that \[ \lim_{h\rightarrow0}\frac{\sin(h)}{h}=1. \]
Exercises
Determine the following limits:
\(1)\lim_{x\rightarrow0}\left(4xh+2\right)\)
\(2)\lim_{x\rightarrow0}\frac{9-x^{2}}{4}\)
\(3)\lim_{h\rightarrow0}\frac{xh-2h}{h}\)
\(4)\lim_{x\rightarrow0}\frac{\tan(x)}{x}\)
2
9/4
x – 2
1
Download this page, D1 Limits (PDF 208KB)
What's next... D2 Gradients, tangents and derivatives
