D6 The product rule
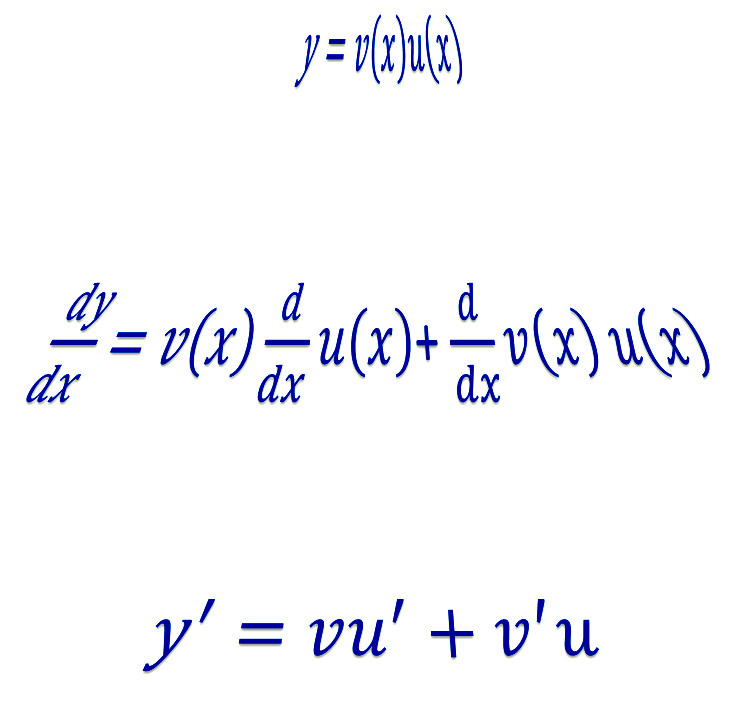
What is the product rule? It is useful when you want to differentiate a function that comprises one function multiplied by another function.
The derivatives of functions such as \(y=f(x)=2x\sin\left(x\right)\) and \(y=f(x)=xe^{x}\) can be found using the product rule.
Definition
If \[\begin{align*} y & =f\left(x\right)\\ & =u\left(x\right)\cdot v\left(x\right) \end{align*}\] then \[\begin{align*} y' & =f'\left(x\right)\\ & =u\left(x\right)\cdot v'\left(x\right)+u'\left(x\right)\cdot v\left(x\right). \end{align*}\] This is often abbreviated to \[\begin{align*} y' & =uv'+u'v. \end{align*}\]
Hi, I’m Martin Lindsay from the Study and Learning Centre at RMIT University. This is a short movie on the product rule.
The product rule is used when we want to differentiate the product of two functions. So, if f of x, is equal to u of x times v of x, then the derivative f dash x is u of x times v dash x plus u dash x times vx. This formula can be abbreviated to y dash is equal to u times v dash, plus v times u dash. Note also that f dash x and y dash mean the same thing. So lets do a couple of examples to illustrate the product rule. Here’s a function, x plus 3 to the power of six multiplied by 2x minus 1. Notice here that there are two functions so we can use the product rule. So, let u equal x plus 3 to the power of 6, therefore the derivative is u dash equals 6 brackets x plus 3 to the power of five and let v equals 2x minus 1, and the derivative there is v dash equals 2. Notice I’ve used the chain rule to work out u dash. Substituting in to the formula y dash equals uv dash plus vu dash I get the following four lines of working. Notice when you get down to the third line that I’ve taken a factor of 2 brackets x plus 3 to the power of 5 out, and in the last line I’ve simplified the expression inside the square brackets to give us an answer of 14x brackets x plus 3 all to the power of 5.
Here’s another example. Again notice that there are two functions here e to the x multiplied by sin of 2x. So, this lends itself to the product rule. So I’m letting u equals e to the x, the derivative is the same e to the x and v equals sin of 2 x from which the derivative is 2 cos of 2 x using the chain rule. Substituting as before into the formula y dash equals uv dash plus vu dash I get the following three lines of working. Notice again always look for terms that will factorise and I’ve done that in the last line. So my answer is y dash is equal to ex brackets 2 cos 2x plus sin of 2 x.
Now try some questions for yourself. The answers to these questions are on the next slide. Thanks for watching this short movie.
Examples
- Find the derivative of \(f(x)=\left(x+3\right)^{6}\left(2x-1\right).\)
Solution:
Let \(u=(x+3)^{6}\) and \(v=2x-1,\) then using the chain rule1 Let \(w=x+3\) then \(u=w^{6}\) and \[\begin{align*} u' & =\frac{du}{dw}\times\frac{dw}{dx}\\ & =6w^{5}\cdot1\\ & =6\left(x+3\right)^{5}. \end{align*}\] \[\begin{align*} u' & =6(x+3)^{5} \end{align*}\] and \[\begin{align*} v' & =2. \end{align*}\] Hence, using the product rule,
\[\begin{align*} \textrm{}y' & =uv'+u'v\\ & =\left(x+3\right)^{6}\cdot2+6\left(x+3\right){}^{5}\left(2x\text{\textendash}1\right)\\ & =(x+3)^{5}\left[2\left(x+3\right)+6\left(2x-1\right)\right]\\ & =14x(x+3)^{5}. \end{align*}\]
- Differentiate \(e^{x}\sin\left(2x\right).\)
Solution:
Let \(u=e^{x}\) and \(v=\sin\left(2x\right),\) then \[\begin{align*} u' & =e^{x}\\ v' & =2\cos\left(2x\right) \end{align*}\] where we have used the chain rule to evaluate \(v'.\)2 Let \(w=2x\) then \(v=\sin\left(w\right)\) and \[\begin{align*} v' & =\frac{dv}{dw}\times\frac{dw}{dx}\\ & =\cos\left(w\right)\cdot2\\ & =2\cos\left(2x\right). \end{align*}\] Hence, using the product rule,
\[\begin{align*} y' & =uv'+u'v\\ & =e^{x}\cdot2\cos\left(2x\right)+e^{x}\sin\left(2x\right)\\ & =2e^{x}\cos\left(2x\right)+e^{x}\sin\left(2x\right)\\ & =e^{x}\left(2\cos\left(2x\right)+\sin\left(2x\right)\right). \end{align*}\]
Exercises
- Use the product rule to differentiate the following
\(\text{$\qquad$ a) }\) \(y\) \(=\left(x-2\right)\left(6x+7\right)\textrm{ and}\) simplify as far as possible.
\(\text{$\qquad$ b) }\) \(f(x)=\left(2x^{2}+4\right)\left(x^{5}+4x^{2}-2\right)\) (do not simplify).
\(\text{$\qquad$ c) }\) \(y=\left(\sqrt{x}-1\right)\left(x^{2}+1\right)\)
\(\text{$\qquad$ d) }\) \(y=\left(x^{3}-4x+\sqrt{x}\right)\left(3x^{4}+2\right).\)
(Note that answers may be written differently)
\(\text{$\qquad$ a) }\) \(12x-5\)
\(\text{$\qquad$ b) }\) \(\left(2x^{2}+4\right)\left(5x^{4}+8x\right)+4x\left(x^{5}+4x^{2}-2\right)\)
\(\text{$\qquad$ c) }\) \(\frac{5}{2}x^{3/2}-2x+\frac{1}{2\sqrt{x}}\)
\(\text{$\qquad$ d) }\) \(12x^{3}\left(x^{3}-4x+\sqrt{x}\right)+\left(3x^{4}+2\right)\left(3x^{2}-4+\frac{1}{2\sqrt{x}}\right)\)
- Find the derivative of
\(\qquad\text{a)}\) \(y=e^{x}\tan x\)
\(\qquad\text{b)}\) \(y=x^{2}\log_{e}x\)
\(\qquad\text{c)}\) \(y=\sin x\cos x\)
\(\qquad\text{d)}\) \(y=\frac{e^{x}}{x}\) \(\textrm{Hint}:\frac{1}{x}=x^{-1}.\)
(Note that answers may be written differently)
\(\qquad\text{a)}\) \(e^{x}\tan x+e^{x}\sec^{2}x\)
\(\qquad\text{b)}\) \(x+2x\log_{e}x\)
\(\qquad\text{c)}\) \(\cos^{2}\left(x\right)-\sin^{2}\left(x\right)\)
\(\qquad\text{d)}\) \(\frac{e^{x}}{x}-\frac{e^{x}}{x^{2}}=e^{x}\left(\frac{1}{x}-\frac{1}{x^{2}}\right)\)
Download this page, D6 The product rule (PDF 153KB)
What's next... D7 The quotient rule
