D13 Partial differentiation
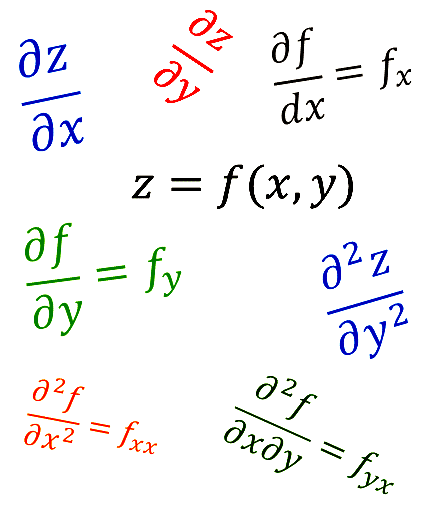
Partial derivatives reveal how a function with many variables changes when you adjust just one of the variables in the input.
Let us suppose that we have the equation for a paraboloid with an elliptical cross-section such as \(z=x^{2}+4y^{2}.\) In this case we have a function of two independent variables, \(z=f\left(x,y\right),\) and its graph is a 3-dimensional surface. We need to be able to differentiate \(z\) with respect to either \(x\) or \(y\). If we treat one of the variables, say \(y\), as a constant, then we can treat \(z\) as a function of just one variable, \(x\). We can then calculate the derivative of \(z\) with respect to \(x\). This derivative is called the partial derivative of \(z\) with respect to \(x\) and is denoted by \(\frac{\partial z }{\partial x}\). If we treat \(x\) as a constant then we can treat \(z\) as a function of \(y\) and we can then calculate \(\frac{\partial z }{\partial y}\) the partial derivative of \(z\) with respect to \(y\).
Examples
- If \(z=x^{2}+4y^{2}\) find \(\frac{\partial z }{\partial x}\) and \(\frac{\partial z }{\partial y}\)
\[\begin{align*} \frac{\partial z }{\partial x} & =2x+0\quad[\textrm{since $y$ is treated as a constant}]\\ & =2x\\ \frac{\partial z }{\partial y} & =0+8y\quad[\textrm{since $x$ is treated as a constant}]\\ & =8y. \end{align*}\]
If \(f(x,y)=xy+2y^{2}\) find \(\frac{\partial f }{\partial x}\) and \(\frac{\partial f }{\partial y}\) \[\begin{align*} \frac{\partial f }{\partial x} & =y+0\quad[\text{Just as the derivative of $2x\text{ is $x,$ the derivative of $xy\text{ is $y\text{ }$ }$ }$ }\\ & \quad\quad\quad\quad\quad\text{when $y\text{ is treated as a constant]}$ }\\ & =y\\ \frac{\partial f }{\partial y} & =x+4y \end{align*}\]
If \(f(x,y)=x^{2}y+y^{2}\sin x\) find \(\frac{\partial f }{\partial x}\) and \(\frac{\partial f }{\partial y}\) \[\begin{align*} \frac{\partial f }{\partial x} & =2xy+y^{2}\cos x\\ \frac{\partial f }{\partial y} & =x^{2}+2y\sin x \end{align*}\]
If \(f(x,y)=xy^{2}\sin(xy)\) find \(\frac{\partial f }{\partial x}\) and \(\frac{\partial f }{\partial y}\) \[\begin{align*} \frac{\partial f }{\partial x} & =y^{2}\sin(xy)+xy^{2}\times y\cos(xy)[\textrm{applying the product rule}]\\ & =y^{2}\sin(xy)+xy^{3}\cos(xy)\\ \frac{\partial f }{\partial y} & =2xy\sin(xy)+xy^{2}\times x\cos(xy)\\ & =2xy\sin(xy)+x^{2}y^{2}\cos(xy) \end{align*}\]
Alternative Notation and Evaluation at a Point
An alternative notation for partial derivatives is \(f_{x}\) for \(\frac{\partial f }{\partial x}\)and \(f_{y}\) for \(\frac{\partial f }{\partial y}\).
Partial derivatives may be evaluated at particular points: \(f_{x}(2,1)\) refers to the value of the partial derivative of \(f\) with respect to \(x\) at the point where \(x=2\) and \(y=1\).
Example
If \(f(x,y)=2x^{3}y+3y^{2}\) find \(f_{y}(1,3)\)
\[\begin{align*} f(x,y) & =2x^{3}y+3y^{2}\\ \Rightarrow f_{y} & =2x^{3}+6y\\ \Rightarrow f_{y}(1,3) & =2+18\\ & =20. \end{align*}\]
Higher Order Partial Derivatives
As we have seen, a function \(z\)= \(f(x,y)\) has two partial derivatives. They are \(\frac{\partial f }{\partial x}\) and \(\frac{\partial f }{\partial y}.\)
A function such as this will have four second order partial derivatives:
It can be differentiated with respect to \(x\) and then with respect to \(x\) again \(\frac{\partial }{\partial x}\left(\frac{\partial f }{\partial x}\right)\)=\(\frac{\partial ^2 f }{\partial x^{2}}=\) \(f_{xx}\)
It can be differentiated with respect to \(y\) and then with respect to \(y\) again\(\frac{\partial }{\partial y}\left(\frac{\partial f }{\partial y}\right)\)=\(\frac{\partial ^ {2} f }{\partial y^2}=\) \(f_{yy}\)
It can be differentiated with respect to \(x\) and then with respect to \(y\) \(\frac{\partial }{\partial y }\left(\frac{\partial f }{\partial x}\right)\)=\(\frac{\partial ^2 f }{\partial x\partial y}=\) \(f_{xy}\)
It can be differentiated with respect to \(y\) and then with respect to \(x\) \(\frac{\partial }{\partial x}\left(\frac{\partial f }{\partial y}\right)\)=\(\frac{\partial ^2 f }{\partial y\partial x}=\) \(f_{yx}\)
Example
Find all second order partial derivatives of \(f(x,y)=x^{2}y^{3}+2x\cos y\)
\[\begin{align*} f_{x} & =2xy^{3}+2\cos y\\ \Rightarrow f_{xx}=2y^{3} & \textrm{and }f_{xy}=6xy^{2}-2\sin y\\ f_{y} & =3x^{2}y-2x\cos y\\ \Rightarrow f_{yy}=6x^{2}y-2x\sin y & \textrm{and $f_{yx}$ }=6xy^{2}-2\sin y \end{align*}\]
(Note that \(f_{xy}=f_{yx}.\) This will always be the case.)
Exercises
\(1.\) Find the partial derivatives \(\frac{\partial z }{\partial x}\) and \(\frac{\partial z }{\partial y}\)for each of the following
\(\quad\text{a) $z=3x^{4}+2y^{3}$ }\)
\(\quad\)b) \(z=x^{2}y\)
\(\quad\text{c)}\) \(z=3xe^{2y}\)
\(\quad\text{d)}\) \(z\) = \(\ln(x^{3}y^{5}-2)\)
\(\quad\text{a) $\frac{\partial z }{\partial x}=12x^{3},$ $\frac{\partial z }{\partial y}$ =6$y^{2}$ }\)
\(\quad\)b) \(\frac{\partial z }{\partial x}=2xy\), \(\frac{\partial z }{\partial y}=x^{2}\)
\(\quad\text{c)}\) \(\frac{\partial z }{\partial x}=3e^{2y},\frac{\partial z }{\partial y}=6xe^{2y}\)
\(\quad\text{d)}\) \(\frac{\partial z }{\partial x}\)=\(\frac{3x^{2}y^{5}}{x^{3}y^{5}-2},\) \(\frac{\partial z }{\partial y}=\frac{5x^{3}y^{4}}{x^{3}y^{5}-2}\)
\(2.\) Find the value of the indicated partial derivative at the given point
\(\text{$\quad$ a)}\) \(f(x,y)=x^{4}-4y^{2},\text{ find }f_{x}(2,3)\)
\(\text{$\quad$ b})\) \(f(x,y)=\ln(x^{2}+y^{3})\text{, find }f_{y}(-1,1)\)
\(\text{$\quad$ a)}\) 32
\(\text{$\quad$ b})\) 1.5
\(3.\) Find the first and second order partial derivatives of the following
\(\quad\text{a)}\) \(f(x,y)=x\ln(y)\)
\(\quad\text{b)}\) \(f(x,y)=x^{3}+x^{2}y-3xy^{2}+y^{3}\)
\(\quad\text{c)}\) \(f(x,y)=\sin(xy)\)
\(\quad\text{d)}\) \(f(x,y)=x\cos y+ye^{x}\)
\(\quad\text{a)}\) \(f_{x}=\ln y,\) \(f_{y}=\frac{x}{y}\), \(f_{xx}=0,f_{xy}=-\frac{x}{y^{2}}\),\(f_{xy}=f_{yx}=\frac{1}{y}\)
\(\quad\text{b)}\) \(f_{x}=3x^{2}+2xy-3y^{2},\) \(f_{y}=x^{2}-6xy+3y^{2},\)
\(\qquad\ f_{xx}=6x+6y,f_{yy}=-6x+6y,f_{xy}=f_{yx}=2x-6y\)
\(\quad\text{c)}\) \(f_{x}=y\cos(xy),\,f_{y}=x\cos(xy),\,f_{xx}=-y^{2}\sin(xy),\)
\(\quad\!\quad\) \(f_{yy}=-x^{2}\sin(xy),\,f_{xy}=f_{yx}=-xy\sin(xy)+\cos(xy)\)
\(\quad\text{d)}\) \(f_{x}=\cos y+ye^{x},\) \(f_{y}=x\sin y+e^{x},\) \(f_{xx}=ye^{x},\)
\(\quad\quad\!\ f_{yy}=-x\cos y,f_{xy}=f_{yx}=e^{x}-\sin y\)
Download this page, D13 Partial Differentiation (PDF 139KB)
What's next... D14 Higher Order Derivatives
