D11 Small changes and approximations
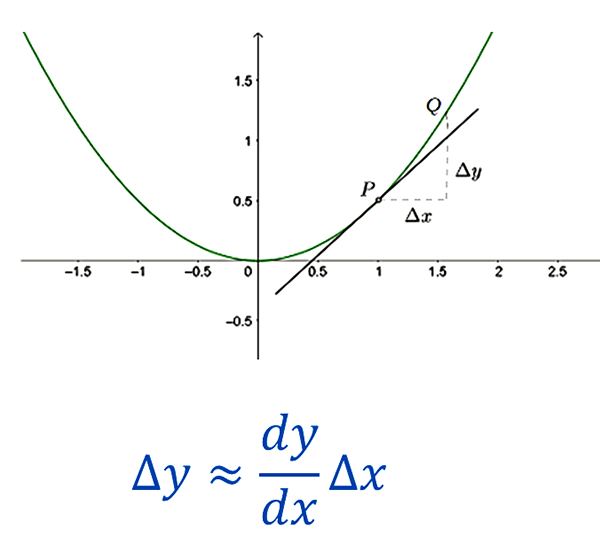
Sometimes a small change in one variable can render a big change in a larger value. For example, a small increase (or error) in the radius of a sphere means a lot more volume is added! If you estimate the small error in one variable, you can calculate the significant change in a larger variable by using derivatives.
The curve of any differentiable function will appear linear if observed over a sufficiently limited interval. If \(a\) is a point within that interval the tangent line through \((a,f(a))\) provides a reasonable approximation of values of \(f(x)\) providing \(x\) remains near \(a.\) A function that is differentiable at a specific point \((a,f(a))\) has a tangent line defined by the equation
\[ y=f(a)+f'(a)(x-a) \]
Using the tangent line to approximate a function is called
\[ L(x)=f(a)+f'(a)(x-a) \]
Example:
Consider the graph of the function \(f(x)=e^{2-x}\) near \(x=2.\)
Note that \(f'(x)=-e^{2-x}\)
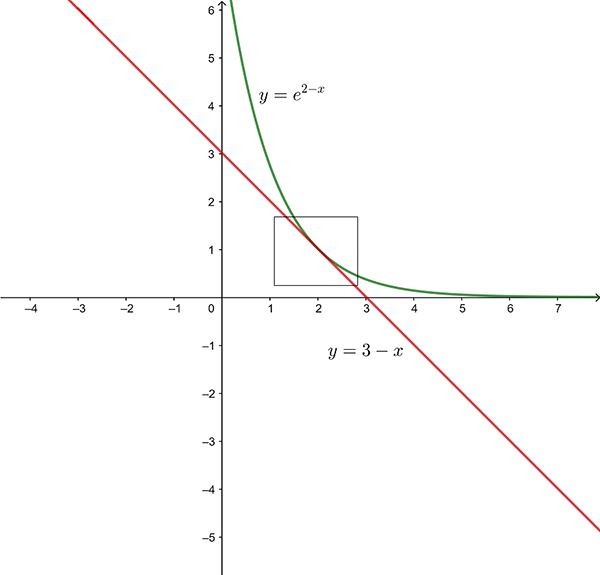
The tangent line at \(x=2\) is given by: \[\begin{align*} y & =f(2)+f'(2)(x-2)\\ y & =1+(-1)(x-2)\\ y & =3-x \end{align*}\]
For values of \(x\) near 2 the graph of the tangent line is close to the graph of \(f(x)=e^{2-x}\) and the tangent line can be used to approximate \(f(x).\)
If \(x=1.9\) , \(f(1.9)=e^{(2-1.9)}\approx1.105\). At \(x=1.9\) on the tangent line the value of \(y\) is \(y=3-1.9=1.1\)
If \(x=2.05\) , \(f(2.05)\approx0.951\). At \(x=2.05\) on the tangent line the value of \(y\) is \(0.95\)
Example:
\[\begin{align*} f(x)=\sqrt[3]{x} & \Rightarrow f'(x)=\frac{x^{-\frac{2}{3}}}{3}\\ f(8)=\sqrt[3]{8}=2 & \ and\ f'(8)=\frac{8^{-\frac{2}{3}}}{3}=\frac{1}{12}\\ L(x) & =f(a)+f'(a)(x-a)\\ L(7.98) & =2+\frac{1}{12}(7.98-8)\\ & =1.998 \end{align*}\]
Differentials
\(\triangle x\) is used to indicate a change in \(x\). \(\triangle y\) is used to indicate a change in \(y\). \(\triangle x\) and \(\triangle y\) are called differentials. Differentials can be used to estimate the amount a function will change as a result of a small change in \(x\).
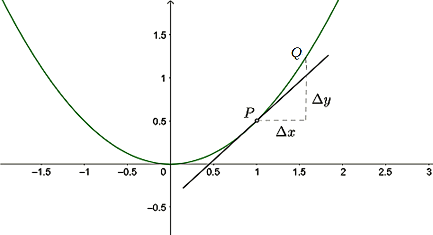
Consider the graph of the function \(y=f(x)\) above and the tangent to the function at the point P. As illustrated in the diagram for values of \(x\) close to \(1\) the slope of the tangent at \(1\), \(f'(1),\) is reasonably approximated by \(\frac{\triangle y}{\triangle x}\)
\[\begin{align*} \textrm{More generally, as}\triangle x\rightarrow0,\frac{\triangle y}{\triangle x} & \rightarrow\frac{dy}{dx}\\ \textrm{For small values of $\triangle$ x: }\triangle y & \approx\frac{dy}{dx}\triangle x \end{align*}\]
Examples
- The side of a square has length \(5\,cm.\) How much will the area of the square increase when the side length is increased by \(0.01\,cm\)?
Let the area of the square be\(A\) and let the length of a side be\(x\,cm\). Then \(A=x^{2}\) and \(\frac{dA}{dx}=2x.\) \[\begin{align*} \triangle A & \approx\frac{dA}{dx}\triangle x\\ & =2x\triangle x\\ & =2\times5\times0.01\\ & =0.1 \end{align*}\] The increase in area is approximately \(0.1\,cm^{2}\).
- A \(2\)% error is made in measuring the radius of a sphere. Find the percentage error in the volume?
Let the radius be \(r\) and the volume be \(V\) then \(\Delta r=0.02r.\) Since the volume of the sphere is given by \(V=\frac{4}{3}\pi r^{3},\) \(\frac{dV}{dr}=4\pi r^{2}.\)
First find \(\triangle V:\) \[\begin{align*} \triangle V & \approx\frac{dV}{dr}\triangle r\\ & =4\pi r^{2}\triangle r\\ & =4\pi r^{2}\times0.02r\\ & =0.08\pi r^{3} \end{align*}\] The percentage error in the volume: \[\begin{align*} \textrm{Percentage error in $V$ } & \approx\frac{\Delta V}{V}\times100\%\\ & =\frac{0.08\pi r^{3}}{\frac{4}{3}\pi r^{3}}\times100\%\\ & =\frac{0.08}{\frac{4}{3}}\times100\%\\ & =6\%. \end{align*}\] The percentage error in the volume is approximately 6%.
Exercises
Use linear approximation of the function \(f(x)=\sqrt{x}\) to find the approximate value of \(\sqrt{16.1}\)
Use linear approximation to find an approximate value of \(\cos59^{\circ}.\) (Hint: convert degrees to radians: \(1^{\circ}=\frac{\pi}{180}\,Radians.\))
If the radius of a sphere is increased from \(10\,cm\) to \(10.1\,cm\) what is the approximate increase in surface area?
The height of a cylinder is \(10\,cm\) and its radius is \(4\,cm\). Find the approximate increase in volume when the radius increases to \(\text{4.02}\,cm\).
An error of 3% is made in measuring the radius of a sphere. Find the percentage error in volume.
Hint: useful formula
Surface area of sphere , \(A=4\pi r^{2}\)
Volume of cylinder , \(V=\pi r^{2}h\)
Volume of sphere , \(V=\frac{4}{3}\pi r^{3}\)
4.0125
0.515
25.13 cm\(\textrm{$^{2}$ }\)
5.03cm\(^{3}\)
9%
Download this page, D11 Small Changes and Approximations (PDF 230KB)
What's next... D12 Implicit differentiation
