A2.1 Rearranging formulae
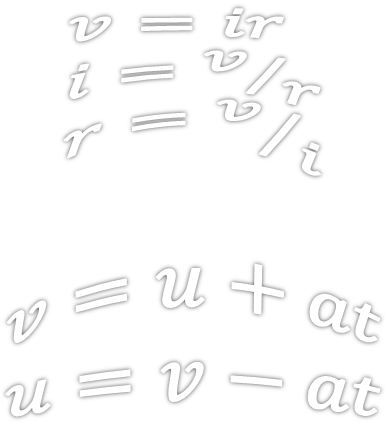
Learn how to manipulate or rearrange formulas that involve fractions and brackets.
A formula is a general rule giving the relationship between variables. The variables are represented by letters which provide us with a short hand way of writing the rule. Sometimes a formula is given in an inconvenient form and it’s necessary to change the subject of the formula. When we do this we need to use certain operations, so remember the following rules; minus undoes plus, plus undoes minus, division undoes multiplication, multiplication undoes division, square root undoes square and square undoes square root.
Let’s look at some examples to explain this. Let’s look at the formula A plus B equals C. Now let’s make A the subject, because we want to obtain A on its own we start by subtracting B so let’s use the rule minus undoes plus, so we have A plus B minus B equals C minus B, so from this we obtained A equals C minus B. Note we have to use minus B on both sides of the equation, remember the saying what we do to one side of the equation we must do to the other side of the equation so we have transposed the formula to find an expression for A.
Let’s look at another example. We have X minus Y equals Z and we want to make Y the subject. Notice we have a minus Y so let’s use the rule plus undoes minus, we write X minus Y plus Y equals Z plus Y. Note we have used plus Y on both sides of the equation so this leaves us with X equals Z plus Y, but we want Y on its own so we use the rule minus undoes plus again to get rid of Z so we have X minus Z equals Z minus Z plus Y which leaves us with X minus Z equals Y or rewriting that with Y on the left hand side we have Y equals X minus Z.
Let’s look at the formula for the area of a rectangle. The area of a rectangle is A equals L times W where A is the area, L is the length and W is the width of the rectangle. We say that A is the subject of the formula, let’s say we want to find the width, W, so we use the rule division undoes multiplication by dividing both sides by L. So let’s do that. We divide the left hand side by L, which is A over L and we divide the right hand side by L, so it’s L times W over L. So A over L is equal to W, notice that the Ls have cancelled out on the right hand side. If we swap the left hand side and the right hand side we have W equals A divided by L.
Let’s look at the formula M equals Q over P. M is the magnification of an object, Q is the size of the image and P is the size of the object. We want to find Q, the image size, so let’s use the rule multiplication undoes division, so if we multiply both sides by P we get M times P equals Q over P multiplied by P and this leaves us with M times P equals Q and so if we swap both left hand side and right hand side we get Q equals M times P.
That completes the film clip of transposition of formulas. Now go to the worksheet and try some exercises for yourself. Thank you.
Introduction
Some of the most important equations that we might be required to transpose occur frequently in science, engineering and economics. They are called formulae and give a general rule describing the relationship between variable quantities
Here are some examples: \[\begin{alignat*}{1} A= & \pi r^{2} \end{alignat*}\]
\[\begin{alignat*}{1} s & =ut+\frac{1}{2}at^{2} \end{alignat*}\]
\[\begin{alignat*}{1} S= & P(1+i)^{n} \end{alignat*}\]
In these examples \(A\), \(s\) and \(S\) are, respectively, the subjects of the formulae.1 \(A\), \(s\) and \(S\) are called subjects because they are on the left hand side of the formula and followed by an equal sign. Sometimes a formula is given in a particular form and it is necessary to rearrange the formula to make a different variable the subject:
We know the area of a circle \(A=\pi r^{2}\) where \(r\) is the radius and so we can calculate \(A\) for any value of \(r\). What if we know the area \(A\) and have to calculate the radius \(r\)?2 We need \(r\) to be the subject rather than \(A\).
We know \(s=ut+\frac{1}{2}at^{2}\) but what if we know \(s\) and \(t\) and want to calculate \(a\)?3 We need \(a\) to be the subject rather than \(s\).
Basic Rule
When rearranging equations and formulas, whatever you do on one side of the equal sign, you must do on the other.
Examples
Make \(A\) the subject in the formula \(A+B=C\).
Solution:4 We have to get rid of the \(B\) term on the left hand side to get \(A\) on its own. The \(B\) is being added to \(A\) on the left side so we subtract \(B\) from the left side to get rid of the \(B\) terms on the left. Our rule says we must subtract the \(B\) from the right side as well. \[\begin{align*} A+B & =C\\ A+B-B & =C-B\quad\textrm{subtracting $B$ from both sides}\\ A & =C-B. \end{align*}\]Make \(A\) the subject in the formula \(A-B=C\).
Solution:5 We have to get rid of the \(B\) term on the left hand side to get \(A\) on its own. The \(B\) is being subtracted from \(A\) on the left side so we add \(B\) to the left side to get rid of it. Our rule says we must add B to the right side as well. \[\begin{align*} A-B & =C\\ A-B+B & =C+B\quad\textrm{adding $B$ to both sides}\\ A & =C+B. \end{align*}\]Make \(A\) the subject in the formula \(AB=C\).
Solution:6 We have to get rid of the \(B\) term on the left hand side to get \(A\) on its own. The \(B\) is multiplying \(A\) on the left side so we divide by \(B\) on the left side to get rid of it. Our rule says we must divide by B on the right side as well. \[\begin{align*} AB & =C\\ \frac{AB}{B} & =\frac{C}{B}\quad\textrm{dividing both sides by $B$ }\\ A & =\frac{C}{B}\quad\textrm{cancelling the $B$ 's on the left side.} \end{align*}\]Make \(A\) the subject in the formula \(\frac{A}{B}=C\).
Solution:7 We have to get rid of the \(B\) term on the left hand side to get \(A\) on its own. The \(B\) is dividing \(A\) on the left side so we multiply by \(B\) on the left side to get rid of it. Our rule says we must multiply by B on the right side as well. \[\begin{align*} \frac{A}{B} & =C\\ \frac{AB}{B} & =BC\quad\textrm{multiplying both sides by $B$ }\\ A & =BC\quad\textrm{cancelling the $B$ 's on the left side.} \end{align*}\]Make \(A\) the subject of the formula \(A^{2}=B\).
Solution:8 This case involves \(A^{2}\). The inverse (opposite) operation to squaring is the square root. So to get A on its own we need to take the square root of both sides. \[\begin{align*} A^{2} & =B\\ \sqrt{A^{2}} & =\sqrt{B}\quad\textrm{taking the square root of both sides}\\ A & =\sqrt{B}. \end{align*}\]Make A the subject of the formula \(\sqrt{A}=B\).
Solution:9 This case involves \(\sqrt{A}\). The inverse (opposite) operation to the square root is squaring. So to get A on its own we need to square both sides. \[\begin{align*} \sqrt{A} & =B\\ \left(\sqrt{A}\right)^{2} & =B^{2}\\ A & =B^{2}. \end{align*}\]
Inverse operations
In the above examples we used operations to "undo" operations. Remember:
| subtraction undoes addition | conversely | addition undoes subtraction |
| division undoes multiplication | conversely | multiplication undoes division |
| square root undoes square | conversely | square undoes square root |
| \(\sqrt[n]{x}\) undoes \(x^{n}\) | conversely | \(x^{n}\) undoes \(\sqrt[n]{x}\) |
Also remember:
\(B+C=A\) is the same as \(A=B+C\) and
\(\sqrt{A^{2}}=A\) and \((\sqrt{B}){}^{2}\)= B. For example: \(\sqrt{3^{2}}=3\) and \(\left(\sqrt{25}\right)^{2}\)= 25.
Examples:
Transform \(V=A-K\) to make \(A\) the subject
Solution: \[\begin{alignat*}{1} V & =A-K\quad\mathrm{(we\,want\,\mathit{A}\,to\,be\,the\,subject)}\\ V+K & =A-K+K\mathrm{\quad(add}\,K\,\mathrm{to\,both\,sides)}\\ V+K & =A\\ A & =V+K\mathrm{\quad(making}\,A\,\mathrm{the\,subject)} \end{alignat*}\]Make \(d\) the subject of \(C=\pi d\) \[\begin{alignat*}{1} C & =\pi d\quad\mathrm{(we\,want\,\mathit{d}\,to\,be\,the\,subject)}\\ \frac{C}{\pi} & =\frac{\pi d}{\pi}\mathrm{\quad(divide\,both\,sides\,by\,\mathit{\pi}\,then\,cancelling)}\\ \frac{C}{\pi} & =d\\ d & =\frac{C}{\pi}\mathrm{\quad(making}\,d\,\mathrm{the\,subject)} \end{alignat*}\]
Rearrange \(j=3w-5\) in terms of \(w\) . \[\begin{alignat*}{1} j & =3w\text{\textendash}5\quad\mathrm{(we\,want\,\mathit{w}\,to\,be\,the\,subject)}\\ j+5 & =3w\text{\textendash}5+5\mathrm{\quad(add}\,5\,\mathrm{to\,both\,sides)}\\ j+5 & =3w\mathrm{\mathrm{\quad(giving}\,\textit{3w}\,as\,\mathrm{the\,subject)}}\\ \frac{j+5}{3} & =\frac{3w}{3}\mathrm{\quad(divide\,both\,sides\,by\,\mathit{3}\,then\,cancelling)}\\ \frac{j+5}{3} & =w\\ w & =\frac{j+5}{3}\mathrm{\quad(making}\,w\,\mathrm{the\,subject)} \end{alignat*}\]
Make \(c\) the subject of \(E=mc^{2}\). \[\begin{alignat*}{1} E & =mc^{2}\quad\mathrm{(we\,want\,\mathit{c}\,to\,be\,the\,subject})\\ \frac{E}{m} & =\frac{mc^{2}}{m}\mathrm{\quad(divide\,both\,sides\,by\,\mathit{m})}\\ \frac{E}{m} & =c^{2}\mathrm{\quad(cancelling)}\\ \sqrt{\frac{E}{m}} & =\sqrt{c^{2}}\quad\mathrm{(square\,root\,both\,sides)}\\ \sqrt{\frac{E}{m}} & =c\mathrm{\quad(remember}\,\sqrt{3^{2}}=3)\\ c & =\sqrt{\frac{E}{m}}\mathrm{\quad(rearanging\,}\mathrm{making}\,c\,\mathrm{the\,subject)} \end{alignat*}\]
Exercise
| 1. | \(m=n-2\) | Find \(n\) | \(\quad\) | 2. | \(A=2B+C\) | Find \(C\) | ||
| 3. | \(A=2B+C\) | Find \(B\) | \(\quad\) | 4. | \(P=\frac{k}{v}\) | Find \(K\) | ||
| 5. | \(PV=k\) | Find \(V\) | \(\quad\) | 6. | \(v=u+at\) | Find \(a\) | ||
| 7. | \(v=u+at\) | Find \(t\) | \(\quad\) | 8. | \(r=\sqrt{\frac{A}{\pi}}\) | Find \(A\) | ||
| 9. | \(A=x^{2}\) | Find \(x\) | \(\quad\) | 10. | \(A=\pi r^{2}\) | Find \(r\) |
| 1. | \(n=m+2\quad\quad\) | 2. | \(C=A-2B\qquad\) | 3. | \(B=\frac{A-C}{2}\qquad\) | 4. | \(k=PV\qquad\) | 5. | \(V=\frac{K}{P}\) | ||
| 6. | \(a=\frac{V-U}{t}\qquad\) | 7. | \(t=\frac{V-U}{a}\qquad\) | 8. | \(A=\pi r^{2\qquad}\) | 9. | \(x=\pm\sqrt{A}\qquad\) | 10. | \(r=\pm\sqrt{\frac{A}{\pi}}\) |
