A2.2 Rearranging formulas: Brackets and fractions
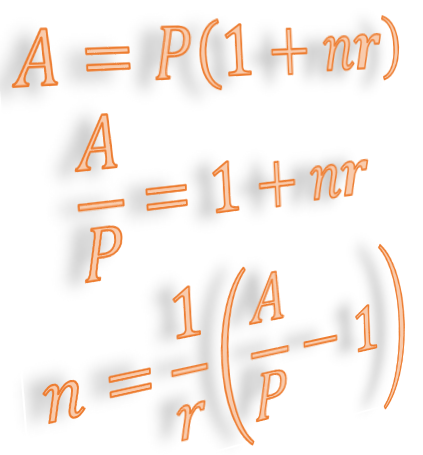
Rearranging formulas, also called transposition of formulas, is a necessary skill for most courses. This module provides essential skills in manipulating formulas.
Introduction
Formulas are used in many branches of economics, science and engineering. For example, the formula for simple interest is:1 Note that when we write \(nr\) we mean \(n\times r\). Most of the time we ignore the multiplication sign “\(\times\)” as it can be confused with \(x\). Also when we write \(A=P(1+nr)\) the \(P\) outside the bracket is multiplying everything in the bracket. That is we mean \(A=P\times\left(1+nr\right)\). For the same reason we do not write the multiply sign. \[ A=P(1+nr) \] Here, \(A\) is the amount you have after \(n\) time periods (months or years usually), \(P\) is the amount you invest, and \(r\) is the interest rate per time period. \(A\) is called the of the formula because the formula is in the form \(A\) is equal to … .
What about if we want \(P\) to be the subject? As a first step we could get rid of the \(\left(1+nr\right)\) term that is multiplying \(P\). The opposite of multiplication is division. To get rid of the \(\left(1+nr\right)\) we divide both sides of the formula by \(\left(1+nr\right)\).2 When rearranging formulas, the main rule is: whatever you do to one side you must do to the other.
What we get is:
\[ \frac{A}{(1+nr)}=\frac{P(1+nr)}{(1+nr)} \] Now the \((1+nr)\) terms can be canceled to get: \[ \frac{A}{(1+nr)}=P \] or \[ P=\frac{A}{(1+nr)} \]
When rearranging formulas, the starting point depends on the formula itself. We illustrate this in the examples below.
Examples:
Suppose you have $1000 to invest and you want to know how long it will take to get $2000 with an interest rate of 5% per year with simple interest.
The formula for simple interest is \[ A=P(1+rn) \] and we know A=$2000, \(P=\$1000\) and \(r=5%=5/100=0.05\). We want to find \(n\).
Solution:
Our first step is to get rid of the \(P\) that is multiplying the bracket \((1+rn)\). We do this by dividing both sides by \(P\) to get \[ \frac{A}{P}=\frac{P(1+rn)}{P}. \] Now we cancel the \(P\) to get 3 There is actually a 1 multiplying the bracket we never show it. Because multiplying by 1 does not change anything, we can remove the brackets as shown below. \[\begin{align*} \frac{A}{P} & =\left(1+rn\right)\\ & =1+rn. \end{align*}\] Next we want to get the \(rn\) on its own. We do this by subtracting 1 from both sides to get: \[\begin{align*} \frac{A}{P}-1 & =1+rn-1\\ & =rn. \end{align*}\] The last step is to get \(n\) on its own. We do this by dividing both sides by \(r\)4 Remember dividing by \(r\) is the same as multiplying by \(1/r\).
\[ \frac{1}{r}\left(\frac{A}{P}-1\right)=\frac{nr}{r}. \] Canceling the \(r\) on the right hand side gives: \[\begin{align*} \frac{1}{r}\left(\frac{A}{P}-1\right) & =n\\ n & =\frac{1}{r}\left(\frac{A}{P}-1\right). \end{align*}\] We can now calculate \(n\) by substituting the values for \(A\), \(P\) and \(r\): \[\begin{align*} n & =\frac{1}{r}\left(\frac{A}{P}-1\right)\\ & =\frac{1}{0.05}\left(\frac{2000}{1000}-1\right)\\ & =20. \end{align*}\] So it will take 20 years to double the initial $1000 investment!Transform the formula \(P=2(L-W)\) to make ‘\(L\)’ the subject.
Solution: \[\begin{align*} P & =2\left(L-W\right)\\ \frac{P}{2} & =\frac{2\left(L-W\right)}{2}\quad\left(\textrm{divide both sides by 2}\right)\\ \frac{P}{2} & =L-W\quad\left(\textrm{cancel the 2 and remove the brackets}\right)\\ \frac{P}{2}+W & =L-W+W\quad\left(\textrm{add $W$ to both sides}\right)\\ & =L\\ L & =\frac{P}{2}+W\quad\textrm{rearrange to put $L$ on the left}. \end{align*}\] Note that you don’t have to put explanations on each line in your solution. We include the notes to show you what we are doing.Transform the formula \(P=2(L-W)\) to make \(W\) the subject.
Solution: \[\begin{align*} P & =2\left(L-W\right)\\ \frac{P}{2} & =\frac{2\left(L-W\right)}{2}\quad\left(\textrm{divide both sides by 2}\right)\\ \frac{P}{2} & =L-W\quad\left(\textrm{cancel the 2 and remove the brackets}\right)\\ \frac{P}{2}-L & =L-W-L\quad\left(\textrm{subtract $L$ from both sides}\right)\\ & =-W\\ -W & =\frac{P}{2}-L\quad\textrm{$\left(\textrm{rearrange to put$-W$ on the left}\right)$ }\\ W & =-\frac{P}{2}+L\quad\textrm{$\left(\textrm{multiply both sides by $-1$ to get +$W$ on left}\right)$ }\\ & =L-\frac{P}{2}\quad\textrm{$\left(\textrm{rearrange terms (optional)}\right)$ .} \end{align*}\]Rearrange the formula \(L=\left(Mt-g\right)/b\) to make ‘M’ the subject.5 In this case the fraction bar on the right hand side acts like a bracket. That is the \(b\) on the bottom is dividing into the \(Mt\) and \(-g\) terms.
Solution: \[\begin{align*} L & =\frac{Mt-g}{b}\\ Lb & =Mt-g\quad\textrm{$\left(\textrm{multiplying both sides by $b$ and cancelling $b$ on right}\right)$ }\\ Lb+g & =Mt-g+g\quad\left(\textrm{adding $g$ to both sides}\right)\\ & =Mt\\ \frac{Lb+g}{t} & =M\quad\textrm{$\left(\textrm{dividing both sides by $t$ }\right)$ }\\ M & =\frac{Lb+g}{t}\quad\textrm{$\left(\textrm{rewrite to put M on left}\right)$ .} \end{align*}\]Make \(v\) the subject of \(E=mgh+\) \(\frac{1}{2}mv^{2}.\)
Solution:6 This example is a bit briefer and closer to what you should aim for because we are not showing things like \(mgh-mgh\) (which are equal to zero) on the third line of the solution. We also use a square root function (the opposite to squaring) to get \(v\) from \(v^{2}\) in the last line. Note that taking the square root of a positive number gives two possibilities - one positive, the other negative. Usually a formula will relate to a physical situation and the negative solution may not make sense. In this case, you take the positive solution as the answer. We do this in the last step of the solution. \[\begin{align*} E & =mgh+\frac{1}{2}mv^{2}\\ E-mgh & =\frac{1}{2}mv^{2}\quad\left(\textrm{subtracting $mgh$ from both sides}\right)\\ 2\left(E-mgh\right) & =mv^{2}\quad\left(\textrm{multiplying both sides by $2$ }\right)\\ \frac{2\left(E-mgh\right)}{m} & =v^{2}\quad\textrm{$\left(\textrm{dividing both sides by $m$ }\right)$ }\\ v^{2} & =\frac{2\left(E-mgh\right)}{m}\\ v & =\pm\sqrt{\frac{2\left(E-mgh\right)}{m}}\quad\textrm{$\left(\textrm{taking the square root of both sides}\right)$ }\\ & =\sqrt{\frac{2\left(E-mgh\right)}{m}}\quad\textrm{$\left(\textrm{taking the positive root as the answer.}\right)$ } \end{align*}\]If \(2/k=(j+1)/3,\) find \(k\).
Solution: Note that the fraction bar acts like a bracket. When we multiply both sides by \(k\) the \(j+1\) term is put into a bracket \[\begin{align*} \frac{2}{k} & =\frac{j+1}{3}\\ 2 & =\frac{k\left(j+1\right)}{3}\quad\textrm{$\left(\textrm{multiplying both sides by $k$ }\right)$ }\\ 6 & =k\left(j+1\right)\quad\left(\textrm{multiplying both sides by $3$ }\right)\\ \frac{6}{j+1} & =k\quad\left(\textrm{dividing both sides by $j+1$ }\right)\\ k & =\frac{6}{j+1}. \end{align*}\] It is possible to do the first two steps in one action as follows: \[\begin{align*} 6 & =k\left(j+1\right). \end{align*}\] This is called cross-multiplication.
Exercise
\(S=C(A+B)\text{, find $A$ .}\)
\(V=\frac{Ah}{3},\text{find }A.\)
\(A=\frac{h\left(a+b\right)}{2}\), find \(a.\)
\(A=\frac{2B+C}{P},\text{ find }B.\)
\(A=\frac{2P\left(B-C\right)}{3},\) find \(C\).
\(I=\frac{Mr^{2}}{2},\) find \(r.\)
\(H=k\left(1-bt\right)\), find \(b\).
\(t=2\pi\sqrt{\frac{h+k}{g}}\), find \(h.\)
\(v^{2}=u^{2}+2as\), find \(u.\)
\(m=\sqrt{\frac{x+y}{z}}\), find \(y.\)
\(A=\frac{S}{C}-B\)
\(A=\frac{3v}{h}\)
\(a=\frac{2A}{h}-b\)
\(B=\frac{AP-C}{2}\)
\(C=B-\frac{3A}{2P}\)
\(r=\pm\sqrt{\frac{2I}{m}}\)
\(b=\frac{k-H}{kt}\)
\(h=\frac{t^{2}g}{4\pi^{2}}-k\)
\(u=\pm\sqrt{v^{2}-2as}\)
\(y=m^{2}z-x\)
Download this page, A2.2 Rearranging formulas: Brackets and fractions (PDF 212KB)
