A3.6 Polynomial long division

One polynomial may be divided by another of lower degree (lower power indices) by long division (similar to arithmetic long division). This is another way to yield the factors of a quadratic.
At primary school you were probably exposed to long division, whereby a big number was divided by another big number. Sometimes this gave an integer result or sometimes a number plus a fraction. 1 An integer is a positive or negative whole number and may include \(0.\) For example in the case that the result was an integer we could have
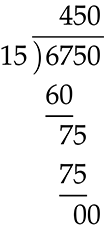
This means that \(6750\div15=450\) or \(6750=15\times450.\)
In case the numbers do not exactly divide we could have
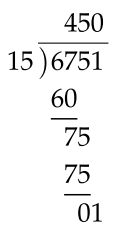
This means that \[\begin{align*} 6751\div15 & =450+\frac{1}{15} \end{align*}\] or, in decimal form, \[\begin{align*} 6751\div15 & =450.0\overline{6} \end{align*}\] where the over-bar on the \(6\) indicates it repeats.
In the age of calculators, long division of numbers is not so important. However it is still useful in factorising cubic (and higher degree) polynomials.2 The degree of a polynomial is the highest power to which the variable is raised. For example, \[\begin{align*} 5x^{4}+2x^{2}-3 \end{align*}\] is a polynomial of degree \(4.\) Polynomials of degree \(1,2\), \(3\) and \(4\) are called linear, quadratic, cubic and quartic respectively. This module describes how to divide a polynomial by a polynomial of lower degree using long division.
The Basic Approach
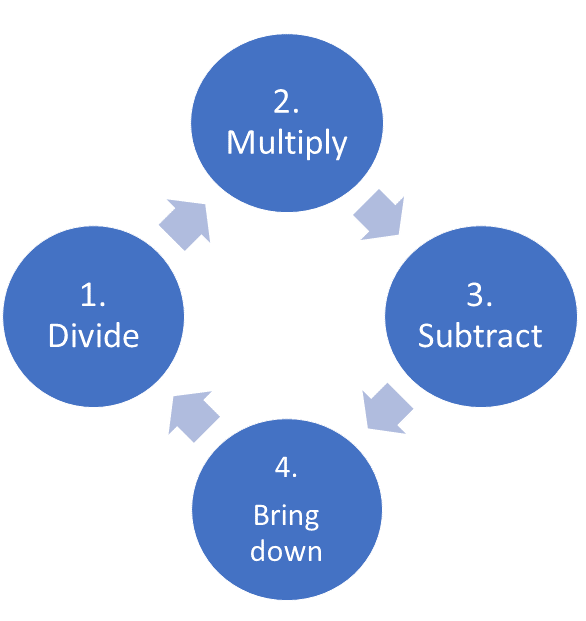
For long division, a useful algorithm, whether for numbers or polynomials is Divide, Multiply, Subtract, Bring Down.3 An algorithm is a series of instructions. If you look at long division on the web, you may find some differences. This is repeated until you obtain a remainder or zero and is illustrated below:
Example 1
Divide \(x^{2}-5x+6\) by \(x-3.\)
First we set up the long division by writing
\[\begin{array}{r} \\ x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \end{array}\]Now we start the algorithm: Divide, Multiply, Subtract and Bring down.
Divide
Divide the highest power of the polynomial \(x^{2}-5x+6\) by the highest power in the polynomial \(x-3.\) That is divide \(x^{2}\) by \(x\) to get \(x.\) Place the \(x\) as follows:
\[\begin{array}{r} x\phantom{)-2} \\ x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \end{array}\]Multiply
Multiply \(x-3\) by \(x\) to get \(x^{2}-3x\) and write the result as shown below:
\[\begin{array}{r} x\phantom{)-2} \\ x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \\ \underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \end{array}\]Subtract
Subtract \(x^{2}-3x\) from \(x^{2}-5x\) to get \(-2x\) as shown below:
\[\begin{array}{r} x\phantom{)-2} \\ x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \\ \underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \\ 0\,\,\,-2x\phantom{)+6} \end{array}\]Bring Down
Bring down the \(6\) and write as follows:
\[\begin{array}{r} x\phantom{)-2} \\ x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \\ \underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \\ 0-2x+6\phantom{)} \end{array}\]We now go back to the divide step and continue the algorithm until we get a remainder or zero.
Divide
Divide \(-2x\) by the leading term in \(x-3\) to get \(-2.\) That is divide \(x\) into \(-2x\) to get \(-2\) and write the \(-2\) on the top line as shown below.
\[\begin{array}{r} x-2\phantom{)} \\ x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \\ \underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \\ 0-2x+6\phantom{)} \end{array}\]Multiply
Multiply \(x-3\) by \(-2\) to get\(-2x+6\) and write this as shown below.
\[\begin{array}{r} x-2\phantom{)} \\ x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \\ \underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \\ 0-2x+6\phantom{)} \\ \underline{~\phantom{()}(-2x+6)} \end{array}\]Subtract
Subtract \(-2x+6\) from \(-2x+6\) to get \(0.\) This is the end of the process and, in this case there is no remainder.
\[\begin{array}{r} x-2\phantom{)} \\ x-3{\overline{\smash{\big)}\,x^2-5x+6\phantom{)}}} \\ \underline{-~\phantom{(}(x^2-3x)\phantom{-b)}} \\ 0-2x+6\phantom{)} \\ \underline{-~\phantom{()}(-2x+6)} \\ 0+0\phantom{)} \end{array}\]This is the end of the process and, in this case, there is no remainder. That means that \(x-3\) divides \(x^{2}-5x+6\) exactly and the answer is \(x-2.\) In other words4 Note that in this case it would be much easier to just factorise the quadratic or use the quadratic formula to get the same result. However, this is not available to us in general when the polynomials have higher degree. This is discussed in the next section. \[\begin{align*} \left(x-3\right)\left(x-2\right) & =x^{2}-5x+6. \end{align*}\]
Dividing a Higher Order Polynomial
The basic approach described above may be used on higher order polynomials. Generally the most common case is dividing a cubic polynomial by a linear polynomial We show this in the following example.
Example 2
Divide \(\left(x^{3}-6x^{2}+11x-6\right)\) by \(\left(x-1\right)\).
First we write the long division as shown below:
\[\begin{array}{r} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \end{array}\]We then apply the steps of the algorithm: Divide, Multiply, Subtract, Bring down.
Divide
Divide the highest term of \(x-1\) into the highest term of \(x^{3}-6x^{2}+11x-6\). That is divide \(x\) into \(x^{3}\) to get \(x^{2}\) and write
\[\begin{array}{r} x^2\phantom{\,-5\,x+6)x} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \end{array}\]Multiply
Multiply \(x^{2}\) by \(x-1\) to get \(x^{3}-x^{2}\) and write as below:
\[\begin{array}{r} x^2\phantom{\,-5\,x+6)x} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\ \underline{(x^3-\,\, x^2)\phantom{bbbbbbbbbi)}} \end{array}\]Subtract
Subtract \(x^{3}-x^{2}\) from \(x^{3}-6x^{2}\) to get \(-5x^{2}\)and write as:
\[\begin{array}{r} x^2\phantom{\,-5\,x+6)x} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\ \underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbbi)}} \\ 0- \, \, 5x^2\phantom{bbbi+11x)} \end{array}\]Bring Down
Bring down the \(11x\) term and write as:
\[\begin{array}{r} x^2\phantom{\,-5\,x+6)x} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\ \underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbbi)}} \\ \, \, -5x^2+11x\phantom{bbbi)} \end{array}\]Divide
We now repeat the algorithm. We divide the highest power of \(x-1\) into \(-5x^{2}\). That is, we divide \(x\) into \(-5x^{2}\) to get \(-5x\) and write as follows.
\[\begin{array}{r} x^2\,\,-5x\phantom{)+6} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\ \underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbbi)}} \\ 0- \, \, 5x^2+11x\phantom{bbbi)} \end{array}\]Multiply
Multiply \(-5x\) by \(x-1\) to get \(-5x^{2}+5x\) and write:
\[\begin{array}{r} x^2\,-5\,x\phantom{)+6} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\ \underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbbi)}} \\ \, \, -5x^2+11x\phantom{bbbi)} \\ \underline{~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)} \end{array}\]Subtract
Subtract \(-5x^{2}+5x\) from \(-5x^{2}+11x\) to get \(6x\) and write:
\[\begin{array}{r} x^2\,-5\,x\phantom{)+6} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}}\\ \underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbi)}}\\ - \, \, 5x^2+11x\phantom{bbbi)}\\ \underline{-~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)}\\ 6x \phantom{)-6} \end{array}\]Bring Down
Bring down the \(-6\) and write as
\[\begin{array}{r} x^2\,-5\,x\phantom{)+6} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\ \underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbi)}}\\ 0- \, \, 5x^2+11x\phantom{bbbi)}\\ \underline{-~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)}\\ 6x-6 \phantom{)} \end{array}\]Divide
Divide the leading term of \(x-1\) into the leading term of \(6x-6.\) That is divide \(x\) into \(6x\) to get \(6\) and write as follows:
\[\begin{array}{r} x^2\,-5\,x+6\phantom{)} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}}\\ \underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbi)}}\\ 0- \, \, 5x^2+11x\phantom{bbbi)} \\ \underline{-~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)}\\ 6x-6 \phantom{)} \end{array}\]Multiply
Multiply \(x-1\) by \(6\) and write as follows:
\[\begin{array}{r} x^2\,-5\,x+6\phantom{)} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\ \underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbi)}} \\ 0- \, \, 5x^2+11x\phantom{bbbi)} \\ \underline{-~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)} \\ 6x-6 \phantom{)} \\ \underline{\phantom{()}(6x-6)} \end{array}\]Subtract
Subtract \(6x-6-\left(6x-6\right)\) to get \(0\) and write as follows:
\[\begin{array}{r} x^2\,-5\,x+6\phantom{)} \\ x-1{\overline{\smash{\big)}\,x^3-6x^2+11x-6\phantom{)}}} \\ \underline{-(x^3-\,\, x^2)\phantom{bbbbbbbbi)}} \\ 0- \, \, 5x^2+11x\phantom{bbbi)} \\ \underline{-~\phantom{()}(-5x^2+\,\,5x)}\phantom{bbb)}\\ 6x-6 \phantom{)} \\ \underline{-~\phantom{()}(6x-6)} \\ 0+0\phantom{)} \end{array}\]As there are no more terms to bring down, we stop the algorithm. Our result is that \[\begin{align*} \left(x^{3}-6x^{2}+11x-6\right)\div\left(x-1\right) & =x^{2}-5x+6. \end{align*}\]
This is the same as \[\begin{align*} x^{3}-6x^{2}+11x-6=\left(x^{2}-5x+6\right)\left(x-1\right). \end{align*}\]
This is probably the best interpretation as we can then factorise the quadratic term on the RHS to get \[\begin{align*} x^{3}-6x^{2}+11x-6 & =\left(x^{2}-5x+6\right)\left(x-1\right)\\ & =\left(x-3\right)\left(x-2\right)\left(x-1\right). \end{align*}\] Which is of value when we are trying to graph \(x^{3}-6x^{2}+11x-6\) as it gives us the \(x-\)intercepts of the function.
Example 3
Divide \(\left(2x^{3}-3x+1\right)\) by \(\left(x-1\right)\).
The major difference from example 2 above is that there is no \(x^{2}\) term in \[\begin{align*} 2x^{3}-3x+1. \end{align*}\] We get around this by writing \[\begin{align*} 2x^{3}-3x+1 & =2x^{3}+0x^{2}-3x+1 \end{align*}\]
That is, we set up the long division as
\[\begin{array}{r} \\ x-1{\overline{\smash{\big)}\,2x^3+0x^2-3x+1\phantom{)}}} \end{array}\]and apply the algorithm used in Example 1 and 2 above.
Applying the algorithm we obtain:
\[\begin{array}{r} 2x^2+2x-1\phantom{)} \\ x-1{\overline{\smash{\big)}\,2x^3+0x^2-3x+1\phantom{)}}} \\ \underline{-(2x^3- 2x^2)\phantom{bbbbbbbi)}}\\ 0+ \, \, 2x^2-3x\phantom{bbbi)} \\ \underline{-~\phantom{()}(2x^2-2x)}\phantom{bbb)} \\ 0-\,\, x\,\,+1 \phantom{)} \\ \underline{-~\phantom{()}(-x\,\,+1)} \\ 0\,\,+0\phantom{)} \end{array}\]Hence we see that \[\begin{align*} \left(2x^{3}-3x+1\right)\div\left(x-1\right) & =2x^{2}+2x-1 \end{align*}\] or \[\begin{align*} 2x^{3}-3x+1 & =\left(2x^{2}+2x-1\right)\times\left(x-1\right). \end{align*}\]
In your work, the final result as shown above is all that is required. That is you would write:
\[\begin{array}{r} 2x^2+2x-1\phantom{)} \\ x-1{\overline{\smash{\big)}\,2x^3+0x^2-3x+1\phantom{)}}} \\ \underline{-(2x^3- 2x^2)\phantom{bbbbbbbi)}} \\ 0+ \, \, 2x^2-3x\phantom{bbbi)} \\ \underline{-~\phantom{()}(2x^2-2x)}\phantom{bbb)} \\ 0-\,\, x\,\,+1 \phantom{)} \\ \underline{-~\phantom{()}(-x\,\,+1)} \\ 0\,\,+0\phantom{)} \end{array}\]The steps (divide, multiply, subtract, bring down) identified in Examples \(1\) and \(2\) are for explanation only. You do not have to make reference to them.
Please try Exercise 1.
The Factor Theorem
Solution of a cubic equation is frequently required in maths, science and engineering.
The long division of polynomials described above is an important tool in this. However the Factor Theorem is equally important.
The Factor Theorem states:
If \(P(x)\) is a polynomial in \(x\) and \(P(a)=0\) then \((x-a)\) is a factor of \(P(x)\). We can use the factor theorem to find one factor of a polynomial, and then use polynomial long division to find the remaining factor(s).
Example 4
Solve the equation \(x^{3}-5x^{2}-2x+24=0.\)
We first use the Factor Theorem to try and get a linear factor of \(x^{3}-5x^{2}-2x+24.\) Let \[ P\left(x\right)=x^{3}-5x^{2}-2x+24 \] then letting \(x=1,\) \[\begin{align*} P\left(1\right) & =1-5-2+24\\ & =18\\ & \neq0 \end{align*}\] and so \(\left(x-1\right)\) is not a factor of \(x^{3}-5x^{2}-2x+24\).
Now try \(x=-1\) to get, \[\begin{align*} P\left(-1\right) & =-1-5+2+24\\ & =20\\ & \neq0 \end{align*}\] and so \(\left(x-\left(-1\right)\right)=\left(x+1\right)\) is not a factor of \(x^{3}-5x^{2}-2x+24\).
Now try \(x=2\) to get \[\begin{align*} P\left(2\right) & =8-20-4+24\\ & =8\\ & \neq0 \end{align*}\] and so \(\left(x-2\right)\) is not a factor of \(x^{3}-5x^{2}-2x+24\).
Now try \(x=-2\) to get \[\begin{align*} P\left(-2\right) & =-8-20+4+24\\ & =0 \end{align*}\] and so \(\left(x-\left(-2\right)\right)=x+2\) is factor of \(x^{3}-5x^{2}-2x+24\). We now use polynomial division to divide \(x^{3}-5x^{2}-2x+24\) by \(x+2.\) We have
\[\begin{array}{r} x^2-7x+12\phantom{)} \\ x+2{\overline{\smash{\big)}\,x^3-5x^2-2x+24\phantom{)}}} \\ \underline{-(x^3+ 2x^2)\phantom{bbbbbbbbbi)}} \\ 0- 7x^2 \,-2x\phantom{bbbbi)} \\ \underline{-~\phantom{()}(-7x^2-\!14x)}\phantom{bbbi)} \\ 12x+24 \phantom{)} \\ \underline{-~\phantom{()}(12x+24)} \\ 0+0\phantom{)} \end{array}\]That is, \[\begin{align*} \left(x^{3}-5x^{2}-2x+24\right)\div\left(x+2\right) & =\left(x^{2}-7x+12\right)\\ x^{3}-5x^{2}-2x+24 & =\left(x^{2}-7x+12\right)\left(x+2\right) \end{align*}\] The quadratic on the RHS may be factorised as 5 This can be done by inspection, or more formally using the quadratic formula which says for a quadratic equation: \[\begin{align*} ax^{2}+bx+c & =0,\\ x & =\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}. \end{align*}\] In our case \[\begin{align*} x & =\frac{-\left(-7\right)\pm\sqrt{49-4\left(1\right)12}}{2}\\ & =\frac{7\pm\sqrt{1}}{2}\\ & =4\text{ or $3$ .} \end{align*}\] \[\begin{align*} x^{2}-7x+12 & =\left(x-4\right)\left(x-3\right) \end{align*}\] and so \[\begin{align*} x^{3}-5x^{2}-2x+24 & =\left(x-4\right)\left(x-3\right)\left(x+2\right). \end{align*}\] Hence the solutions to \(x^{3}-5x^{2}-2x+24=0\), are \(x=4\), \(x=3\) and \(x=-2.\)
Please try Exercise 2 below.
Exercise 1
\(\quad\)a. Divide \(2x^{3}-6x^{2}+5x+2\) by \(x-2\).
Divide \(3x^{3}+13x^{2}+6x-12\) by \(3x+4\)
Divide \(3x^{3}+x-1\) by \(x-1\)
Divide \(x^{3}+2x-3\) by \(x-1\)
Divide \(2x^{4}+5x^{3}+x+3\) by \(2x+1\)
Divide \(2x^{3}+x^{2}+5x+12\) by \(2x+3\)
\(\quad\)a. \(2x^{2}-2x+1\) with remainder \(4.\)
\(x^{3}+3x-2\) with remainder \(-4\)
\(3x^{2}-3x+4\) with remainder \(-3\)
\(x^{2}+x+3\) with remainder \(0\)
\(x^{3}+2x^{2}-x+1\) with remainder \(2\)
\(x^{2}-x+4\) with remainder \(0.\)
Exercise 2
Solve the following equations:
\(x^{3}+7x^{2}+11x+5=0\)
\(4x^{3}+2x^{2}-2x=0\)
\(-x^{3}-3x^{2}+x+3=0\)
\(x^{3}-7x-6=0\)
\(\quad\)a. \(x=-1,\ x=-5\)
\(x=0,\ x=-1,\ x=1/2\)
\(x=1,\ x=-3,\ x=-1\)
\(x=-1,\ x=-2,\ x=3\)
Download this page: A3.6 Factorisation of Polynomials Using Long Division (PDF 299KB)
