A3.5 Completing the square

Another way to factorise a quadratic expression (of the form x2 + bx + c) is by the method of "completing the square".
Hi, I’m Martin Lindsay from the Study and Learning Centre at RMIT University. This is another factorisation movie. This one is on completing the square.
Let’s first look at X plus B all squared, which is the same as X squared plus two B X plus B squared, or putting it around the other way, X squared plus two B X plus B squared is the same as X plus B all squared. Notice the term B is half of the co‑efficient of X, the middle term. In other words X plus B all squared is called a perfect square. So as an example, X squared minus 24 X plus 144, look at the middle term which is minus 24 X, half of that is minus 12 and thus that is our perfect square. So knowing how to find a perfect square is very important when completing the square.
Let’s do an example. Factorise X squared plus eight X minus nine. Step one, half the co-efficient of X, in other words half of eight is four, then we square the result, four squared is 16. Step three, add and subtract 16, in other words X square plus eight X plus 16 is our perfect square, then we subtract the 16 minus nine, notice that expression there is the same as the original expression, eight square plus eight X minus nine. Step four, complete the square and simplify. In other words eight square plus eight X plus 16 is X plus four all squared minus 16 minus nine is minus 25 and then finally factorise using the difference of two squares, which is X plus four plus five brackets X plus four minus five, which is the same as X plus four X minus one.
Let’s do another one. X squared minus six X minus four. Step one, half the co‑efficient of X which is half of six is three, square the result, three squared is nine. Step three, add and subtract nine, that gives us X squared minus six X plus nine, there’s our perfect square, then we have to subtract nine to make sure that we have the original X squared minus six X minus four. Step four, complete the square and simplify, in other words, X squared minus six X plus nine is X minus three all squared minus nine minus four is minus 13 and then finally factorise using the difference of two squares, which is X minus three plus root 13, X minus three minus root 13.
Now let’s look at a slightly harder problem. Notice here we’re factorising two X squared minus 10 X plus two. We can only complete the square if the co-efficient of X squared is one, so the first step we have to do is to remove the factor of two, thus we have two brackets X squared minus five X plus one. Now we go through the same process as before, half the co-efficient of X, but here the co-efficient of X is now five, so that half of that is five over two, square the result, five over two squared is 25 over four, then we add and subtract 25 over four which gives us that expression. Continuing on from the previous slide we have that expression, now we need to take the difference of two squares which gives us two brackets X minus five over two all squared minus 21 over four, but that can be simplified into the final expression two brackets X minus five over two plus root 21 over two brackets X minus five over two minus root 21 over two.
Now try some questions for yourself. The answers to these problems are on the next slide. Thanks for watching this short movie.
A perfect square is of the form: \[\begin{align*} \left(x+b\right)^{2} & =x^{2}+2bx+b^{2}. & \left(1\right) \end{align*}\] or \[\begin{align*} \left(x-b\right)^{2} & =x^{2}-2bx+b^{2}. & \left(2\right) \end{align*}\]
Consider, the expression \[\begin{align*} x^{2}+2bx. \end{align*}\] To make this a perfect square, according to eqn \(\left(1\right),\) you have to add \(b^{2}\). But if you add \(b^{2}\) you must also take it away to preserve equality. That is, given \(x^{2}+2bx\) we can write: \[\begin{align*} x^{2}+2bx & =x^{2}+2bx+b^{2}-b^{2}. & \left(3\right) \end{align*}\]
Note that the amount we added and subtracted is one half of the \(x\) coefficient squared. That is,
\[\begin{align*} \left(\frac{2b}{2}\right)^{2} & =b^{2}. \end{align*}\]
If you look at the right hand side of eqn \(\left(3\right)\)we have added \(b^{2}-b^{2}=0\) so the value is unchanged. However we can now group the terms to get:
\[\begin{align*} x^{2}+2bx & =\left(x^{2}+2bx+b^{2}\right)-b^{2}. \end{align*}\] Using eqn \(\left(1\right)\) above the term in brackets on the right hand side is \(\left(x+b\right)^{2}\)and so using the difference of two squares formula (DOTS) 1 The difference of two squares formula states that \[\begin{align*} a^{2}-b^{2} & =\left(a+b\right)\left(a-b\right)\\ & =\left(a-b\right)\left(a+b\right). \end{align*}\] Note that the order of the factors on the right hand side does not matter. \[\begin{align*} x^{2}+2bx & =\left(x+b\right)^{2}-b^{2}\\ & =\left(x+b-b\right)\left(x+b+b\right)\\ & =x\left(x+2b\right). \end{align*}\]
At first this might seem like a lot of work for very little gain. After all, it is pretty obvious that \[\begin{align*} x^{2}+2bx & =x\left(x+2b\right). \end{align*}\]
Completing the Square
The advantage of completing the square comes in when we have to factorise something like \(x^{2}+2bx+c\) where \(c\) is a real number. In order to do this we follow the above procedure and the results are magical! The following examples illustrate this.
Example 1
Factorise \(x^{2}+8x-5\) by completing the square.
Solution:
We take half of the \(x\) coefficient and square it. We then add and subtract it from the right hand side to get \[\begin{align*} x^{2}+8x-5 & =x^{2}+8x-5+\left(\frac{8}{2}\right)^{2}-\left(\frac{8}{2}\right)^{2}\quad\text{(add the square of half the $x\text{ coefficient and subtract it)}$ }\\ & =x^{2}+8x-5+\left(4\right)^{2}-\left(4\right)^{2}\\ & =x^{2}+8x+\left(4\right)^{2}-5-\left(4\right)^{2}\ (\text{regroup the terms on the RHS)}\\ & =\left(x^{2}+8x+\left(4\right)^{2}\right)-5-16\\ & =\left(x+4\right)^{2}-21\ \text{using eqn $\left(1\right)$ }\\ & =\left(x+4\right)^{2}-\left(\sqrt{21}\right)^{2}\\ & =\left(x+4-\sqrt{21}\right)\left(x+4+\sqrt{21}\right) \end{align*}\] where, in the last line, we used the DOTS rule.
Example 2
Factorise \(x^{2}-6x-4\) by completing the square.
Solution:
We take half of the \(x\) coefficient and square it. We then add and subtract this from the right hand side to get \[\begin{align*} x^{2}-6x-4 & =x^{2}-6x-4+\left(-3\right)^{2}-\left(-3\right)^{2}\\ & =x^{2}-6x-4+9-9\\ & =x^{2}-6x+9-4-9\\ & =\left(x-3\right)^{2}-13\ \text{using eqn $\left(2\right)$ }\\ & =\left(x-3\right)^{2}-\left(\sqrt{13}\right)^{2}\\ & =\left(x-3+\sqrt{13}\right)\left(x-3-\sqrt{13}\right)\ \text{using DOTS rule.} \end{align*}\]
Example 3
Factorise \(x^{2}+5x+9\) by completing the square.
Solution:
We take half of the \(x\) coefficient and square it. We then add and subtract this from the right hand side to get \[\begin{align*}
x^{2}+5x+9 & =x^{2}+5x+9+\left(\frac{5}{2}\right)^{2}-\left(\frac{5}{2}\right)^{2}\\
& =x^{2}+5x+\left(\frac{5}{2}\right)^{2}+9-\left(\frac{5}{2}\right)^{2}\\
& =\left(x+\frac{5}{2}\right)^{2}+9-\frac{25}{4}\ \text{using eqn $\left(1\right)$ }\\
& =\left(x+\frac{5}{2}\right)^{2}+\frac{11}{4}.
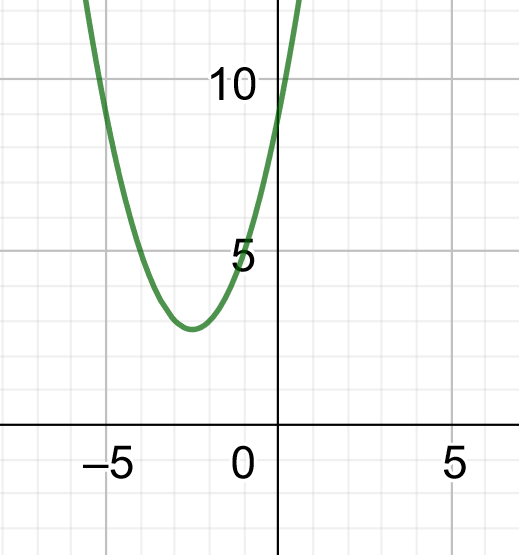
\end{align*}\] We are in trouble here. We cannot apply the DOTS rule because we have the SUM of two squares not the DIFFERENCE. So in this case the quadratic \(x^{2}+5x+9\) does not have any real factors and solutions. Complex factors and solutions do exist but are not considered in this module.2 Geometrically this means that the graph of \(x^{2}+5x+9\) does not intersect the \(x-\) axis. The graph is shown below
See Exercise 1 below.
Completing the Square when the Coefficient of \(x^{2}\) is not One
In this section we consider the completing the square method on quadratics of the form \(ax^{2}+bx+c\) where \(a\neq1.\) In this case we simply divide the quadratic by \(a\) and proceed as above. That is we write
\[\begin{align*} ax^{2}+bx+c & =a\left[x^{2}+\frac{b}{a}x+\frac{c}{a}\right] \end{align*}\] and complete the square on the RHS term in the square brackets. Don’t forget to include the \(a\) in the final result!
Example 4
Factorise \(2x^{2}-10x+2\).
Solution:
Divide the quadratic by \(2\) and write \[\begin{align*} 2x^{2}-10x+2 & =2\left[x^{2}-\frac{10}{2}x+\frac{2}{2}\right]\\ & =2\left[x^{2}-5x+1\right]. \end{align*}\] Now complete the square on the quadratic in square brackets on the RHS, \[\begin{align*} 2x^{2}-10x+2 & =2\left[x^{2}-5x+1+\left(\frac{-5}{2}\right)^{2}-\left(\frac{-5}{2}\right)^{2}\right]\quad\text{(add the square of half the $x\text{ coefficient and subtract it)}$ }\\ & =2\left[x^{2}-5x+1+\frac{25}{4}-\frac{25}{4}\right]\\ & =2\left[x^{2}-5x+\frac{25}{4}+1-\frac{25}{4}\right]\ (\text{regrouping the terms on the RHS)}\\ & =2\left[\left(x-\frac{5}{2}\right)^{2}+1-\frac{25}{4}\right]\ \text{using eqn $\left(1\right)$ }\\ & =2\left[\left(x-\frac{5}{2}\right)^{2}-\frac{21}{4}\right]\\ & =2\left[\left(x-\frac{5}{2}\right)^{2}-\left(\frac{\sqrt{21}}{2}\right)^{2}\right]\\ & =2\left[\left(x-\frac{5}{2}+\frac{\sqrt{21}}{2}\right)\left(x-\frac{5}{2}-\frac{\sqrt{21}}{2}\right)\right]\ \text{using DOTS rule}\\ & =2\left(x-\frac{5}{2}+\frac{\sqrt{21}}{2}\right)\left(x-\frac{5}{2}-\frac{\sqrt{21}}{2}\right). \end{align*}\]
See Exercise 2 below.
Completing the Square and the Quadratic Formula
This section is beyond the intent of this module and may be skipped if you are not interested.
You may be aware of the quadratic formula. It gives the solutions of the quadratic equation: \[\begin{align*} ax^{2}+bx+c & =0 & \left(4\right) \end{align*}\] and is usually written as \[\begin{align*} x & =\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}. \end{align*}\] The quadratic formula is established by completing the square on eqn \(\left(4\right)\). To see this, we write \[\begin{align*} 0 & =ax^{2}+bx+c\\ & =x^{2}+\frac{b}{a}x+\frac{c}{a}\ \text{assuming $a\neq0$ }\\ & =x^{2}+\frac{b}{a}x+\frac{c}{a}+\left(\frac{b}{2a}\right)^{2}-\left(\frac{b}{2a}\right)^{2}\\ & =x^{2}+\frac{b}{a}x+\left(\frac{b}{2a}\right)^{2}+\frac{c}{a}-\left(\frac{b}{2a}\right)^{2}\ (\text{regrouping the terms on the RHS)}\\ & =\left(x+\frac{b}{2a}\right)^{2}+\frac{c}{a}-\left(\frac{b}{2a}\right)^{2}\ \text{using eqn $\left(1\right)$ }\\ & =\left(x+\frac{b}{2a}\right)^{2}+\frac{c}{a}-\frac{b^{2}}{4a^{2}}\\ & =\left(x+\frac{b}{2a}\right)^{2}+\frac{4ac-b^{2}}{4a^{2}}\\ \left(x+\frac{b}{2a}\right)^{2} & =-\left(\frac{4ac-b^{2}}{4a^{2}}\right)\\ & =\frac{b^{2}-4ac}{4a^{2}}\\ x+\frac{b}{2a} & =\pm\sqrt{\frac{b^{2}-4ac}{4a^{2}}}\\ & =\pm\frac{\sqrt{b^{2}-4ac}}{2a}\\ x & =-\frac{b}{2a}\pm\frac{\sqrt{b^{2}-4ac}}{2a}\\ & =\frac{-b\pm\sqrt{b^{2}-4ac}}{2a}\,, \end{align*}\] and so establishes the quadratic formula.
Exercise 1
Factorise by completing the square (if possible).
\(\text{a)$\,x^{2}+6x-5\qquad\text{b)$\,x^{2}+4x+2\qquad\text{c)$\,a^{2}-8a-2\qquad\text{d)$\,x^{2}+6x+10$ }$ }$ }$ }\)
\(\text{e)$\,x^{2}-5x+5\qquad\text{f)$\,y^{2}+3y+4\qquad\text{g)$\,a^{2}-5a-1.$ }$ }$ }\)
\(\text{a)$\,\left(x+3+\sqrt{14}\right)\left(x+3-\sqrt{14}\right)\qquad\text{b)$\,\left(x+2+\sqrt{2}\right)\left(x+2-\sqrt{2}\right)$ }$ }\)
\(\text{c)$\,\left(a-4+3\sqrt{2}\right)\left(a-4-3\sqrt{2}\right)$ $\qquad\text{d) No real factors}$ }\)
\(\text{e)$\,\left(x-\frac{5}{2}+\frac{\sqrt{5}}{2}\right)\left(x-\frac{5}{2}-\frac{\sqrt{5}}{2}\right)\qquad\text{f)$\,\text{No real factors.}$ }$ }\)
\(\text{g)$\,\left(a-\frac{5}{2}+\frac{\sqrt{29}}{2}\right)\left(a-\frac{5}{2}-\frac{\sqrt{29}}{2}\right)$ }\)
Exercise 2
Factorise by completing the square (if possible).
\(\text{a)$\,4x^{2}+8x-20\qquad\text{b)$\,x^{2}-6x+2\qquad\text{c)$\,12-4x-2x^{2}$ }$ }$ }\)
\(\text{a)$\,4\left(x+1+\sqrt{6}\right)\left(x+1-\sqrt{6}\right)$ }\qquad\text{b)$\,\left(x-3+\sqrt{7}\right)\left(x-3-\sqrt{7}\right)$ }\qquad\text{c)$\,-2\left(x+1+\sqrt{7}\right)\left(x+1-\sqrt{7}\right)$ }\)
Download this page, A3.5 Factorisation: Completing the Square (PDF 179 KB)
What's next... Polynomial long division
