A1.3 Removing brackets
What do I do with the brackets?
Brackets are useful to group numbers, pronumerals and operations together as a whole. Whatever is around the brackets affects all the things inside the brackets.
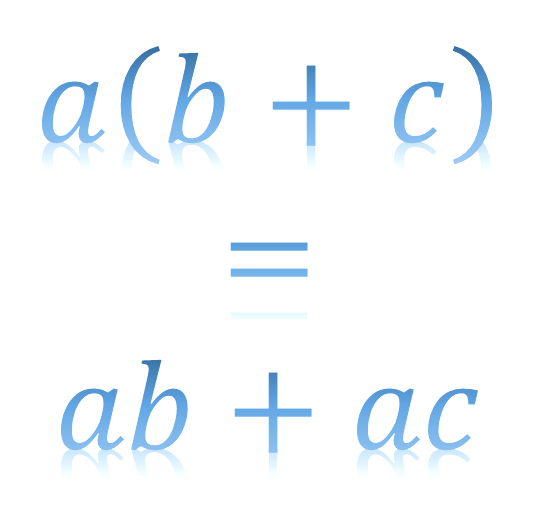
Brackets are commonly used to express mathematical formulae. In order to manipulate expressions containing brackets it is necessary to remove them first. This module discusses how to remove brackets.
Hi, I’m Martin Lindsay from the Study and Learning Centre at RMIT University. This is a short movie on removing brackets in algebra.
The law that allows us to expand expressions with brackets in maths is called the distributive law. For instance, A brackets B plus C, is the same as A times B plus A times C, you’re multiplying the term outside the brackets by the term inside the brackets, an alternate way of writing A times brackets B plus C, same thing, A times B plus A times C.
Before we get into some of the examples just recall some of our work we’ve done in the past, multiplying positive and negative numbers. Remember if the signs are the same, plus plus or minus minus the answer is positive, if the signs are different, plus and minus, then the answer is negative.
So let’s use this law and multiply out this particular expression just with numbers; two times brackets three plus five, so we’re going two times three plus two times five, two times three is six, two times five is ten, answer is 16. Let’s look at another example but here we’re using algebra; three brackets X plus two, we use the same law again, three times X plus three times two, which is three X plus six, notice we can’t add three X to six because the terms are different. Similarly with negative signs, minus five brackets M plus four gives us minus five times M plus minus five times four, which is minus five M minus 20, the terms are different so they must be left alone. And finally, with two negative signs, so be careful here, minus two brackets P minus seven is minus two times P plus minus two times minus seven, which is minus two P plus 14.
Let’s now move on with two sets of brackets, four brackets M minus three plus two brackets M plus one. We use the same ideas as before giving us four M minus 12 plus two M plus two, collect the like terms and we’ve got six M minus 10. Similarly, two sets of brackets but this time we have to be really careful because there’s a negative sign. Minus six X brackets two X plus three minus three X brackets X minus three gives us minus 12 X squared minus 18 X minus 3 X squared and there it is we’ve got plus 9 X at the end, two negatives give us a positive, collecting up the like terms we’ve got minus 15 X squared minus 9 X.
Now let’s looked at two sets of brackets that are placed side by side, in other words we’re multiplying the first set of brackets by the second set of brackets. And if you look at the example in blue the idea is to multiply the first term in the first set of brackets by the second set of brackets and the second term in the first set of brackets by the second set of brackets, in other words X multiplied by X plus three plus two multiplied by X plus three. If we expand these brackets further we have X squared plus three X plus two X plus six and collecting the like terms gives us an answer of A squared plus five X plus six.
Here are two more examples that have been written out for you. The one in blue at the top, notice there’s a negative sign so be careful here with the negative signs, giving us an answer of M squared minus M minus 20 and the example in red there are two negative signs here, so be doubly careful when multiplying out these sets of brackets, giving us an answer of Q squared minus nine Q plus 18.
Now try some questions for yourself. The answers to these problems are on the next slide. Thanks for watching this short movie.
The Distributive Law
In what follow we will write \(a\left(b+c\right)\) which means \(a\times\left(b+c\right)\). That is the \(a\) multiplies the bracket. We usually don’t include the times sign \(\left(\times\right)\).
The distributive law says that \[\begin{align*} a\left(b+c\right) & =ab+ac. \end{align*}\] In words, the \(a\) outside the bracket multiplies everything inside the bracket.
For example, \[\begin{align*} 2\left(3+5\right) & =2\times3+2\times5. \end{align*}\]
Removing the brackets is called expansion.
Examples
Expand \(3\left(x+2\right)\). We have \[\begin{align*} 3\left(x+2\right) & =3\times x+3\times2\\ & =3x+6. \end{align*}\]
Expand \(-5\left(m+4\right).\) We have \[\begin{align*} -5\left(m+4\right) & =\left(-5\right)\times m+\left(-5\right)\times4\\ & =-5m-20. \end{align*}\] Usually we omit the first step shown above and expand directly as shown in the following examples.
Expand \(-2\left(p-7\right).\) We have \[\begin{align*} -2\left(p-7\right) & =-2p+14. \end{align*}\]
Expand \(e\left(e+2\right).\) We have \[\begin{align*} e\left(e+2\right) & =e^{2}+2e. \end{align*}\]
Expand \(-\left(4p-3\right).\) We have \[\begin{align*} -\left(4p-3\right) & =-4p+3. \end{align*}\]
Expand and simplify \(4\left(x-3\right)+2\left(x+1\right).\) We have \[\begin{align*} 4\left(x-3\right)+2\left(x+1\right) & =4x-12+2x+2\\ & =6x-10. \end{align*}\]
Expand and simplify \(6k\left(2k+3\right)-3k\left(k-3\right).\) We have \[\begin{align*} 6k\left(2k+3\right)-3k\left(k-3\right) & =12k^{2}+18k-3k^{2}+9k\\ & =9k^{2}+27k. \end{align*}\] Now do some practice. See Exercise \(1\).
Binomial Products
A binomial product is something like \(\left(m+2\right)\left(m+3\right).\) It is the product of two binomial terms.1 A binomial term is an expression involving two terms. Examples are: \(a+3\), \(1+c,\) \(a+b,\) and \(\left(3x+2y\right)\).
To expand the two brackets, multiply each term in the first bracket by each term in the second bracket. Then simplify if possible. For example: \[\begin{align*} \left(m+2\right)\left(m+3\right) & =m\left(m+3\right)+2\left(m+3\right)\\ & =m^{2}+3m+2m+6\\ & =m^{2}+5m+6. \end{align*}\] Symbolically we can write: \[\begin{align*} \left(a+b\right)\left(c+d\right) & =ac+ad+bc+bd. \end{align*}\]
Two Important Cases
Special cases arise when the binomial terms are the same. That is \(\left(a+b\right)\left(a+b\right)=\left(a+b\right)^{2}\) or \(\left(a-b\right)\left(a-b\right)=\left(a-b\right)^{2}\).
We have \[\begin{align*} \left(a+b\right)^{2} & =\left(a+b\right)\left(a+b\right)\\ & =a^{2}+ab+ba+b^{2}\\ & =a^{2}+2ab+b^{2} & \left(1\right) \end{align*}\] and \[\begin{align*} \left(a-b\right)^{2} & =\left(a-b\right)\left(a-b\right)\\ & =a^{2}-ab-ba+b^{2}\\ & =a^{2}-2ab+b^{2}. & \left(2\right) \end{align*}\] These occur often in mathematics and you should commit them to memory.
Examples
- Expand \(\left(2f+3\right)\left(g+5h\right).\) We have \[\begin{align*} \left(2f+3\right)\left(g+5h\right) & =2fg+\left(2f\right)\left(5h\right)+3g+15h\\ & =2fg+10fh+3g+15h. \end{align*}\] In this case not further simplification is possible.
- Expand \(\left(p-2\right)\left(p-7\right).\) We have \[\begin{align*} \left(p-2\right)\left(p-7\right) & =p^{2}-7p-2p+14\\ & =p^{2}-9p+14 \end{align*}\]
- Expand \(\left(2w+3\right)\left(w-4\right).\) We have \[\begin{align*} \left(2w+3\right)\left(w-4\right) & =2w^{2}-8w+3w-12\\ & =2w^{2}-5w-12 \end{align*}\]
- Expand \(\left(4r-3s\right)^{2}.\) We have \[\begin{align*} \left(4r-3s\right)^{2} & =\left(4r-3s\right)\left(4r-3s\right)\\ & =16r^{2}-12rs-12sr+9s^{2}\\ & =16r^{2}-24rs+9s^{2} \end{align*}\] This can be done faster if you remember eqn (2) above: \[\begin{align*} \left(4r-3s\right)^{2} & =\left(4r\right)^{2}-2\left(4r\right)\left(3s\right)+\left(-3s\right)^{2}\\ & =16r^{2}-24rs+9s^{2} \end{align*}\] For some practice, please try out Exercise 2.
Exercise 1
- Remove the brackets:
\[\begin{array}{lll} a)\;2\left(x-5\right) & b)\;3\left(6-b\right) & c)\;\left(b+5\right)c\\ d)\;2x\left(2a+3b\right) & e)\;-6\left(p-2q+4\right) & f)\;3y\left(yz-2y+1\right) \end{array}\]
- Expand and simplify:
\[\begin{array}{lll} a)\;3\left(x+1\right)+2\left(x+2\right) & b)\;2\left(p-1\right)-\left(p-3\right) & c)\;2\left(4m-3\right)-5\left(9-2m\right)\\ d)\;2w\left(3w+1\right)+3w\left(2w-5\right) & e)\;2a\left(a-1\right)-a\left(a-3\right) & f)\;5j\left(3j+2\right)-2j\left(4j-1\right)\\ g)\;3q\left(5q+4\right)+6\left(8-3q\right) & h)\;2r\left(3r-1\right)-3r\left(3+2r\right) \end{array}\]
- Expand the following expressions and simplify where possible remembering the correct order of operations.
\[\begin{array}{lll} a)\;4\left(2m-3\right)+8 & b)\;9-3\left(4b+3\right) & c)\;1-4\left(x-1\right)\\ d)\;4-\left(5-2x\right) & e)\;8m-3\left(1-2m\right)+6 & f)\;9c\left(4-c\right)+2\left(c-7\right) \end{array}\]
\[\begin{array}{ccllccc} 1. & a)\;2x-10 & b)\;18-3b & c)\;bc+5c & d)\;4ax+6bx & e)\;-6p+12q-24 & f)\;3y^{2}z-6y^{2}+3y\end{array}\]
\[\begin{array}{cclllc} 2. & a)\;5x+7 & b)\;p+1 & c)\;18m-51 & d)\;12w^{2}-13w\\ & e)\;a^{2+a} & f)\;7j^{2}+12j & g)15q^{2}-6q+48 & h)\;-11r \end{array}\]
\[\begin{array}{llllllc} 3. & a)\;8m-4 & b)\;-12b & c)\;5-4x & d)\;-1+2x & e)\;14m+3 & f)\;38c-9c^{2}-14\end{array}\]
Exercise 2
- Expand the following binomial products:
\[\begin{array}{lll} a)\;\left(x+5\right)\left(x+3\right) & b)\;\left(u-5\right)\left(u+3\right) & c)\;\left(k+6\right)\left(j+1\right)\\ d)\;\left(y+2\right)\left(y-2\right) & e)\;\left(e-7\right)\left(e-8\right) & f)\;\left(t-3\right)\left(5-t\right)\\ g)\;\left(3q+2\right)\left(q+1\right) & h)\;\left(8a+5\right)\left(a-3\right) & i)\;\left(2c-d\right)\left(3c+2d\right)\\ j)\;\left(3a-2b\right)\left(3a+2b\right) \end{array}\]
- Remove the brackets:
\[\begin{array}{lll} a)\;\left(d+3\right)^{2} & b)\;\left(x-2\right)^{2} & c)\;\left(3v+2\right)^{2}\\ d)\;\left(y-3z\right)^{2} & e)\;\left(3-2q\right)^{2} & f)\;\left(4f-3gh\right)^{2} \end{array}\]
\[\begin{array}{lcllll} 1. & a)\;x^{2}+8x+15 & b)\;u^{2}-2u-15 & c)\;kj+6j+k+6 & d)\;y^{2}-4 & e)\;e^{2}-15e+56\\ & f)\;-t^{2}-15+8t & g)\;3q^{2}+5q+2 & h)\;8a^{2}-19a-15 & i)\;6c^{2}+cd-2d^{2} & j)\;9a^{2}-4b^{2} \end{array}\]
\[\begin{array}{llllll} 2. & a)\;d^{2}+6d+9 & b)\;x^{2}-4x+4 & c)\;9v^{2}+12v+4 & d)\;y^{2}-6yz+9z^{2} & e)\;9-12q+4q^{2}\\ & f)\;16f^{2}-24fgh+9g^{2}h^{2} \end{array}\]
