T7 Trigonometric equations
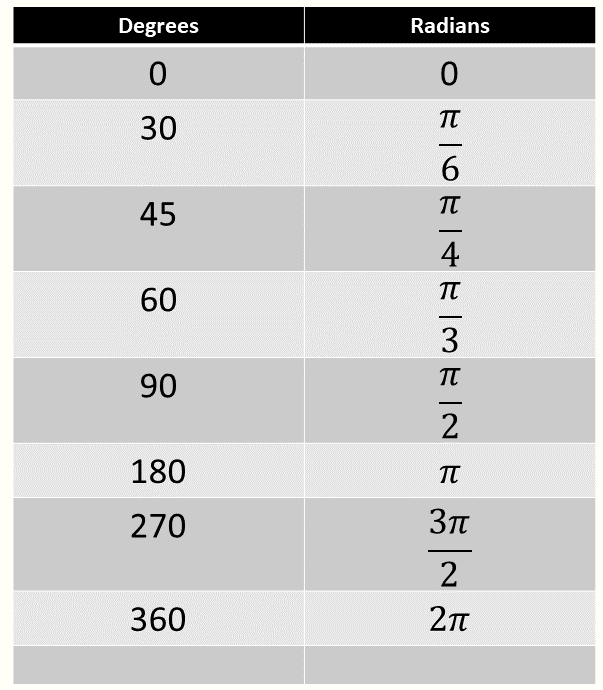
If you know the value of a trigonometric function, how do I find all the possible angles that satisfy this expression? The calculator may only give you one answer to an inverse trig question between 0 and 90 degrees (say InvCos = 40°). The unit circle can help you visualise the many different solutions for finding your angle α.
This module describes how to solve trigonometric equations over a prescribed domain. An example of such an equation is: Solve \[\begin{align*} \cos\theta & =0.5 \end{align*}\] if \(-\pi\leq\theta\leq3\pi\).
Solving these types of problem is easier if you can identify the values of trigonometric functions on a unit circle as shown in the example below. You also need to understand angles in degrees and radians.
Example 1
Given that \(\sin\theta=0.3,\) find all values of \(\theta\) in the domain \(\left\{ \theta:0^{\circ}\leq\theta\leq360^{\circ}\right\} .\)
Solution:
Draw a picture showing the possible positive values for \(\theta\) as shown below:
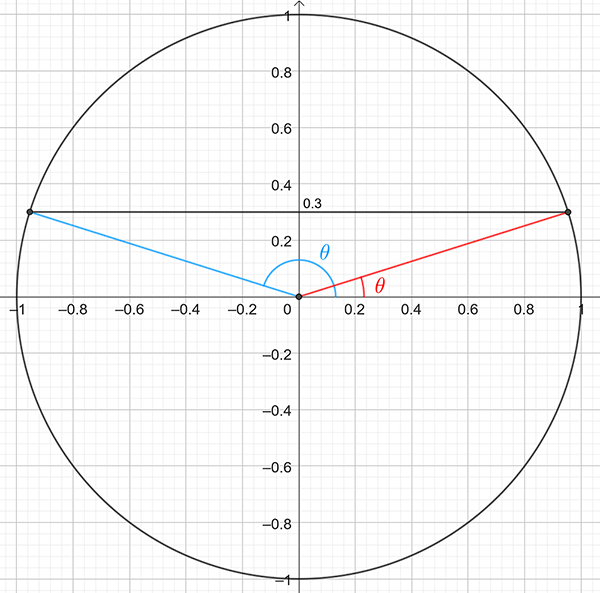
There are at least two solutions shown in red and blue. We have \(\theta_{r}\) (in red) which is given by \[\begin{align*} \theta_{r} & =\sin^{-1}\left(0.3\right)\\ & =17.46^{\circ}.\text{ (from calculator)} \end{align*}\] The other angle \(\theta_{b}\) (in blue) may be found by symmetry: \[\begin{align*} \theta_{b} & =180^{\circ}-\theta_{r}\\ & =180^{\circ}-17.46^{\circ}\\ & =162.54^{\circ}. \end{align*}\] Hence the solutions are \(\theta=17.46^{\circ},\,162.54^{\circ}.\)
Example 2
Given that \(\sin\theta=0.3,\) find all values of \(\theta\) such that \(0^{\circ}\leq\theta\leq500^{\circ}.\)
Solution:
Note that this is the same problem as in Example 1 except that the domain in which we are looking for solutions has been extended to \(500^{\circ}.\)
Draw a picture showing the possible positive values for \(\theta\) as shown below:

From Example 1 we know \(\theta=17.46^{\circ}\)or \(162.54^{\circ}.\) If we add \(360^{\circ}\) to each of these, they will still satisfy \(\sin\theta=0.3.\) The question is, are they in the domain of interest?
Adding \(360^{\circ}\) to the solution \(\theta=17.46^{\circ}\) found in Example 1 gives \[\begin{align*} \theta & =17.46^{\circ}+360^{\circ}\\ & =377.46^{\circ} \end{align*}\] which is less than \(500^{\circ}\) and so a solution to Example 2. Adding \(360^{\circ}\) to the other solution to Example \(1\) gives \[\begin{align*} \theta & =162.54^{\circ}+360^{\circ}\\ & =522.54^{\circ} \end{align*}\] which is bigger than \(500^{\circ}\) and so not a solution to Example 2.
Hence the solutions are \(\theta=17.46^{\circ},\,162.54^{\circ}\) and \(377.46^{\circ}.\)
Example 3
Solve \(\cos\alpha=0.5\) over the domain \(\left\{ \alpha:0\leq\alpha\leq2\pi\right\} .\)
Solution:
Draw a picture showing the possible positive values for \(\alpha\) as shown below:
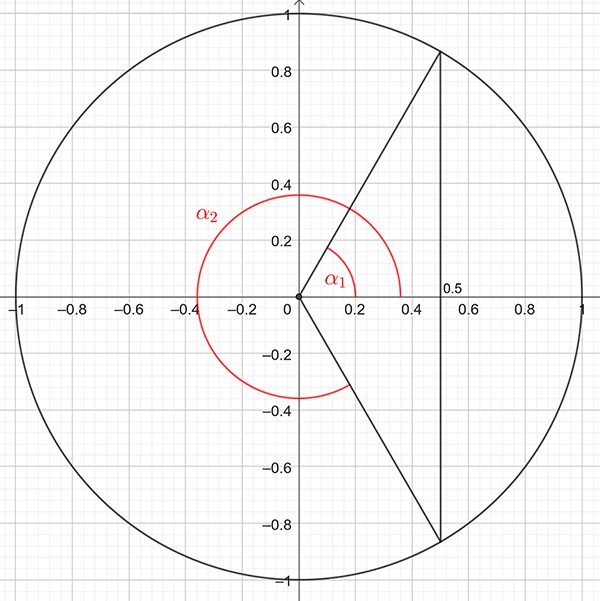
Referring to the figure, \[\begin{align*} \alpha_{1} & =\cos^{-1}\left(0.5\right)\\ & =\frac{\pi}{3}\ (\text{from calculator)} \end{align*}\] and from symmetry of the unit circle, \[\begin{align*} \alpha_{2} & =2\pi-\alpha_{1}\\ & =2\pi-\frac{\pi}{3}\\ & =\frac{5\pi}{3}. \end{align*}\] Hence the solution is \(\alpha=\pi/3\) and \(5\pi/3.\)
Example 4
Solve \(\cos\alpha=0.5\) over the domain \(\left\{ \alpha:-2\pi\leq\alpha\leq2\pi\right\} .\)
Solution:
Note this is the same problem as in Example 3 but the domain has been extended.
Draw a picture showing the possible positive and negative values for \(\alpha\) as shown below:
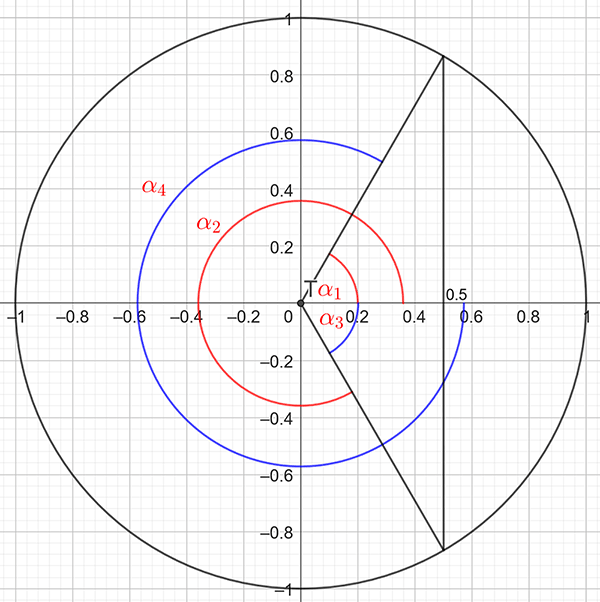
The two positive angles (shown in red) are the same as those in Example 3, namely \[\begin{align*} \alpha_{1} & =\frac{\pi}{3}\\ \alpha_{2} & =\frac{5\pi}{3}. \end{align*}\] The negative angles (shown in blue) are \(\alpha_{3}\) and \(\alpha_{4}.\) Using the results from Example 3 and symmetry we have \[\begin{align*} \alpha_{3} & =-\alpha_{1}\\ & =-\frac{\pi}{3} \end{align*}\] and \[\begin{align*} \alpha_{4} & =-\left(2\pi-\alpha_{1}\right)\\ & =\alpha_{1}-2\pi\\ & =\frac{\pi}{3}-2\pi\\ & =-\frac{5\pi}{3}. \end{align*}\] Hence the solution is \(\alpha=-\frac{5\pi}{3},\,-\frac{\pi}{3},\,\frac{\pi}{3},\,\frac{5\pi}{3}.\)
Example 5
Solve \(\tan\left(2x\right)=-3\) over the domain \(\left\{ x:-90^{\circ}\leq x\leq180^{\circ}\right\} .\)
Solution:
Since the variable is \(2x,\) we have to redefine the domain to \(\left\{ 2x:-180^{\circ}\leq2x\leq360^{\circ}\right\} .\)
Draw a picture showing the possible positive and negative values for \(2x\) as shown below:
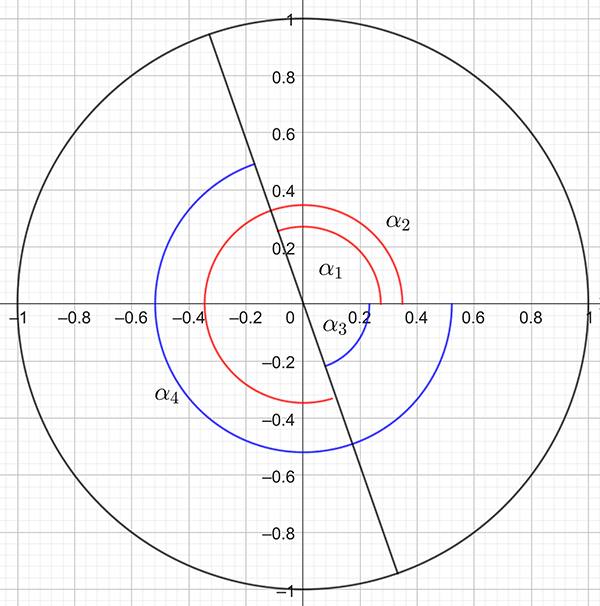
There are two positive angles \(\alpha_{1},\,\alpha_{2}\) (shown in red) and two negative angles \(\alpha_{3,}\,\alpha_{4}\) (shown in blue) that may lie within \(-180^{\circ}\leq2x\leq360^{\circ}.\)
We have \[\begin{align*} \tan\left(2x\right) & =-3\\ 2x & =\tan^{-1}\left(-3\right)\\ & =-71.57^{\circ}\ \text{(from calculator).} \end{align*}\] Referring to the figure, we see that \[\begin{align*} \alpha_{3} & =-71.57^{\circ} \end{align*}\] and \[\begin{align*} \alpha_{4} & =\alpha_{3}-180^{\circ}\\ & =-71.57^{\circ}-180^{\circ}\\ & =-251.57^{\circ}. \end{align*}\] Note that this is outside of the domain for \(2x\) and so is rejected. That is we discard \(\alpha_{4}.\)
Using the symmetry of the unit circle, we have \[\begin{align*} \alpha_{1} & =360^{\circ}+\alpha_{4}\\ & =360^{\circ}-251.57^{\circ}\\ & =108.43^{\circ} \end{align*}\] and using the figure, \[\begin{align*} \alpha_{2} & =\alpha_{1}+180^{\circ}\\ & =108.43^{\circ}+180^{\circ}\\ & =288.43^{\circ}. \end{align*}\] Hence \[\begin{align*} 2x & =\alpha_{3},\ \alpha_{1},\ \alpha_{2}\\ & =-71.57^{\circ},\ 108.43^{\circ},\ 288.43^{\circ} \end{align*}\] and the solution is \[\begin{align*} x & =-35.79^{\circ},\ 54.22^{\circ},\ 144.22^{\circ}. \end{align*}\]
Exercises
Solve the following equations:
\(\text{a) If $\sin\phi=0.25$ find $\phi$ for $0^{\circ}\leq\phi\leq180^{\circ}$ .}\)
\(\text{b) If $\tan\phi=0.8$ find }\phi\) for \(0^{\circ}\leq\phi\leq360^{\circ}\).
\(\text{c) If $\cos\phi=0.4$ find $\phi\ \text{for $0^{\circ}\leq\phi\leq360^{\circ}.$ }$ }\)
\(\text{d) If $\cos\phi=-0.4\ \text{find $\phi\text{ for $-180^{\circ}\leq\phi\leq360^{\circ}.$ }$ }$ }\)
\(\text{e) If $\tan\phi=-1.5\ \text{find $\phi\ \text{for $-180^{\circ}\leq\phi\leq360^{\circ}.$ }$ }$ }\)
\(\text{f) If $\cos\phi=-0.3\ \text{find $\phi$ for $0^{\circ}\leq$ $\phi\leq360^{\circ}.$ }$ }\)
All answers are in degrees.
\(\text{a) $14.5^{\circ},\,165.5^{\circ}$ $\qquad\text{b) $38.7^{\circ},\,218.7^{\circ}\qquad\text{c) $66.4^{\circ},\,293.6^{\circ}$ }$ }$ }\)
\(\text{d) $-113.6^{\circ},\,113.6^{\circ},\,246.4^{\circ}\qquad\text{e) $-56.3^{\circ},\,123.7^{\circ},\,303.7^{\circ}\qquad\text{f) $107.5^{\circ},\,252.5^{\circ}.$ }$ }$ }\)
Download this page, T7 Trigonometric equations (PDF 743KB)
What's next... T8 (F10) Graphs of sine and cosine functions
