D5 The chain rule
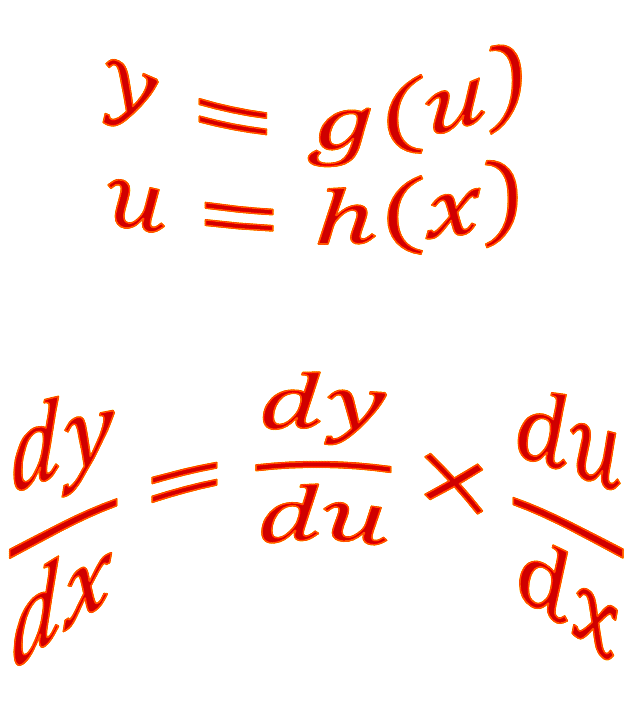
How do you differentiate a larger function that has components that are smaller functions?
This module will show you how to package these functions and work them out separately, before plugging them into the Chain Rule formula.
The derivatives of functions such as \(y=\sin\left(x^{3}\right)\)and \(f(x)=\left(x^{2}-1\right)^{4}\) can be found using the chain rule.
Hi, this is Martin Lindsay from the Study and Learning Centre at RMIT University. This is a short calculus movie on the chain rule. The chain rule is used to differentiate a function which is the composition of two simpler functions, in other words if Y equals G U where U equals H X then D Y D X is D Y D U times D U D X.
Let’s differentiate this function; Y equals two X minus one or to the power of four. So we let U equals two X minus one, then Y equals U to the power of four, differentiating, D U D X equals two, D Y D U equals four U cubed, substituting into the chain rule we have four U cubed times two which gives us eight U cubed and substituting back for U we get an answer of eight brackets two X minus one or to the power of three.
Let’s look at a trig function; Y equals sign to the five X, so we let U equal five X giving us Y equal sign U, differentiating D U D X is five, D Y D U is cos of U and substituting into the chain rule we get cos U times five which is five cos of five X, again substituting back for U which is, in this case, is five X.
Let’s look at a more complicated function here. We have Y equals one over the cubed root of 5 T square plus two T plus one, notice first of all that we’ve changed the variable here, instead of D Y D S we’ve got D Y D T, it doesn’t matter we can still use the same process as before. First of all always changed cube roots, square roots and so on into index form to make the differentiation easier, using our substitution, differentiating D U D T, D Y D U, and now using the chain rule which in this case D Y D T equals D Y D U times D U D T and substituting we get that, which gives us, after simplifying that answer.
Here’s another trig function but note first of all that instead of Y and D Y D X we’ve got F X and F dash X. First of all recall that if Y equals cos cubed X that’s the same as cos of X or to the power of three. Using our substitution Y equals U cubed where U equals cos of X, now we differentiate, D Y D U equals three U squared, D U D X equals minus sign of X. Notice I’ve moved back from F X and F dash X to Y and D Y D X. Now let’s do the chain rule, substituting and substituting back for U we get an answer of minus three sign X cos squared X. Note that the chain rule can be extended to three or more functions. Up to now we’ve been looking at two functions.
Here’s an example of a three function problem; Y equals log of four X or to the power of three, the three here are Y equals U cubed, U equals log of V and V is equal to four X, differentiating the three, D Y D U is three U squared, D U D V is one over V and D V D X is four, substituting for D Y D U, D U D V and D V D X we get the following, and substituting back we get an answer of three over X brackets log of four X or to the power of two after simplifying.
Now try some problems for yourself. The answers to these questions are on the next slide. Thanks for watching this short movie.
The Chain Rule for Differentiation
If \(y\) = g\(\left(u\right)\) where \(u\) = h\(\left(x\right)\), then \[ \frac{dy}{dx}=\frac{dy}{du}\times\frac{du}{dx}. \]
Examples
- Differentiate \(y=(2x-1)^{4}\)
Solution:
Let \(u=2x-1\), then \(y=u^{4}\) and \[\begin{align*} \frac{du}{dx} & =2\\ \frac{dy}{du} & =4u^{3}. \end{align*}\] Hence, using the chain rule, \[\begin{align*} \frac{dy}{dx} & =\frac{dy}{du}\times\frac{du}{dx}\\ & =4u^{3}\times2\\ & =8u^{3}\\ & =8\left(2x-1\right)^{3}. \end{align*}\] Note the last step where we convert from \(u\) back to \(x\). Don’t forget to do this.
- Differentiate \(y=\sin\left(5x\right).\)
Solution:
Let \(u=5x\), then \(y=\sin\left(u\right)\) and \[\begin{align*} \frac{du}{dx} & =5\\ \frac{dy}{du} & =\cos\left(u\right). \end{align*}\] Hence, using the chain rule, \[\begin{align*} \frac{dy}{dx} & =\frac{dy}{du}\times\frac{du}{dx}\\ & =\cos\left(u\right)\times5\\ & =5\cos\left(5x\right). \end{align*}\]
- Find the derivative of \[\begin{align*} y & =\frac{1}{\sqrt[3]{5t^{2}+2t+1}} \end{align*}\] with respect to \(t.\)
Solution:
First convert to index form then \[\begin{align*} y & =\left(5t^{2}+2t+1\right)^{1/3}. \end{align*}\] Let \(u=5t^{2}+2t+1\), then \(y=u^{-1/3}\) and \[\begin{align*} \frac{du}{dt} & =10t+2\\ \frac{dy}{du} & =-\frac{1}{3}u^{-4/3}. \end{align*}\] Hence, using the chain rule, \[\begin{align*} \frac{dy}{dt} & =\frac{dy}{du}\times\frac{du}{dt}\\ & =-\frac{1}{3}u^{-4/3}\times\left(10t+2\right)\\ & =-\frac{1}{3}\left(10t+2\right)\left(5t^{2}+2t+1\right)^{-4/3}. \end{align*}\]
- If \(f\left(x\right)=\cos^{3}\left(x\right)\) find \(f'\left(x\right).\)
Solution:
Let \(y=f\left(x\right)\) and \(u=\cos\left(x\right)\) then \(y=f\left(x\right)=u^{3}\) and \[\begin{align*} \frac{dy}{du} & =3u^{2}\\ \frac{du}{dx} & =-\sin\left(x\right). \end{align*}\] Hence, using the chain rule, \[\begin{align*} f'\left(x\right) & =\frac{dy}{dx}\\ & =\frac{dy}{du}\times\frac{du}{dx}\\ & =3u^{2}\times\left(-\sin\left(x\right)\right)\\ & =-3\sin\left(x\right)\cos^{2}\left(x\right). \end{align*}\]
- Differentiate \(y=\left(\log_{e}\left[4x\right]\right)^{3}\).
Solution:
In this case the \(y\) is composed of three functions.
Let \(v=4x,\) \(u=\log_{e}\left(v\right)\) and \(y=u^{3}\) then \[\begin{align*} \frac{dy}{du} & =3u^{2}\\ \frac{du}{dv} & =\frac{1}{v}\\ \frac{dv}{dx} & =4. \end{align*}\] Using the chain rule, \[\begin{align*} \frac{dy}{dt} & =\frac{dy}{du}\times\frac{du}{dv}\times\frac{dv}{dx}\\ & =3u^{2}\times\frac{1}{v}\times4\\ & =12\left(\log_{e}\left(v\right)\right)^{2}\times\frac{1}{v}\\ & =12\left(\log_{e}\left(4x\right)\right)^{2}\times\frac{1}{4x}\\ & =\frac{3}{x}\left(\log_{e}\left(4x\right)\right)^{2}. \end{align*}\]
Exercise
Find the derivatives of the following functions
\(y=\tan\left(3x\right)\)
\(f(x)=\log_{e}\left(\frac{x}{2}\right)\)
\(y=\sin\left(\frac{\pi}{4}-2x\right)\)
\(y=\cos^{2}x\)
\(f(x)=e^{\sin\left(x\right)}\)
\(y=\cos^{2}\left(10x\right)\)
\(y'=3\sec^{2}\left(3x\right)\)
\(f'(x)=\frac{1}{x}\)
\(y'=-2\cos\left(\frac{\pi}{4}-2x\right)\)
\(y'=-2\sin\left(x\right)\cos\left(x\right)\)
\(f'(x)=e^{\sin x}\) \(\cos x\)
\(y'=-20\sin\left(10x\right)\cos\left(10x\right)\)
Download this page, D5 The chain rule (PDF 149KB)
What's next... D6 The product rule
