D14 Higher Order Derivatives
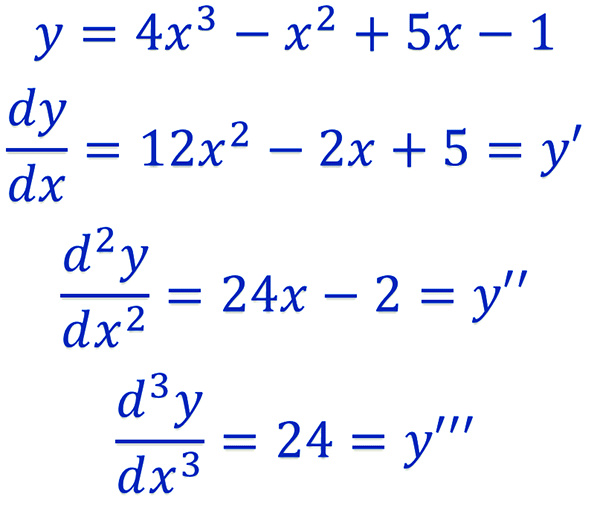
Higher derivatives are used in many mathematical, scientific and engineering subjects.
Consider a function \(y=f(x)=4x^{3}-6x^{2}+7\). If we differentiate this function we obtain \(f^{\prime}\left(x\right)=12x^{2}-12x\). This is the first derivative of the function \(y=f\left(x\right)\). It is possible to find second, third and subsequent derivatives by continuing to differentiate and these are called higher order derivatives:
\[\begin{align*} f^{\prime\prime}\left(x\right) & =24x-12\text{ $\left(\text{second derivative}\right)$ }\\ f^{\prime\prime\prime}\left(x\right) & =24\text{ $\left(\text{third derivative}\right)$ }\\ f^{\prime\prime\prime\prime}\left(x\right) & =0\text{ $\left(\text{fourth derivative}\right)$ } \end{align*}\] and all subsequent derivatives will also be zero.
Other Notations
Recall that for the first derivative we may write \(f^{\prime}\left(x\right)=\frac{dy}{dx}\). Similarly for higher order derivatives \(f^{\prime\prime}\left(x\right)=\frac{d^{2}y}{dx^{2}},\,f^{\prime\prime\prime}\left(x\right)=\frac{d^{3}y}{dx^{3}}\) and so on. We may also write\(f^{\prime\prime}\left(x\right)=f^{\left(2\right)}\left(x\right),\,f^{\prime\prime\prime}\left(x\right)=f^{\left(3\right)}\left(x\right)\) etc. and where there is no confusion \(y^{\prime},y^{\prime\prime},y^{\prime\prime\prime},\ldots\) can be used to represent first, second, third and other higher order derivatives. Note that sometimes roman numerals are used and so \(f^{\prime\prime\prime\prime}\left(x\right)=f^{\left(iv\right)}\left(x\right).\)
Applications
Higher derivatives are used in many mathematical, scientific and engineering subjects. Some examples follow.
Acceleration:
Velocity \(v\left(t\right)\) is the first derivative of the displacement function \(s\left(t\right)\) with respect to time . \[\begin{align*} v & =\frac{ds}{dt} \end{align*}\] And acceleration is the rate of change or first derivative of the velocity function. It follows that acceleration \(a\) is the second derivative of the displacement function: \[\begin{align*} a & =\frac{d}{dt}\left(\frac{ds}{dt}\right)\\ & =\frac{d^{2}s}{dt^{2}}. \end{align*}\]
Beam deflection:
The equation which describes the deflection \(w\) of a uniform static beam in engineering makes use of the fourth derivative:
\[ EI\frac{d^{4}w}{dx^{4}}=q(x). \]
Points of inflection:
When graphing a function the second derivative is the rate of change of the derivative function. It describes the concavity of the curve and indicates whether the slope of the function is increasing or decreasing.
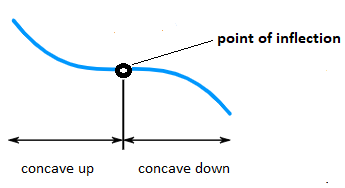
- If the graph of the function is concave upward the second derivative is positive - slope increasing.
- If the graph of the function is concave downward the second derivative is negative - slope decreasing.
- At a point of inflection, where the curve changes concavity, the second derivative is zero.
Example 1
Find the \(4^{th}\text{ derivative of $f\left(x\right)=\sin\left(2x\right).$ }\)
Solution:
\[\begin{align*} f^{\prime}\left(x\right) & =2\cos(2x)\\ f^{\prime\prime}\left(x\right) & =-4\sin(2x)\\ f^{\left(3\right)}(x) & =-8\cos(2x)\\ f^{\left(4\right)}(x) & =16\sin(2x). \end{align*}\] The fourth derivative of \(f\left(x\right)=\sin\left(2x\right)\) is \(f^{\left(4\right)}(x)=16\sin(2x).\)
Example 2
If \(f\left(x\right)=3x^{4}-5x^{2}+7,\) find \(f^{\prime\prime}\left(x\right).\)
Solution:
\[\begin{align*} f^{\prime}\left(x\right) & =12x^{3}-10x\\ f^{\prime\prime}\left(x\right) & =36x^{2}-10. \end{align*}\]
Example 3
Find \(\frac{d^{2}y}{dt^{2}}\) if \(y=\ln\left(1+t^{4}\right)\)
Solution:
Using the chain rule,
\[\begin{align*} \frac{dy}{dt} & =\frac{1}{1+t^{4}}4t^{3}\\ & =\frac{4t^{3}}{1+t^{4}}. \end{align*}\] Now applying the quotient rule,
\[\begin{align*} \frac{d^{2}y}{dt^{2}} & =\frac{\left(1+t^{4}\right)\cdot12t^{2}-4t^{3}\cdot4t^{3}}{\left(1+t^{4}\right)^{2}}\\ & =\frac{12t^{2}+12t^{6}-16t^{6}}{\left(1+t^{4}\right)^{2}}\\ & =\frac{12t^{2}-4t^{6}}{\left(1+t^{4}\right)^{2}}. \end{align*}\]
Example 4
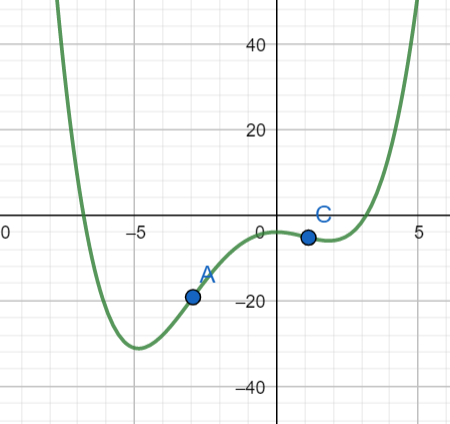
Find the \(x-\)coordinates of the points of inflection for the curve with equation: \[\begin{align*} y & =\frac{x^{4}}{12}+\frac{x^{3}}{3}-\frac{3x^{2}}{2}+3x-7. \end{align*}\]
Solution:
\[\begin{align*} y^{\prime} & =\frac{4x^{3}}{12}+\frac{3x^{2}}{3}-\frac{6x}{2}+3\\ & =\frac{x^{3}}{3}+x^{2}-3x+3\\ y^{\prime\prime} & =x^{2}+2x-3. \end{align*}\]
Points of inflection will occur where \(y^{\prime\prime}=0:\) \[\begin{align*} x^{2}+2x-3 & =0\\ (x+3)(x-1) & =0\\ x=-3,\ & x=1 \end{align*}\]
There are points of inflection at \(x=-3\) and \(x=1\) and this is confirmed by the graph of the function.
Exercises
\(1.\) Find the third derivative of \(y=x^{5}-2x^{2}+8x\) \(.\)
Answer
\(y=20x^{3}-4\).
\(2.\) If \(f\left(x\right)=e^{x^{3}}\)find \(f^{\prime\prime}\left(x\right)\)
Answer
\(f^{\prime\prime}\left(x\right)=e^{x^{3}}\left(6x+9x^{4}\right)\).
\(3.\) Given \(y=t^{4}+\frac{1}{t^{4}}\)find \(\frac{d^{3}y}{dt^{3}}\).
Answer
\(\frac{d^{3}y}{dt^{3}}=24t-\frac{120}{t^{7}}\).
\(4.\) The displacement of a particle at time \(t\) is described by the function \(s\left(t\right)=t^{2}-\cos\left(3t\right)\). What is the initial acceleration of the particle?
Answer
\(a=s^{\prime\prime}(t)=11\) when t = 0.
\(5.\) Find any points of inflection for the graph of the function \(y=\frac{x^{4}}{4}-2x^{3}+6x^{2}+x-10\).
Answer
There is a single point of inflection at \(\left(2,4\right).\)
Download this page, D14 Higher Order Derivatives (PDF 233KB)
What's next... D15 Logarithmic differentiation
