A3.1 Common factors
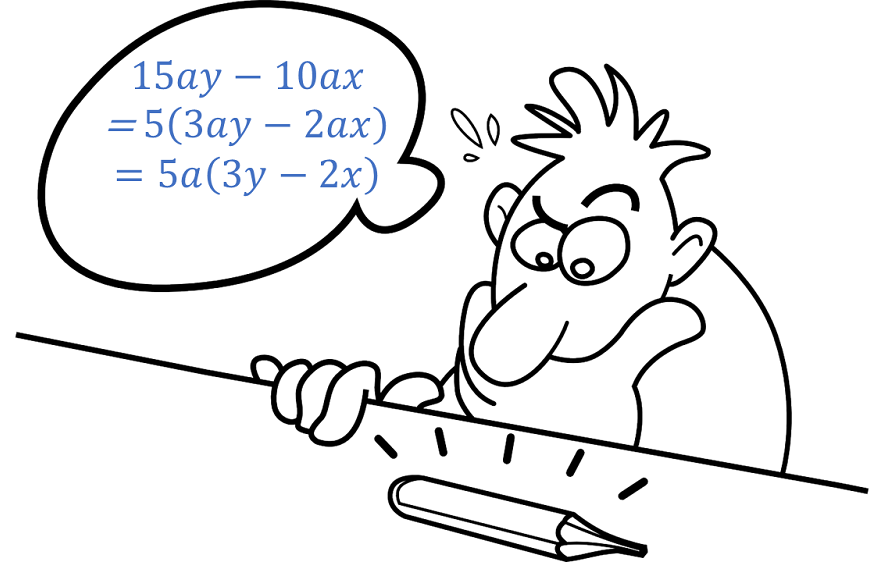
Image: Pixabay
A common factor is a number or pronumeral that is common to terms in an algebraic expression. Removing the common factors allows us to factorise algebraic expressions and write them in a simpler form. Factorisation using common factors is a basic skill in mathematics and is discussed in this module.
This module looks at using common factors to factorise mathematical expressions.
Hi, this is Martin Lindsay from the Study and Learning Centre at RMIT University. This is a short movie on finding common factors in algebra. Let’s start by recalling that expansion or removing brackets is all about multiplying all the terms inside the brackets by those outside. For instance A brackets B plus C is the same as A times B plus A times C, if A brackets two Y minus four A is equal to 10 A Y minus 20 A X.
Factorisation is the reverse of expansion or removing brackets. For example, here’s an example, 10 A Y minus 20 A X. At this stage just look at the right hand side which are the factors, five A and brackets two Y minus four X, they are the factors, so moving from right to left, multiplying five A by the brackets will give you 10 A Y minus 20 A X. Similarly the factors for this expression are three and X minus Y and multiplying those terms will give us three X minus three Y, so to factorise an algebraic expression we look for a common factor, if there is more than one common factor we multiply them to get the highest common factor, HCF, the highest common factor is then placed before the bracket and the terms inside the brackets are found by dividing each term by the highest common factor.
Let’s do some examples to explain these four important steps. Here’s an example, five Y plus 10. First of all let’s look for the common factor and here the common factor of five Y and 10 is five, in other words five will divide into five Y and five will divide into 10. In other words that’s the same as five times Y plus five times two, it’s the same as five brackets Y plus two, so note the four steps, we factorise, the common factor is five, we place the five before the brackets and what goes after that five will be the other factor, Y plus two, which is inside the brackets.
Here’s another example, but this time we’re using pro-numerals, P squared plus P. What is the common factor of P squared plus P, well it’s P, P will go into P squared and P will go into P, so that’s the same as P times P plus P times one which again is the same as P brackets P plus one. There are two factors P and P plus one, the common factor P, P is placed before the brackets, the P plus one is placed inside the brackets.
Here is a slightly more complicated one. We’re mixing numbers and pro-numerals here. What’s the common factor of two A B and 12 A, well two goes into both those terms but also A does as well so the common factor is two and A, so we call that the highest common factor here, we put the two together and call them one thing, two A, same as two A times B minus two A times six, which can be written in another way, two A brackets B minus six. So to repeat, factorising, highest common factor is two A, two A before the brackets, B minus six is placed inside the brackets, which is the other factor.
Now do some questions for yourself. The answers to these problems are on the next slide. Thanks for watching this short movie.
Expansion
Expansion of brackets (or removing brackets) in an algebraic expression is done by multiplying all the terms inside the brackets by the term(s) outside the brackets.
Examples:
\[\begin{align*} 6(7) & =42\\ 6(b+1) & =6b+6\\ 3(4x+5) & =12x+15\\ 5a(3y-2x) & =15ay-10ax \end{align*}\]
Factorisation is the Reverse of Expansion
Factors are numbers we can multiply together to get another number.
To factorise a number or algebraic expression means to write the number or expression as a product (multiplication) of numbers or expressions.
Examples:
\(42=6\times7=2\times3\times7\) has factors \(6\) and \(7\) but also has factors of \(2\) and \(3\) .
\(-2xyz\)=\(-1\times2\times x\times y\times z\) has factors \(-1\) , \(2\) , \(x\) , \(y\) , \(z\) but remember that combinations are factors such as \(-2\times xy\times z\) which means that \(-2\) , \(xy\), \(xyz\), and \(z\) are factors as well.
\(6b+6=6(b+1)=2\times3\times(b+1)\) has factors \(6\) and \((b+1)\) as well as \(2\) and \(3\), the Highest Common Factor of \(6b+6\) is \(6\) .
\(12x+15=3(4x+5)\) has factors \(3\) and \(4x+5\). The Highest Common Factor of \((12x+15)\) is \(3\).
\(15ay-10ax=5a(3y-2x)\) has factors \(5\) , \(a\) and \((3y-2x)\) , \(5a\) and \(5\left(3y-2x\right)\). The Highest Common Factor of \((3y-2x)\) is \(5a\).
\(4prs+16pr+2ps+8p=2p(2rs+8r+s+4)\) \(=2p(2r+1)(s+4)\) has factors \(2\) , \(p\) , \((2r+1)\) , (\(s+4)\) as well as \((2rx+8r+s+4)\) as well as \(2p\) .
Expansion means removing brackets
Factorisation means inserting brackets
Factorisation by Removing a Common Factor
The steps are:
- Search each term in the expression for a common factor (every term must have this factor)
- There may be several common factors. Search until you have found all of them
- If there is more than one common factor multiply them to give Highest Common Factor . (HCF)
- The HCF is placed before the bracket.
- The terms inside the bracket are found by dividing each term by the HCF.
Examples:
\[\begin{align*} 5y+10 & =5\times y+5\times2\\ & =5(y+2)\\ & common\ factor\ of\ 5 \end{align*}\]
\[\begin{align*} 3x+3y & =3\times x+3\times y\\ & =3(x+y)\\ & common\ factor\ of\ 3 \end{align*}\]
\[\begin{align*} p^{2}+p & =p\times p+p\times1\\ & =p(p+1)\\ & common\ factor\ of\ p \end{align*}\]
\[\begin{align*} 7y^{2}+7y & =7y\times y+7y\times1\\ & =7y(y+1)\\ & common\ factors\ of\ 7\ and\ y\\ & HCF=7y \end{align*}\]
\[\begin{align*} 2abc-12ac & =2a\times bc-2a\times6c\\ & =2ac\times b-2ac\times6\\ & =2ac(b-6)\\ & common\ factors\ of\ 2,\ a,\ and\ c\\ & HCF=2ac \end{align*}\]
See exercise 1.
Further Examples (Negative Factors)
\[\begin{align*} -2a-2b & =(-2)\times a+(-2)\times b\\ & =-2(a+b)\\ & common\ factor\ of\ -2 \end{align*}\]
\[\begin{align*} -3x+6xy & =(-3x)\times1-(-3x)\times2y\\ & =-3x(1-2y) & HCF=-3x\\ & =3x(-1+2y) & HCF=3x\\ & =3x(2y-1) & \textrm{} \end{align*}\]
See exercise 2
Exercise 1
Factorise the following expressions (if possible):
\[\begin{array}{llllll} a) & 3x+3y & b) & 2a-2b & c) & 8a-8b+8c\\ d) & xy-5x & e) & x^{2}-x & f) & 7x+21y\\ g) & 5m-2n & h) & c^{2}-2bc-3c & i) & 5mn-10n\\ j) & 3m^{2}-3mnp & k) & 7x+21x^{2} & l) & 12m^{2}-18mn\\ m) & 5xy-10xz & n) & 5pq-pq^{2}-3pqr & o) & 2ab^{2}c+6abc^{2}\\ p) & rst+5rst^{2}-2rs & q) & 5mn+10m-pqr & r) & 5xyz-x^{2}yz^{2}+10x\\ \end{array}\]
\[\begin{array}{llllll} a) & 3(x+y) & b) & 2\left(a-b\right) & c) & 8(a-b+c)\\ d) & x(y-5) & e) & x\left(x-1\right) & f) & 7(x+3y)\\ g) & no\ factors & h) & c(c-2b-3) & i) & 5n(m-2)\\ j) & 3m(m-np) & k) & 7x(1+3x) & l) & 6m(2m-3n)\\ m) & rs(t+5t^{2}-2) & n) & pq(5-q-3r) & o) & 2abc(b+3c)\\ p) & rs\left(t+5t^{2}-2\right) & q) & no\ factors & r) & x(5yz-xyz^{2}+10)\\ \end{array}\]
Exercise 2
Factorise the following by removing a negative factor.
\[\begin{array}{llllll} a) & -3x-6y & b) & -15xy+25xz & c) & -2xy+4xyz\\ d) & 14xyz-7xy & e) & -6xyz-15yz-3xy^{2}z & f) & 7x-21y\\ \end{array}\]
\[\begin{array}{llllll} a) & -3(x+2y) & b) & -5x(y-5z) & c) & -2xy(1-2z)\\ d) & 7xy(2z-1) & e) & -3yz(2x+5+xy) & f) & 7(x-3y)\\ \end{array}\]
Download this page, A3.1 FactorisationCommon Factors (PDF 326 KB)
What's next... Perfect squares
