S8 Binomial probability
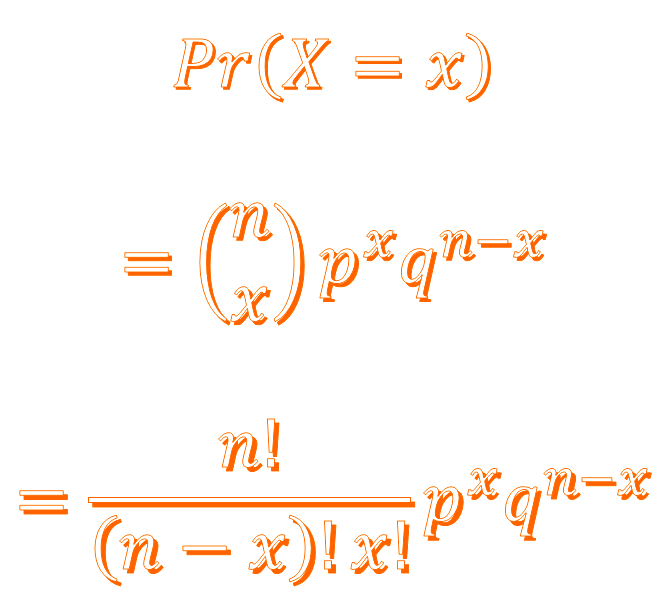
Introduction
A random variable may be described as having a binomial distribution when there are a number of repeated trials and there are only two possible outcomes on each trial.
The following are all examples of probability questions about binomial data:
- What is the probability of obtaining \(5\) heads in \(6\) tosses of a coin? Six repeated trials each with two possible outcomes: head or tail.
- What is the probability that in a randomly selected group of \(30\) people none of them will have a particular disease? \(30\) repeated “trials” each with two possible outcomes: have disease or do not have disease.
- What is the probability that in a sample of \(100\) manufactured components no more than \(2\) will be defective? \(100\) repeated trials each with two possible outcomes: defective or not defective.
Example
Suppose that in a particular family the probability that a child will have red hair is \(1/4.\)
Then, if the parents have three children:
the probability that all three will have red hair is \[\begin{align*} P(\textrm{Red and Red and Red}) & =P(R_{1}\cap R_{2}\cap R_{3})\\ & =\frac{1}{4}\times\frac{1}{4}\times\frac{1}{4}\\ & =\frac{1}{64}. \end{align*}\]
the probability that none will have red hair is \[\begin{align*} P(\overline{R}_{1}\cap\overline{R}_{2}\cap\overline{R}_{3}) & =\frac{3}{4}\times\frac{3}{4}\times\frac{3}{4}\\ & =\frac{27}{64}. \end{align*}\]
the probability that at least one child will have red hair is 1 Note: “at least one child has red hair” and “no children have red hair” are complementary events. \[\begin{align*} 1-P(\textrm{none with red hair}) & =1-P(\overline{R}_{1}\cap\overline{R}_{2}\cap\overline{R}_{3})\\ & =1\text{\textendash}\frac{3}{4}\times\frac{3}{4}\times\frac{3}{4}\\ & =1-\frac{27}{64}\\ & =\frac{37}{64}. \end{align*}\]
the probability that only the first child will have red hair is \[\begin{align*} P(R_{1}\textrm{ and }\overline{R}_{2}\textrm{ and }\overline{R}_{3}) & =\frac{1}{4}\times\frac{3}{4}\times\frac{3}{4}\\ & =\frac{9}{64}. \end{align*}\]
the probability that exactly one child will have red hair is 2 This example demonstrates that it is important to consider all the ways in which the child with red hair might be selected. \[\begin{align*} & P(R_{1}\textrm{ and }\overline{R}_{2}\textrm{ and }\overline{R}_{3})+P(\overline{R}_{1}\textrm{ and }R_{2}\textrm{ and }\overline{R}_{3})+P(\overline{R}_{1}\textrm{ and }\overline{R}_{2}\textrm{ and }R_{3})\\ & =\left(\frac{1}{4}\times\frac{3}{4}\times\frac{3}{4}\right)+\left(\frac{3}{4}\times\frac{1}{4}\times\frac{3}{4}\right)+\left(\frac{3}{4}\times\frac{3}{4}\times\frac{1}{4}\right)\\ & =3\times\left(\frac{1}{4}\right)^{1}\left(\frac{3}{4}\right)^{2}\\ & =3\times\frac{9}{64}\\ & =\frac{27}{64}. \end{align*}\]
Binomial Probability Formula
If “\(n\)” is the number of trials (for example, the number of tosses of a coin, the number of children in a family, the number of items in a sample), and “\(p\)” is the probability of the outcome of interest then the probability of “\(x\)” outcomes is given by the formula \[\begin{align*} P(X=x) & =\textrm{}^{n}C\textrm{}_{x}\times p^{x}\times\textrm{$(1-p)^{n-x}$ } & \left(1\right) \end{align*}\] where \(^{n}C_{x}\) is the number of ways of selecting \(x\) items from a popoulation of \(n\) items, without regard to order, and \[\begin{align*} ^{n}C_{x} & =\frac{n!}{x!\left(n-x\right)!}. \end{align*}\]
Example
One in every hundred items a machine produces are defective. What is the probability that in a sample of five items produced by this machine
(a) Exactly three are defective?
(b) None are defective ?
(c) At least 1 is defective?
Solution:
We have
\(n=5,\quad p=\frac{1}{100}=0.01,\quad x=3\)
Using equation \(\left(1\right)\) from above \[\begin{align*} P(X=x) & =\textrm{}^{n}C\textrm{}_{x}\times p^{x}\times\textrm{$(1-p)^{n-x}$ }\\ P(X=3) & =\textrm{}^{5}C\textrm{}_{3}\times0.01^{3}\times\textrm{$(1-0.01)^{5-3}$ }\\ & \approx0.00001. \end{align*}\] So if we obtained three defective items in a sample of \(5\) we might be suspicious of the claim that only one in a hundred is defective!
Using equation \(\left(1\right)\) from above \[\begin{align*} P(X=0) & =\textrm{}^{5}C\textrm{}_{0}\times0.01^{0}\times\textrm{$(1-0.01)^{5}$ }\\ & \approx0.95\,. \end{align*}\]
Remember “none defective” and “at least one defective” are complementary events. So
\[\begin{align*} P(X\geq1) & =1-P(X=0)\\ & =1-0.95\\ & =0.05. \end{align*}\]
Binomial Probability Distribution
A list of all possible outcomes of an event and their associated probabilities is called a probability distribution.
The probability distribution table for the event \(X\) in the example above is (to five decimal places):
| \(x\) (no. of defectives) | 0 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|---|
| \(P(X=x)\) | 0.95099 | 0.04803 | 0.00097 | 0.00001 | 0.00000 | 0.00000 |
For a binomial distribution the mean \(\mu\) or expected value and standard deviation \(\sigma,\)are found using the formulae:
\[ \mu=E(X)=np \]
and
\[ \sigma=SD(X)=\sqrt{np(1-p)} \] where \(E(X)\) is known as the expected value.
For the previous example, the expected value and standard deviation of the number of defectives in a batch of one thousand would be \[\begin{align*} \mu & =E(X)\\ & =1000\times0.01\\ & =10 \end{align*}\] and \[\begin{align*} \sigma & =\sqrt{np(1-p)}\\ & =\sqrt{1000\times0.01\times0.99}\\ & =3.15\,. \end{align*}\]
So that in a batch of \(1000\) we would expect to get \(10\) defectives and the number of defectives will deviate from this amount by an “average” of \(3.15\). We would expect most batches to have between \(7\) and \(13\) defective items.
Exercise
The probability that an archer will hit a bullseye is \(0.7\). If he is allowed ten attempts, find the probability that he
(a) hits it every time
(b) misses each time
(c) scores two bulls-eyes
(d) scores at least two bulls-eyes
(e) How many bulls-eyes would you expect him to score?
- \(0.028\)
- \(0.000006\)
- \(0.00145\)
- \(0.99986\)
- \(7\)
Download this page: S8 Binomial Probability (PDF 154KB)
What's next... S9 Normal distribution
