S7 Conditional probability
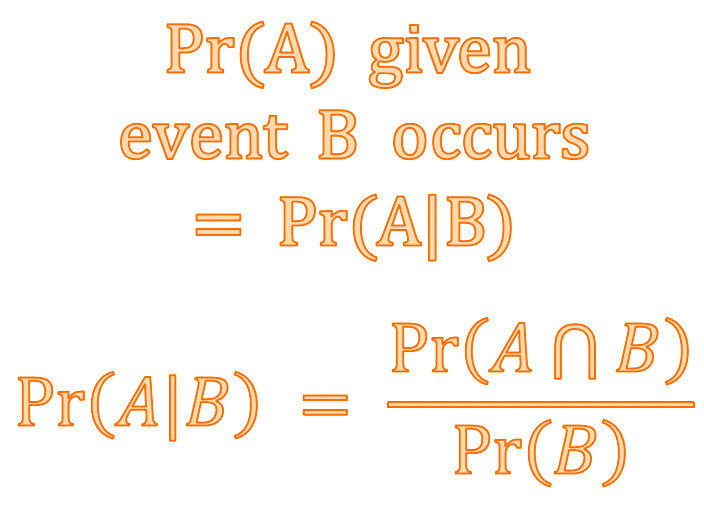
Dependent Events
Two events are dependent if the outcome or occurrence of the first affects the outcome or occurrence of the second so that the probability is changed.
Example
A card is chosen at random from a pack. If the first card chosen is the jack of diamonds and it is not replaced what is the probability that the second card is
- a diamond? 1Because the first card was the jack of diamonds and not replaced, there is one less diamond in the pack and one less card in the pack.
Pr(\(\diamondsuit\)) = \(\dfrac{12}{51}\) = \(\dfrac{4}{17}\).
- a jack?
Pr(jack) = \(\dfrac{3}{51}\) = \(\dfrac{1}{17}\)
- the queen of clubs?
Pr(Q\(\clubsuit\)) = \(\dfrac{1}{51}\)
The events J\(_{1}\) “jack of diamonds on the first draw” and D\(_{2}\) “a diamond on the second draw” are dependent when there is no replacement.
The probability of choosing a diamond on the second draw given that the jack of diamonds was chosen on the first pick is called a conditional probability.
We say “The probability of D\(_{2}\) given J\(_{1}\) is \(\dfrac{4}{17}\)” and write this as \[\begin{align*} \Pr\left(\text{D$_{2}$ |$\text{J$_{1}$ }$ }\right) & =\frac{4}{17}. \end{align*}\]
Multiplication Rule
When two events, \(A\) and \(B\), are dependent, the probability of both occurring is: \[ Pr(A\:and\:B)=Pr(A\cap B)=Pr(A)\times Pr(B|A). \]
Example
Find the probability of obtaining two jacks if two cards are drawn is succession from a pack
with replacement
without replacement.
Solution a).
If the cards are replaced then the events are independent and
\[\begin{align*} Pr(J_{1}\cap J_{2}) & =Pr(J_{1})\times Pr(J_{2})\\ & =\frac{4}{52}\times\frac{4}{52}\\ & =\frac{1}{169}. \end{align*}\]
Solution b).
If the cards are not replaced then the probability of the second draw depends on the first draw: \[\begin{align*} Pr(J_{1}\cap J_{2}) & =Pr(J_{1})\times Pr(J_{2}|J_{1})\\ & =\frac{4}{52}\times\frac{3}{51}\\ & =\frac{1}{221}. \end{align*}\]
Conditional Probability
The multiplication rule for dependent events can be rearranged to find a conditional probability: \[\begin{align*} Pr(B|A) & =\frac{Pr(A\cap B)}{Pr(A)} & \left(1\right)\\ or\\ Pr(A|B) & =\frac{Pr(A\cap B)}{Pr(B)}. & \left(2\right) \end{align*}\]
Examples
1. Find the \(Pr(A|B)\) if \(Pr(A)=0.7,Pr(B)=0.5\) and \(Pr(A\cup B)\) \(=0.8\).
Solution:
First find \(Pr(A\cap B)\). 2 We need this to use equation \(\left(2\right).\)
\[\begin{align*} Pr(A\cup B) & =Pr(A)+Pr(B)-Pr(A\cap B)\\ 0.8 & =0.7+0.5-Pr(A\cap B)\\ Pr(A\cap B) & =0.7+0.5-0.8\\ & =0.4. \end{align*}\]
and
\[\begin{align*} Pr(A|B) & =\dfrac{Pr(A\cap B)}{Pr(B)}\\ & =\dfrac{0.4}{0.5}\\ & =0.8. \end{align*}\]
2. In a class of \(15\) boys and \(12\) girls two students are to be randomly chosen to collect homework.
What is the probability that both students chosen are boys?
Solution:
We have, 3 Note that the probability of a boy on the second choice, given a boy was chosen first, is \[\begin{align*} \Pr\left(B_{2}|B_{1}\right) & =\frac{14}{26} \end{align*}\] because there is one less boy and one less student to select.
\[\begin{align*} Pr(B1\cap B2) & =Pr(B_{1})\times Pr(B2|B1)\\ & =\dfrac{15}{27}\times\dfrac{14}{26}\\ & =\dfrac{210}{702}\\ & =\dfrac{35}{117}. \end{align*}\]
Another way to do conditional probability problems is to reduce the sample space, as in the example below.
3. Given the information in the following table find the probability that someone was sunburnt given that they were not wearing a hat.
| Sunburnt | Not sunburnt | ||
|---|---|---|---|
| Hat | 3 | 77 | 80 |
| No hat | 12 | 8 | 20 |
| 15 | 85 | 100 |
Solution:
Let \(H'\) be the event “the person is not wearing a hat”. We want \(\Pr\left(S|H'\right)\). The total sample space involves one hundred people. We can reduce this by confining out attention to those not wearing a hat. From row three of the table we see that of the 20 people not wearing a hat, 12 of them were sunburnt. So \[\begin{align*} \Pr\left(S|H'\right) & =\frac{12}{20}\\ & =\frac{3}{5}. \end{align*}\]
Exercises
1. The results of a survey of music preferences are displayed in the Venn diagram below. 4 Image from Passy’s world of mathematics. http://passyworldofmathematics.com/three-circle-venn-diagrams/
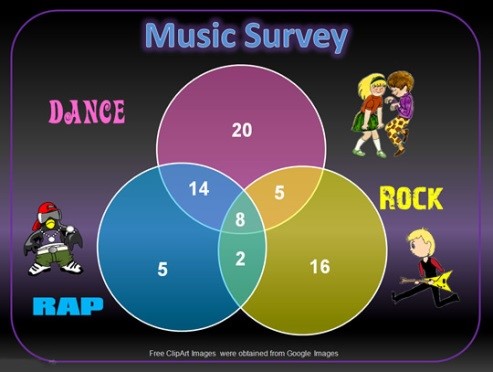
Find the probability that a student likes rock music given that they like dance music.
\(\dfrac{5+8}{14+20+8+5}=\dfrac{13}{47}\).
2. Three cards are chosen at random from a pack without replacement. What is the probability of choosing 3 aces?
\(\dfrac{4}{52}\times\dfrac{3}{51}\times\dfrac{2}{50}=\dfrac{1}{5525}\) .
3. In a maths class of 20 students 5 failed the final exam. If two students are chosen at random without replacement, what is the probability that the first passed but the second failed?
\(\dfrac{15}{20}\times\dfrac{5}{19}=\dfrac{15}{76}\)
4. If \(Pr(X)=0.5,Pr(Y)=0.5\) and \(Pr(X\cap Y)=0.2\), find the probability of
\(Pr(X|Y)\)
\(Pr(X\cup Y)\)
\(Pr(X)\times Pr(Y|X)\)
\((a)\,0.4\quad(b)\,0.8\quad(c)\,0.2\)
5. In a three child family what is the probability that all three children will be girls given that the first child is a girl.
\(0.25\)
Download this page: S7 Conditional Probability (PDF 209KB)
What's next... S8 Binomial probability
