S19 Poisson distribution

Image by Pixabay
The Poisson distribution is a discrete distribution like the binomial distribution. It was developed in the 1800s when mathematicians were asked to theorise on such matters as the annual number of wrongful criminal convictions in a particular country or to work out the number of soldiers in the Prussian cavalry who were likely to be kicked to death by a horse (honest!).
The Poisson distribution measures the probability that a certain number of random independent events occur within a period of time (or distance or area etc) when the average rate of occurrence is known.
Examples of events described by a Poisson distribution distribution are:
the number of people who enter a shop every hour
the number of flaws in a sheet of glass
the numbers of cars that pass on a stretch of road over a certain time period
the number of telephone calls a call center receives per minute
the number of errors that occur in a system.
Definition
The Poisson distribution is defined by:
\[ Pr(X=x)=\frac{e^{-\lambda}\lambda^{x}}{x!} \] where \(\lambda\) is the mean or expected number of occurrences per unit time, distance, area or volume.
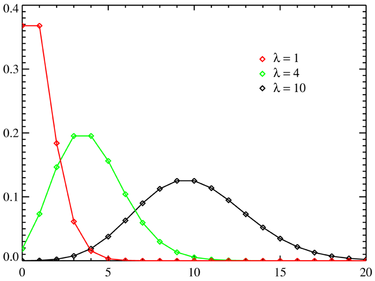
The graph below shows how the Poisson distribution varies with \(\lambda\).
Example
Let us suppose that over the past years, on average, 3 soldiers were kicked to death by horses. What is the probability that next year there will be 4 kicked to death?
In this case \(\lambda\)= 3 (the average or expected value) and \(x\) = 4 (the number of successes)
\[\begin{align*} \textrm{Using the formula }Pr(X=x) & =\frac{e^{-\lambda}\lambda^{x}}{x!}\\ Pr(X=4) & =\frac{e^{-3}3^{4}}{4!}\\ & =0.168. \end{align*}\]
The Poisson Approximation to the Binomial Distribution
You will recall that, in many instances, the normal distribution can be used to obtain fairly good approximations to binomial probabilities. The approximation works best when \(p\) is close to \(0.5\) and the approximation improves as \(n\) gets larger. As a general rule both \(np\) and \(nq\) should be greater than or equal to \(5\) in order to use the normal approximation.
But, what if \(p\) is not close to \(0.5\)? If \(p\) is small \((<0.05)\) and \(n\) is large, then we can use the Poisson distribution to approximate the binomial distribution, where the parameter, \(\lambda=np\).
Example
A sample of 50 people is chosen from a population in which 1% suffer from schizophrenia. What is the probability that 2 of these people are schizophrenic?
- Using the binomial distribution we have \(n=50\), \(p=0.01\), \(q=0.99\) so
1 Remember for a binomial distribution, where \(p\) is the probability of a success and \(q\) is the probability of a failure \(\left(q=1-p\right)\), we have \[\begin{align*} \Pr\left(X=x\right) & ={n \choose x}p^{x}q^{n-x}. \end{align*}\]
\[\begin{align*} \Pr(X=x) & ={n \choose x}p^{x}q^{n-x}\\ \Pr(X=2) & ={50 \choose 2}\times0.01^{2}\times0.99^{48}\\ & =0.0756 \end{align*}\]
- Using the Poisson approximation: \(\lambda=np=50\times0.01=0.5\) \[\begin{align*} \Pr(X=x) & =\frac{e^{-\lambda}\lambda^{x}}{x!}\\ \Pr(X=2) & =\frac{e^{-0.5}0.5^{2}}{2!}\\ & =0.0758 \end{align*}\] You can see that the Poisson distribution gives a good approximation and this approximation would be even more accurate if \(n\) was larger.
Exercises
On average one birth in every 100 produces twins. Use the Poisson distribution to find the probability that of the next 250 births there is one set of twins?
\(0.2052\)
A manufacturer of electric light globes knows from past experience that 2% of globes produced are defective. Use the Poisson distribution to approximate the probability that, out of the next 200 globes, less than 2 are defective?
\(0.0916\)
The chance of death by drowning is \(\frac{1}{30000}\) . Use the Poisson distribution to estimate the probability that, out of a random selection of 1500 people there will be at least one death by drowning.
\(0.0488\)
Insurance companies have found that the probability that a residential property is damaged by fire at some stage over a 25 year period is 0.01. If a company insures 20 houses in a particular street, use the Poisson distribution to approximate the probability that 2 of them will be damaged by fire in the next 25 years?
\(0.0164\)
