PF1.1 Newton's laws of motion
What are Newton’s first 3 laws?
An object in motion tends to stay in motion and an object at rest tends to stay at rest unless acted upon by an unbalanced force.
Force \(\left(F\right)\) equals mass \(\left(m\right)\) times acceleration \(\left(a\right)\). That is \(F=ma\).
For every action there is an equal and opposite reaction.
Net (sum of the forces or resultant) force is represented by \(\Sigma F\)
Examples
\(\sum F\)= (sum of the forces) = \(150-100=50\) Newton to the Right \(\therefore\) unbalanced force so accelerating to the right
\(\sum F\)= (sum of the forces) = \(150-100=50\) Newton to the Left \(\therefore\) unbalanced force so accelerating to the left
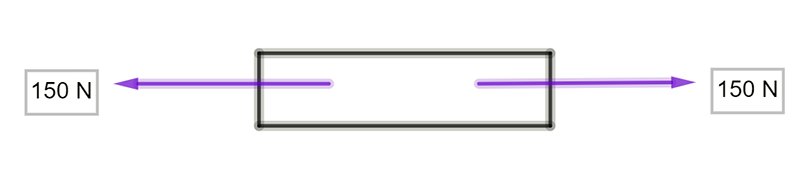
\(\sum F\)= (sum of the forces) = \(150-150=0\) Newton \(\therefore\) balanced force so is stationary or moving at a constant speed
No acceleration but could be at rest or moving at constant velocity (remember F=ma so no acceleration but it could be moving)
Note : Force is a vector quantity, so direction must be taken into consideration.
Newtons Laws of Motion
Newtons 1st law of motion
Every object continues to be at rest, or continues with constant velocity, unless it experiences an unbalanced force.
Seatbelts are fitted in cars to take into account Newtons 1st Law of Motion. If, for instance, you had to brake suddenly and you were not wearing your seatbelt, then by Newtons 1st Law, you would continue to travel at a uniform speed – the speed of the car just before braking – until you made contact with the windscreen. That is, the sum of the forces acting on you was zero at the instant you braked even though the car was being acted upon by a braking force. The windscreen would then exert a force on you as you hit it. As it did to the author of this worksheet when he was 13 years old.
Newtons 2nd law of motion
This law relates to the (sum of \(\Sigma\) ) the (forces F) written as \(\Sigma F\) s acting on an object and the acceleration produced as a consequence of this resultant force. It is given by:
Sum of the Forces = \(\Sigma F=ma\)
where \(\Sigma F\) is the sum of the forces (in Newtons), ‘m’ is the mass of the object (in\(kg\)), and ‘a’ is the acceleration (in \(ms^{-2}\)). Note: \(\Sigma F\) must have the same direction as acceleration as force is also a vector.
When doing Newtons 2nd law problems, draw all forces acting on the object in question.
Example 1
A toy car of mass \(2kg\) has a driving force \(F_{D}\) of \(20N\). The frictional force \(F_{F}\) acting on the car is \(10Newton\). Find the cars acceleration
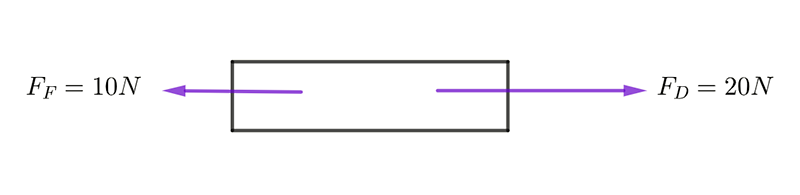
Solution:
The net force acting on the car is the driving force minus the frictional force: \[\begin{align*} \Sigma F & =F_{D}-F_{F}\\ & =20-10\\ & =10N. \end{align*}\] Using Newton’s 2nd law1 The second law is: \(\Sigma F=ma\). we get \[\begin{align*} ma & =10\\ 2a & =10\\ a & =5ms^{-2}. \end{align*}\] The magnitude of the car’s acceleration is \(5ms^{-2}\).
Newton’s 3rd law of motion
When two objects interact, the forces they exert on each other are equal in size, but opposite in direction. These pairs of forces are called action-reaction forces.
You need to appreciate that each force in the action-reaction pair acts on different objects. This is different to Newtons 2nd law where you analyze forces that are acting on the same object. Note that each force is equal in size but opposite in direction to its paired force.
Normal force \(F_{N}\)
A normal force acts at right angles to the surface with which it is in contact. For instance, if you are currently sitting on a chair reading this handout, then the chair is in contact with the floor and so there is a contact force of the chair acting on the floor given by \(F_{CF}\). By Newtons 3rd law the floor will exert an equal but opposite force on the chair of \(F_{FC}\). \(F_{FC}\) is also called the normal force \(F_{N}\). If this is not the case then you will either fall through the floor or fly up into the sky. See diagram below.
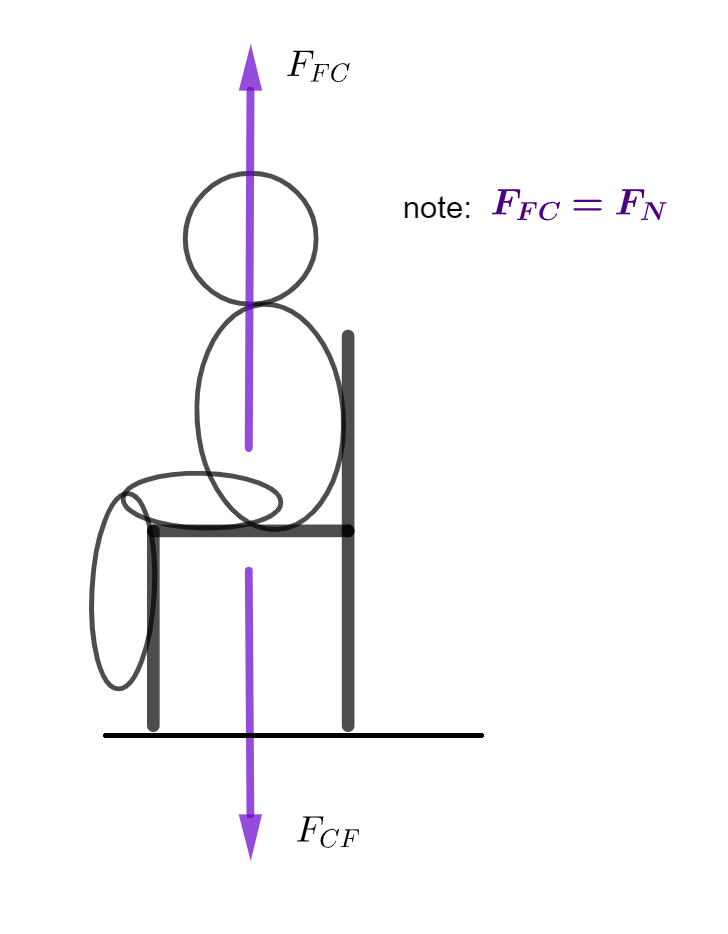
\(F_{FC}=\) \(-\) \(F_{CF}\) where the negative sign indicates that these forces are acting in opposite directions. Recall your notes on vectors. The magnitude of the forces are equal but the direction is opposite.
Applications of Newtons laws.
A starting point when analyzing Newtons 2nd law problems is to draw all forces acting on the object in question.
Objects in Lifts
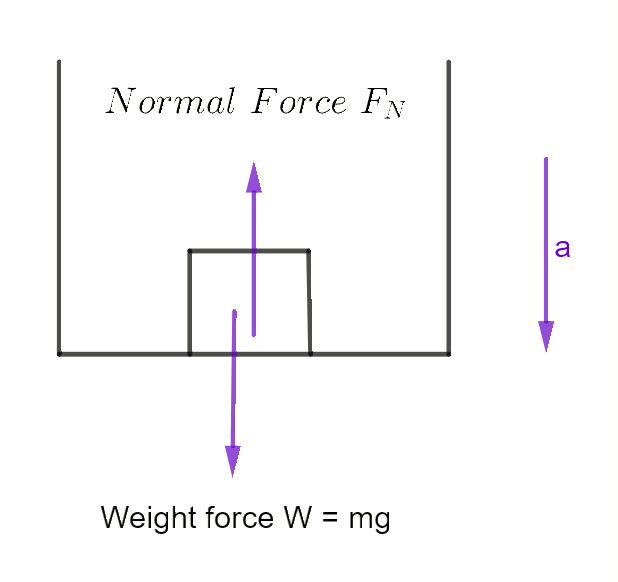
- If accelerating down (as shown): \[\begin{align*} \Sigma F & =ma\\ mg-F & =ma \end{align*}\]
Accelerating down then gravity is winning or larger. Accelerating up then Normal force is winning or larger. Acceleration has magnitude and is directional , it is a vector. where \(g\) is the acceleration of gravity (see diagram)
If accelerating up: \[\begin{align*} \Sigma F & =ma\\ F_{N}-mg & =ma \end{align*}\]
If not accelerating at all:2 It is stationary or moving at a constant velocity. \[\begin{align*} \Sigma F & =0\\ F_{N}-mg & =0\\ F_{N} & =mg \end{align*}\]
Objects Bouncing
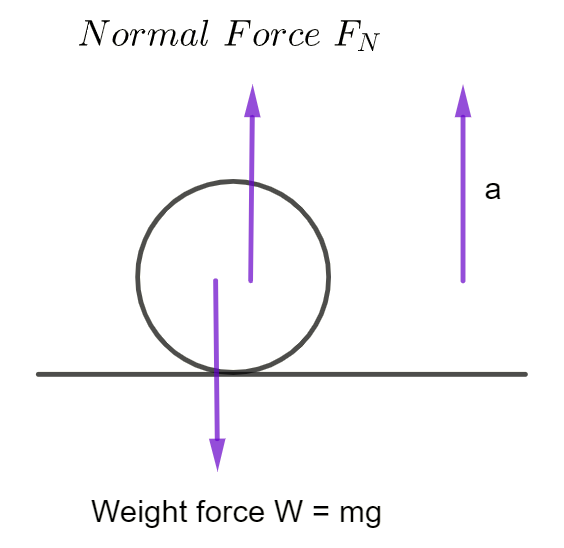
During the bounce (the instant the ball is in contact with the surface):
- \(F_{N}\) > mg, because a > 0 and is upwards. Therefore there is a resultant force acting which is upwards (as the ball will now head up).
- \(F_{N}\) can often be much larger than mg (for the ball to bounce).
- At the instant the object is stationary
(just before it changes direction and heads up)
\[\begin{align*} \Sigma F & =0\\ F_{N}-mg & =0\\ F_{N} & =mg \end{align*}\]
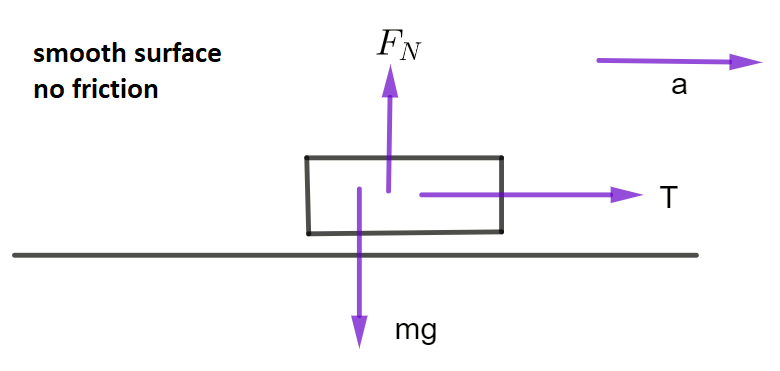
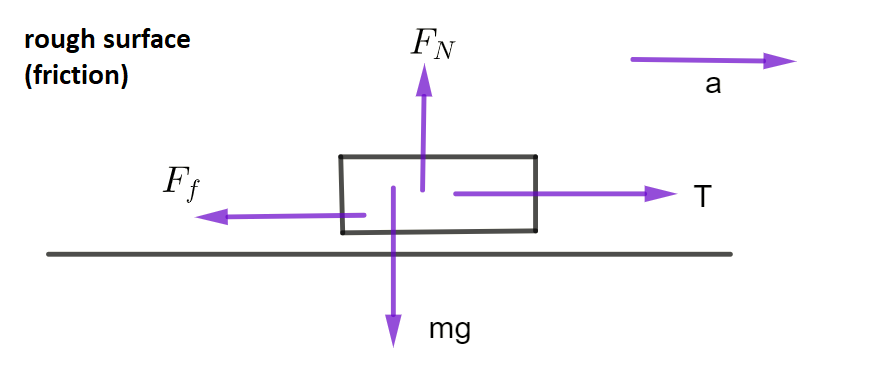
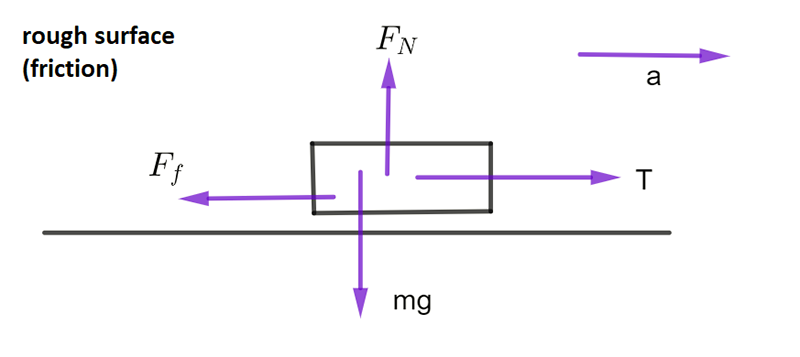
Object being pulled along a surface
\(T\) = tension in rope , \(a\) = acceleration of object , \(m\) = mass of object, \(F_{N}\) is the normal force of the table pushing on the block, \(mg\) is the force of the block pushing on the table. Remember that \(g\) is acceleration of gravity, \(F_{f}\) is the force of friction the table exerts on the object
Horizontally: \(\Sigma F\)= \(T\) \(=\) \(ma\)
Vertically: \(\Sigma F=F_{N}-mg=0\)
Therefore \(F_{N}=\) \(mg\)
Horizontally: \(\sum F\)= T - \(F_{f}\)=\(ma\)
Vertically: \(\sum F=F_{N}-mg=0\)
Therefore \(F_{N}=\) \(mg\)
Example:
A car of mass 800kg accelerates from rest to \(20\) \(ms^{-1}\) in \(\text{$8.0\sec$ }\). The resistance forces acting on the car total \(1000N\).
Find (a) the acceleration of the car, and (b) the driving force of the car.
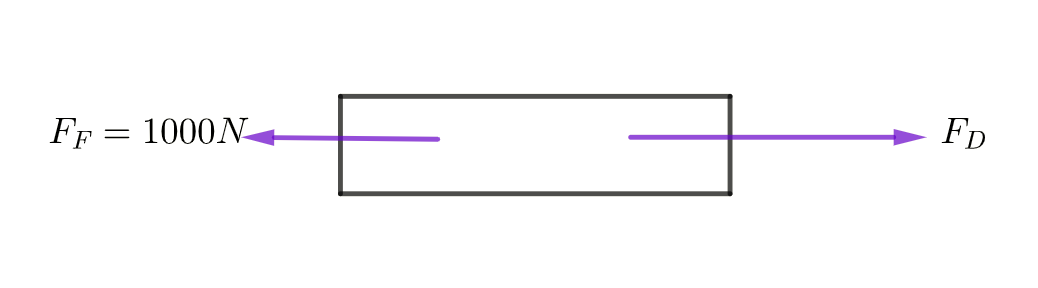
- Acceleration is given by the change in velocity divided by the time taken, or
remember “from rest” means \(u=0\), final velocity is \(v=20\) and time \(t=8\)
\[\begin{align*} a & =\frac{v-u}{t}\\ & =\frac{20-0}{8}\\ & =2.5ms^{-2} \end{align*}\]
- Net Force \(\Sigma F=F_{D}-F_{F}=ma\)
Therefore \[\begin{align*} F_{D}-F_{F} & =m\times a\\ F_{D}-1000 & =800\times2.5\\ F_{D} & =800\times2.5+1000\\ F_{D} & =2000+1000\\ F_{D} & =3000N \end{align*}\]
The driving force of the car is therefore \(3000\) Newton.
Exercise
What resultant force is needed to give a mass of 6.4 kg an acceleration of\(2.4\) \(ms^{-2}\) West?
If a resultant force of \(48\) Newton produces an acceleration of \(1.2\) \(ms^{-2}\) on an object, what is the mass of the object?
A resultant force of \(5.0\) Newton acts on an object and causes it to reach a velocity of \(4.0\) \(ms^{-1}\) in \(2.5\sec\). What is the mass of the object?
An object of mass \(6.0\) kg is at rest on a rough horizontal table. A horizontal force of \(2.4\)Newton acts on the mass to the East. The mass reaches a speed of \(1.2\) \(ms^{-1}\) in a distance of \(2.0\) meters.
Calculate the acceleration of the mass.
What is the net horizontal force acting on the object?
What is the frictional force acting on the object?
\[\begin{array}{llllll} 1)\,15\textrm{ Newtons West} & 2)\,40\,kg & 3)\,3.1\,kg & 4a)\,0.36\,ms^{-2} & 4b)\,2.2\,\textrm{Newtons East} & 4c)\,0.24\,\textrm{Newtons East}\end{array}\]
All diagrams created by RMIT staff
Download this page, PF1.1 Newton's laws of motion (PDF 255KB)