PF1.4 Momentum
The moment p of an object is the product of its mass \(m\) and velocity \(v\), or:
\[\begin{align*} p & =m\times v\\ & =kg\times m/s\\ & =kg\times ms^{-1}\\ unit\ of\ momentum & =kgms^{-1} \end{align*}\]
Note that:
- Momentum is a vector quantitiy, so it is important to remember that direction must be taken into account when doing problems on momentum.
Change in Momentum
Consider an object of mass ‘m’ changing from \(v_{i}\) to \(v_{f}\) in time \(\varDelta t\) under the action of a resultant force \(\sum F\).
From Newton’s second law of motion \(\sum F=m\times a\) and the fact that acceleration is \(a=\frac{v_{f}-v_{i}}{\varDelta t}\)
\[\begin{align*} \sum F & =m\times a\\ & =m(\frac{v_{f}-v_{i}}{\varDelta t})\\ & =\frac{mv_{f}-mv_{i}}{\varDelta t}\\ & \textrm{This transposes to the equation:} \end{align*}\]
\[\begin{align*} \sum F\times\varDelta t & =mv_{f}-mv_{i} \end{align*}\]
In other words, when a resultant force \(\sum F\) acts on an object for a time duration of \(\varDelta t\) there is a change in momentum given by ( \(mv_{f}-mv_{i}\)), where \(mv_{i}\) is the initial momentum and \(mv_{f}\) is the final momentum. This change in momentum is written as \(\varDelta p\) , or
\[\begin{align*} \varDelta p & =p_{f}-p_{i}\\ & =mv_{f}-mv_{i} \end{align*}\]
Where \(p_{i}\) is the initial momentum and \(p_{f}\) is the final momentum.
Note: one must be careful when calculating \(\varDelta p\) since change in momentum involves subracting one vector from another vector.
Impulse
As shown above, when a resultant force \(\sum F\) acts on an object for a time \(\triangle t\) the object experiences a change in momentum. The product of this resultant force and time is called the impulse I of the force.
\[\begin{align*} I & =\sum F\times\triangle t\\ & =\triangle p\\ & =mv_{f}-mv_{i} \end{align*}\]
the unit of impulse is \(Ns\).
It can be shown that since change in momentum is equal to impulse , then \(kgms\) \(^{-1}\) (kilogram meter per second) is equivalent to \(Ns\) (Newton second).
Note
As momentum and impulse are vectors , a sign convention in problems on momentum and impulse is essential.
A negative sign for the change in momentum indicates a loss of momentum; a positive sign indicates a gain in momentum.
Make sure you can do vector subtraction calculations.
Remember that \(\sum F\) is the resultant force.
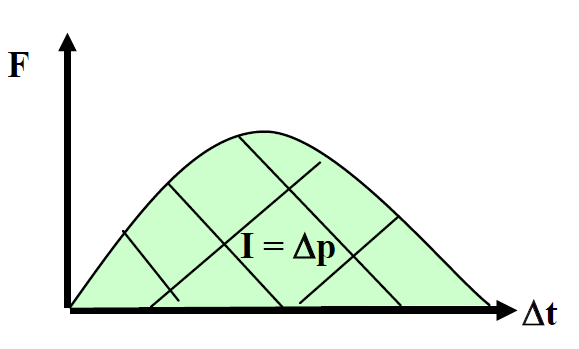
Impulse is given by the area under an \(F-\triangle t\) graph
The area under a force - time graph gives the impulse of a force. This is very useful when the force is non-uniform (see below)
\(I=\sum F\times\triangle t\) is central to much of modern car design. For instance, if a test car travelling at \(60km/h\) crashes into a wall or a large balloon (!) the change in momentum \(\triangle p\) for both will be the same. Why is it so? Hitting a wall means the force is large and time to stop is short however hitting a balloon the force is lower and the time to stop is greater, remember the final velocity is \(0\) in both cases and the mass of the car does not change.
Since \(\sum F\times\triangle t=m\times\triangle v\) then \(\sum F\times\triangle t=k\) (constant)
Hence \(F\alpha\frac{1}{\triangle t}\)
- For the wall crash: \(\triangle t\) is small. therefore F is large , ie, a larger force is acting for a smaller time.
- For the wall crash: \(\triangle t\) is large. therefore F is small , ie, a smaller force is acting for a larger time.
Conservation of Momentum
When two balls A and B collide, the action of A on B is equal and opposite to that of B on A. (Newtons 3\(^{rd}\) Law)

Hence the rate of change of momentum of A is equal and opposite to the rate of change of momentum of B. Since the time of contact is the same for both, then the change in momentum of A is equal and opposite to the change in momentum of B.
That is, the total momentum before impact equals the total momentum after impact.
\[\begin{align*} Total\ momentum\ before\ collision & =Total\ momentum\ after\ collision\\ \sum p_{i} & =\sum p_{f} \end{align*}\]
Note: This is known as the law of conservation of momentum. The total momentum is the same before , during and after impact, or
\[\begin{align*} m_{A}u_{A}+m_{B}u_{B} & =m_{A}v_{A}+m_{B}v_{B} \end{align*}\]
where \(m\) \(_{A}=\) mass of A, \(m\) \(_{B}\)= mass of B,
\(u\) \(_{A}\) = velocity of A before impact, \(u\) \(_{B}\)= velocity of B before impact,
\(v\) \(_{A}=\) velocity of A after impact, \(v\) \(_{B}=\) velocity of B after impact.
Note
Always draw a diagram when doing momentum problems.
A sign convention (+, ) is essential (momentum and impulse are vectors). Be careful with negative and positive signs!
If, for instance, the two cars collide and stay together after the collision, then the momentum of the two cars before the collision is equal to the momentum of the lockedtogether cars after the collision.
Mathematically, problems on collisions or explosions are similar, except that for an explosion, the momentum of the system before the blast is often zero.
In closed systems no external forces act. For example, a spacecraft colliding in deep space experiences no external force because there is no gravitational field. Systems close to the Earths surface are systems that are not closed because the external force acting is the Earths gravitational force. To make them closed one has to include the Earth as part of the system.
Momentum transfer involving the Earth
The following two situations describe how momentum is transferred to the Earth.
- A ball is thrown up: it rises against gravity and then slows down and stops, losing momentum due to the earth. The ball starts to fall under the influence of gravity, speeding up thereby giving the earth an equal and opposite momentum change. The falling ball hits the ground. The momentum is not lost. It is transferred to the earth.
- A bicycle on the flat is slowed down due to friction. The loss of momentum of the bike is transferred to the earth which gains an equal and opposite momentum.
Exercise
- A tennis ball of mass \(100\) gram hits the wall horizontally at \(8.0ms^{-1}\) east and rebounds at \(6.0ms^{-1}.\) The contact time with the was is \(0.07\) seconds. Calculate (a) the impulse on the ball by the wall,
- the change in momentum of the ball. State the magnitude and direction for (a) and (b)
Referring to Question1 above, calculate (a) the force exerted on the ball by the wall, and (b) the force exerted on the wall by the ball. State the magnitude and direction for (a) and (b)
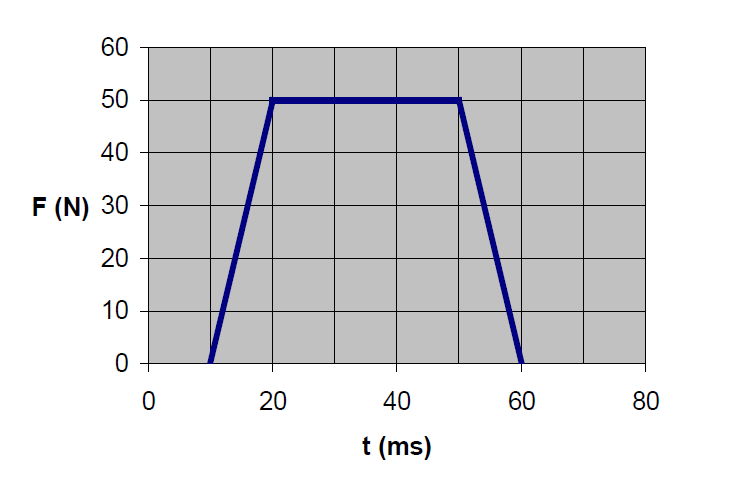
The graph shown below shows how force varies with time for a miniature crash test dummy of mass \(2kg\) moving to the right. It is involved in a collision with a large concrete block set into the ground which brings it to rest. Calculate the dummys initial speed.
A truck of mass \(2500kg\) travelling at \(20ms^{-1}\) west collides head on with a car of mass \(800kg\) travelling in the opposite direction at \(15ms^{-1}\). The two vehicles become locked together. (a) What is the total momentum of the two vehicles before the collision? Assume the trucks motion (west) is positive. (b) What is the speed and direction of the car and truck immediately after the collision?
A racing car negotiating a tight bend at \(30kmh^{-1}\) collides with a crash barrier. The air bag in his car inflates and the time taken for it to inflate is \(0.16s\). The drivers head has a mass of \(7.0kg\). Explain why the driver is less likely to suffer head injury in a collision with the air bag than if his head collided with the car dashboard, or other hard surface.
\[\begin{array}{llll} 1. a) & 1.4Ns\ West & 1. b) & 1.4 kgm/s\ West\\ 2. a) & 20N\ West & 2. b) & 20N\ East\\ 3.) & 10m/s & & \\ 4. a) & 3.8\times10^{4}kgm/s & 4. b) & 12m/s\ West\\ \end{array}\]
5.) \(F\times\varDelta t=k\) (constant), since \(m\times\triangle v\) is a constant hence , \(F\alpha\frac{1}{\triangle t}\)
In other words, the force of impact is inversely proportional to the time of impact.
For the dashboard impact: \(\triangle t\) is small, therefore F is large, resulting in serious injury.
For the air bag impact: \(\triangle t\) is large, therefore F is small, resulting in a much less serious injury.
