PMO1.2 Linear motion: Graphs
Linear motion refers to the motion of an object in a straight line. Describing these motions require some technical terms such as displacement, distance, velocity, speed and acceleration. The terms and their relationships to one another are described in this module.
Scalar and Vector Quantities
Quantities that have only a magnitude and no specified direction are called scalar quantities. Examples are time, speed and distance. Quantities that have both magnitude and direction are called vector quantities. Examples are displacement, velocity and acceleration. We discuss these below.
Displacement \(\left(x\right)\)
When an object is moved from one point to another it is said to be displaced. If we move to Dandenong we can say we have been displaced \(32\,km\) from Melbourne, but to define our position, we need to specify a direction and say we are \(32\,km\) South East of Melbourne. That is we give a magnitude (\(32\,km\)) and a direction (South East). Consequently displacement is a vector quantity.
Note that displacement is often referred to as position.
Distance \(\left(d\right)\)
Distance is the magnitude (size) of the displacement, but has no direction so it is a scalar quantity. For example you can say my distance is \(60\,km\) away, but your displacement is \(60\,km\) in a direction - such as \(60\,km\) West.
Velocity \(\left(v\right)\)
Velocity \(v\) is the rate of change of displacement \(x\). That is, for an object moving at constant velocity, \[\begin{align*} v & =\frac{x}{t} \end{align*}\] where \(t\) is the time taken. Since displacement is a vector quantity, so is velocity. The units of velocity depend on the units of displacement and time. If displacement is in metres \(\left(m\right)\) and time is in seconds \(\left(s\right)\) the unit of velocity is metres per second and is written as \(m/s\) or \(ms^{-1}.\) 1 Note that \(m/s\) is metres divided by seconds. The notation \(ms^{-1}\) uses indicial notation. Here \(s^{-1}=1/s\) and so \[\begin{align*} ms^{-1} & =m\times s^{-1}\\ & =m\times\frac{1}{s}\\ & =\frac{m}{s}. \end{align*}\]
Speed
The speed of an object is the magnitude (size) of it’s velocity. It has no direction and so is a scalar quantity.
Acceleration \(\left(a\right)\)
Acceleration is the rate of change of velocity. That is \[\begin{align*} a & =\frac{v}{t}. \end{align*}\] If \(v\) is in metres per second, the unit of acceleration is metres per second per second2 The notation \(ms^{-2}\) uses indicial notation. Here \(s^{-2}=1/s^{2}\) and so \[\begin{align*} ms^{-2} & =m\times s^{-2}\\ & =m\times\frac{1}{s^{2}}\\ & =\frac{m}{s^{2}}\\ & =m/s^{2}. \end{align*}\] and is written as \(m/s^{2}\) or \(ms^{-2}.\) Since velocity is a vector quantity, so too is acceleration.
Distance vs Time Graphs
Let’s suppose a person, starting from rest, runs a distance \(\left(d\right)\) of \(12\,m\) in a time \(\left(t\right)\) of \(2\,s.\) We could graph this as:3 Here we are assuming that the speed is constant.
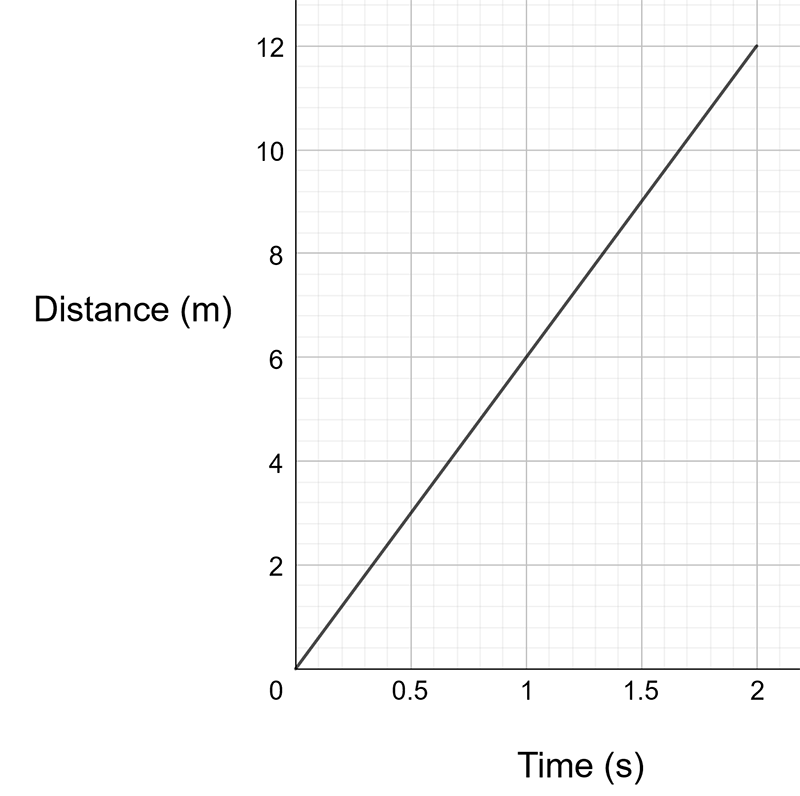
Note that the gradient of a distance (a scalar quantity) versus time graph gives the speed (also a scalar quantity). In this case, the speed is given by \[\begin{align*} \text{speed} & =\frac{d}{t}\\ & =\frac{12}{2}\\ & =6\,m/s. \end{align*}\]
Displacement vs Time Graphs
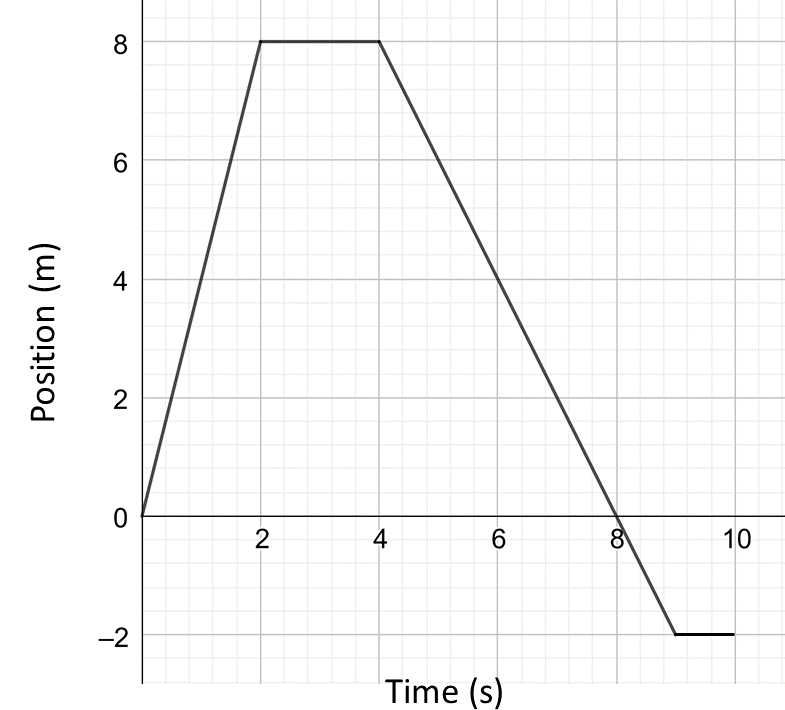
Consider the graph below:
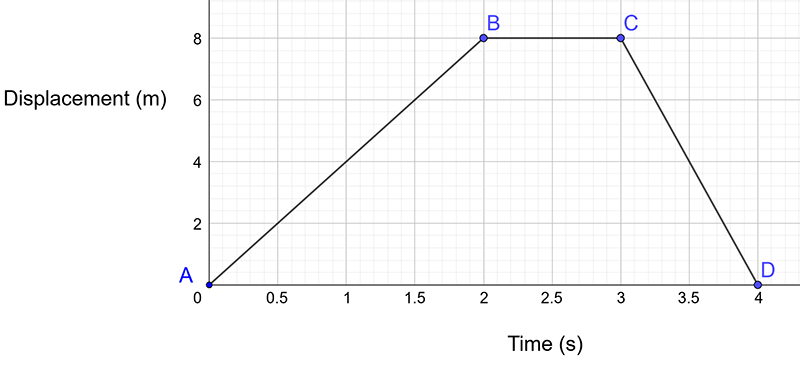
Note that this is displacement (a vector quantity) versus time. Whereas the gradient of the distance versus time graph gave speed, the gradient of the displacement (a vector) versus time graph gives velocity (a vector).
Looking at the graph, from A to B the object is moving at a constant velocity (because the graph is a straight line). Its velocity \(v\) is the gradient of the line from A to B. That is \[\begin{align*} \text{$v$ } & =\frac{displacement\;at\;\text{B$-displacement\;at\;A$ }}{time\;at\;\text{B$-time\;at\;\text{A}$ }}\\ & =\frac{8-0}{2-0}\\ & =4\,m/s. \end{align*}\]
Now consider what happens from B to C. There is no change in displacement and so \[\begin{align*} \text{$v$ } & =\frac{displacement\;at\;\text{C$-displacement\;at\;B$ }}{time\;at\;\text{C$-time\;at\;\text{B}$ }}\\ & =\frac{8-8}{3-2}\\ & =\frac{0}{1}\,m/s\\ & =0\,m/s \end{align*}\] That is, the object has a velocity of \(0\,m/s\) between B and C.
Now consider what happens from C to D. The displacement decreases from \(8\) to \(0\) over a time of \(1\,s.\) So the velocity is \[\begin{align*} \text{$v$ } & =\frac{displacement\;at\;\text{D$-displacement\;at\;C$ }}{time\;at\;\text{D$-time\;at\;\text{C}$ }}\\ & =\frac{0-8}{4-3}\\ & =-\frac{8}{1}\\ & =-8\,m/s. \end{align*}\] This means the object has reversed (due to the negative sign) its direction and is moving at a SPEED of \(8\,m/s.\)
At D, the object has returned to its starting position.
Velocity vs Time Graphs
The velocity-time graph below shows a car which accelerates uniformly from rest to \(60\,m/s\) in \(20\,s,\)then travels at a constant velocity of \(60\,m/s\) for the next \(10\,s\), then decelerates uniformly to rest in \(30\,s.\) The total journey took \(60\,s.\)
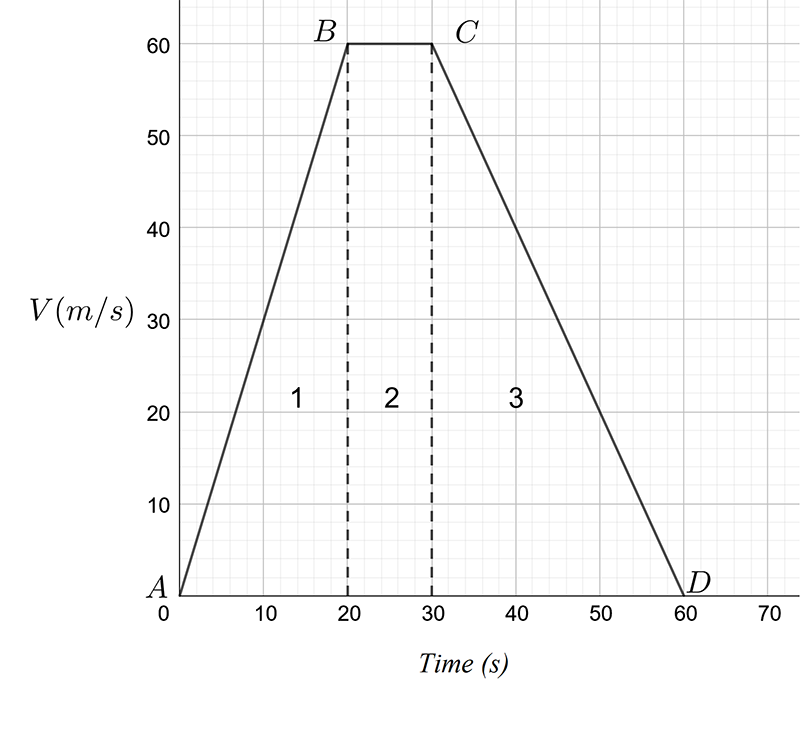
From \(A\) to \(B\), the object accelerates from \(0\,m/s\) to \(60\,m/s\). From \(B\) to \(C\) the object is moving at a constant velocity of \(60\,m/s\) and from \(C\) to \(D,\)the object is slowing down from \(60\,m/s.\) We now look at some features of the graph in detail. In particular we look at the area under the graph and it’s gradient.
Area Under Velocity Time Graph
Consider the units of the area. The area is the product of the velocity and time and so the units are \(m/s\,\times s=m.\) That is, the area under the graph gives displacement.
The area under a velocity-time graph gives displacement.
The area under a speed-time graph gives distance.
Consider the velocity time graph above. The area has been divided into three regions, \(1,2\) and \(3.\) Let area of each region be \(A_{1},A_{2}\) and \(A_{3},\)respectively. We have:4 Remember that the area of a triangle \(A_{t}\) is half \(\times\)base \(\times\) height and the area of a rectangle \(A_{r}\) is base \(\times\) height. That is, \[\begin{align*} A_{t} & =\frac{1}{2}\times b\times h\\ & =\frac{1}{2}bh\\ A_{r} & =b\times h\\ & =bh. \end{align*}\]
\[\begin{align*} A_{1} & =\frac{1}{2}\times b\times h\\ & =\frac{1}{2}\times20\times60\\ & =600\,m\\ A_{2} & =b\times h\\ & =10\times60\\ & =600\,m\\ A_{3} & =\frac{1}{2}\times b\times h\\ & =\frac{1}{2}\times30\times60\\ & =900\,m. \end{align*}\] The total displacement is therefore \(A_{1}+A_{2}+A_{3}=600+600+900=2100\,m.\)
Gradient of a Velocity-Time Graph
The gradient (or slope)5 The gradient \(m,\) of a linear (straight line) graph is the rise divided by the run. That is, \[\begin{align*} m & =\frac{\text{rise}}{\text{run}}. \end{align*}\] of a Velocity-Time graph gives the acceleration of the object.
Consider the velocity-time graph above. From \(A\) to \(B\) the gradient of the graph is \(m_{AB}\) where \[\begin{align*} m_{AB} & =\frac{\text{rise}}{\text{run}}\\ & =\frac{\text{change in velocity}}{\text{change in time}}\\ & =\frac{60-0}{20-0}\\ & =\frac{60}{20}\\ & =3\,ms^{-2}. \end{align*}\] That is, the car is increasing its speed by \(3\,m/s\) each second.
From \(B\) to \(C\) the gradient \[\begin{align*} m_{BC} & =\frac{\text{rise}}{\text{run}}\\ & =\frac{\text{change in velocity}}{\text{change in time}}\\ & =\frac{60-60}{30-20}=\\ & =\frac{0}{10}\\ & =0\,ms^{-2}. \end{align*}\] That is the car is not accelerating but is moving at a constant velocity of \(60\,m/s.\)
From \(C\) to \(D\) the gradient \[\begin{align*} m_{CD} & =\frac{\text{rise}}{\text{run}}\\ & =\frac{\text{change in velocity}}{\text{change in time}}\\ & =\frac{0-60}{60-30}=\\ & =-\frac{60}{30}\\ & =-2\,ms^{-2}. \end{align*}\] Note the negative value of acceleration indicates the car is slowing down. We say the car is decelerating.
Further examples
1. A car accelerates from a stationary position. The rate of acceleration is constant6 If acceleration is constant we also use the expression “the acceleration is uniform”. . Sketch graphs of the acceleration against time, the velocity against time and the displacement against time.
Solution:
The acceleration-time graph is shown below.
It is simply a horizontal line as the acceleration is constant.
The velocity-time graph is shown below.
It is a linear graph. The gradient (slope) of the graph is the acceleration.
The displacement-time graph is shown below.
This is a curve. The gradient (slope) at any point on the curve is the velocity at that time. You can find the approximate value of the gradient by drawing a tangent at the point of interest and then calculating the gradient of the tangent.7 If you know the functional form of the displacement, then you can differentiate it to find the gradient at any time. For example, if \[\begin{align*} x\left(t\right) & =3t^{2}-2t+1 \end{align*}\] then the gradient is \[\begin{align*} \frac{dx}{dt} & =6t-2. \end{align*}\]
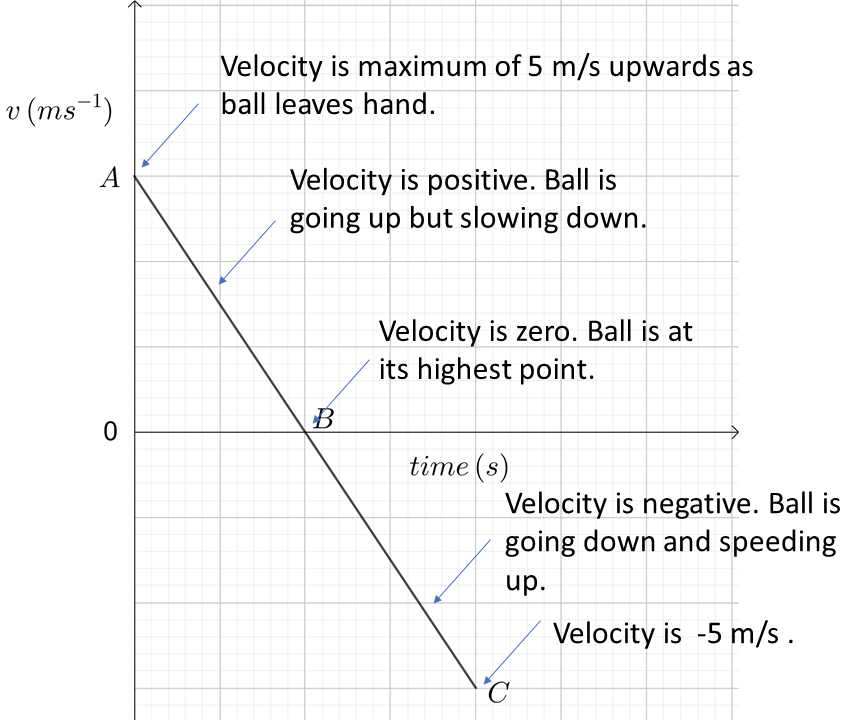
2. A ball is thrown vertically upwards with a speed of \(5\,m/s\). Sketch and describe the graph of velocity of the ball against time from the moment it is thrown to the moment it touches the ground. Ignore air resistance.
Solution:
First define the coordinate system you want to work in. We take upwards velocity as positive and downwards velocity as negative. Once the ball is thrown up, the only force acting on it is gravity which is constant. So from the previous example, the graph of velocity against time is linear. That is, a straight line. As gravity acts downwards, the velocity against time graph must have a negative gradient (because the ball is decelerating). So a velocity-time graph looks like the one below.
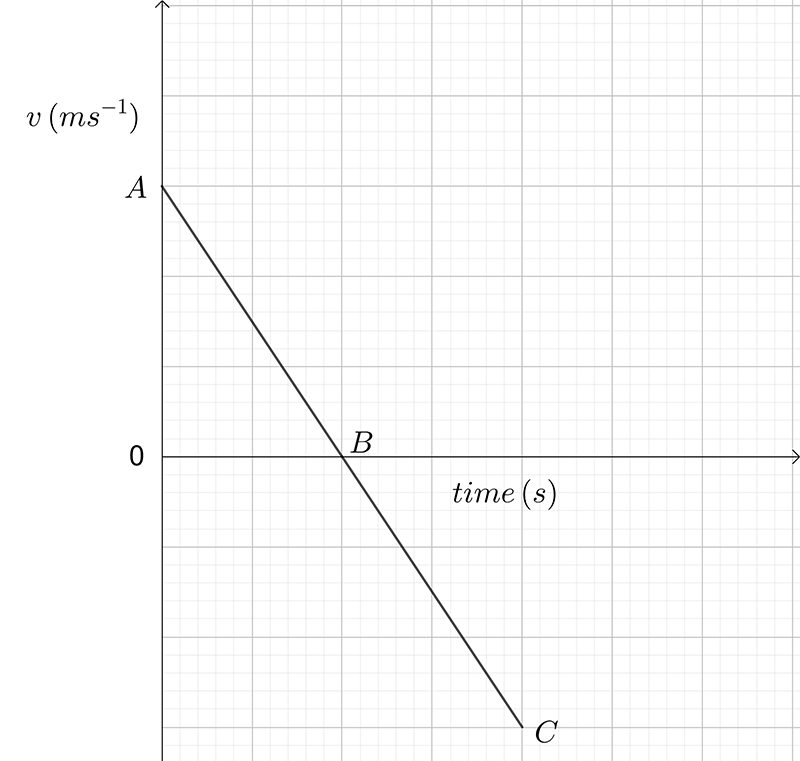
Now we need to describe it. Think about what has happened. Initially the ball is thrown into the air vertically upwards (positive direction) with a speed of \(5\,m/s\). Point \(A\) describes the initial velocity (upward) that the ball has. It is \(5\,m/s\) upward.
Then the ball starts to slow down (due to gravity acting on it). This is the part of the graph from \(A\) to \(B\). At point \(B,\) the ball has zero velocity. It is not moving, and so this is the point of maximum altitude for the ball.
After \(B,\) the ball has a negative velocity. That means it is now heading downwards towards the point from which it was thrown. Point \(C\) represents the starting position. At this point the ball has the same speed8 Speed is the magnitude of the velocity vector. At point \(A\) the velocity was \(5\,m/s\) upward. At point \(C\) the velocity is \(-5\,m/s\) or \(5\,m/s\) downward. Remember, a vector quantity has to have a magnitude and a direction. as it had at point \(A.\) This is shown in the diagram below.
Summary
The relationships between various graphs and their gradient and the area below them are summarized in the table below:
| Graph Type | Displacement vs time | Velocity vs time | Acceleration vs time | |
|---|---|---|---|---|
| Gradient | Velocity | Acceleration | No Meaning | |
| Area under graph | No Meaning | Displacement | Change in velocity |
Exercise
- The graph below shows the position of a dancer moving in a straight line across a stage.
The dancer’s movements are designated by sections \(A\) to \(D.\)
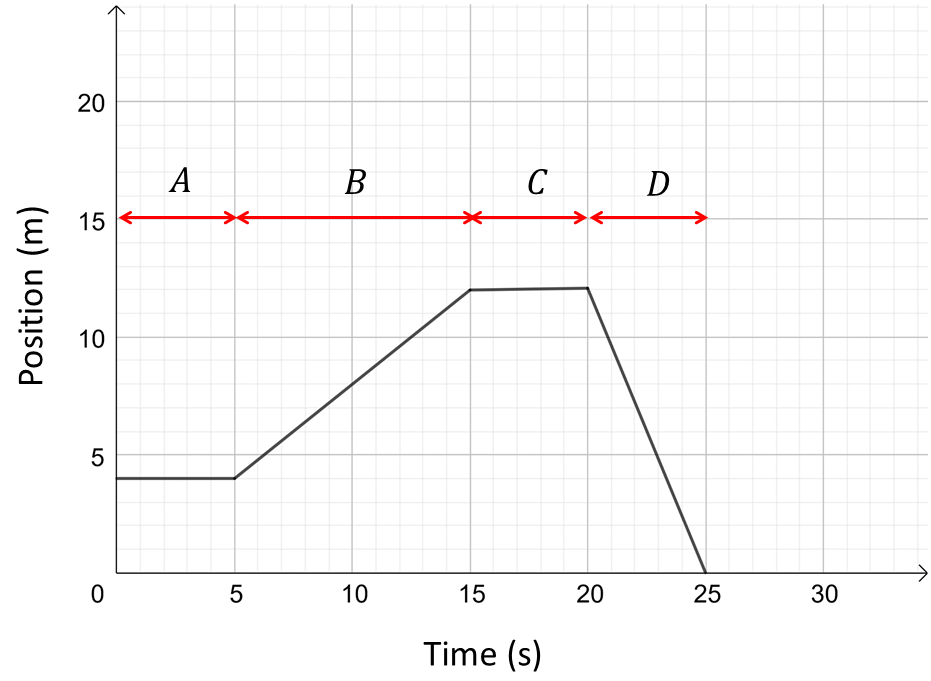
- What was the starting position of the dancer?
- In which of the sections (\(A\) - \(D)\) is the dancer at rest?
- In which of the sections is the dancer moving in a positive direction?
- In which of the sections is the dancer moving with a negative velocity?
- The graph below represents the straight line motion of a radio-controlled toy car.
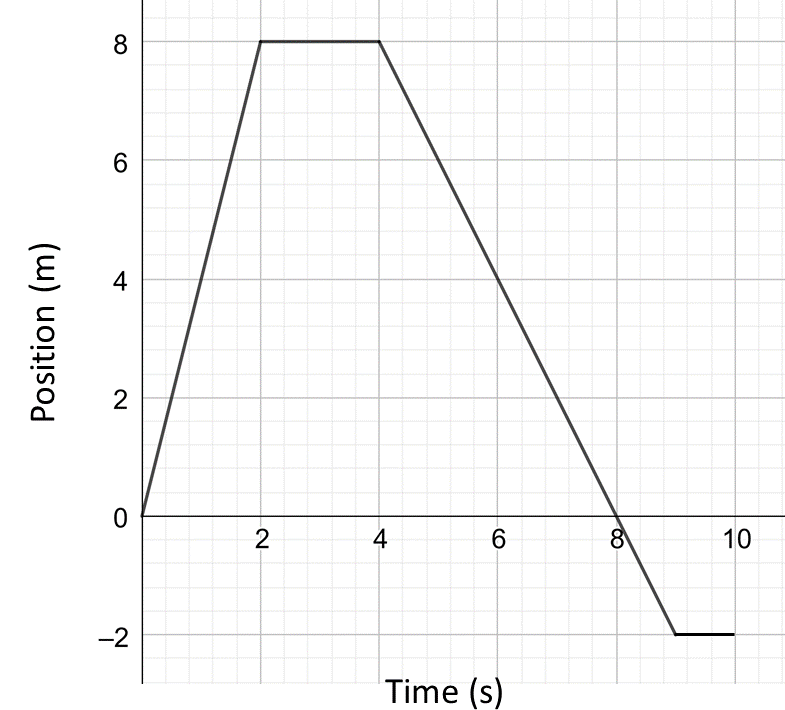
- Describe, in words, the motion of the car.
- What was the position of the car after i) \(2\,s\) ii) \(4\,s\) iii) \(6\,s\) iv) \(10\,s\) ?
- At what time did the car return to its starting point?
- What was the velocity of the car
\(\qquad\)i) during the first \(2\,s\) ?
\(\qquad\)ii) after \(3\,s\) ?
\(\qquad\)iii) from \(4\,s\) to \(6\,s\) ?
\(\qquad\)iv) at \(8\,s\) ?
\(\qquad v)\) from \(8\,s\) to \(9\,s\) ?
- During its \(10\,s\) motion, what was the car’s
\(\qquad\)i) distance traveled?
\(\qquad\)ii) displacement?
- The following position-time graph is for a cyclist traveling along a straight road.
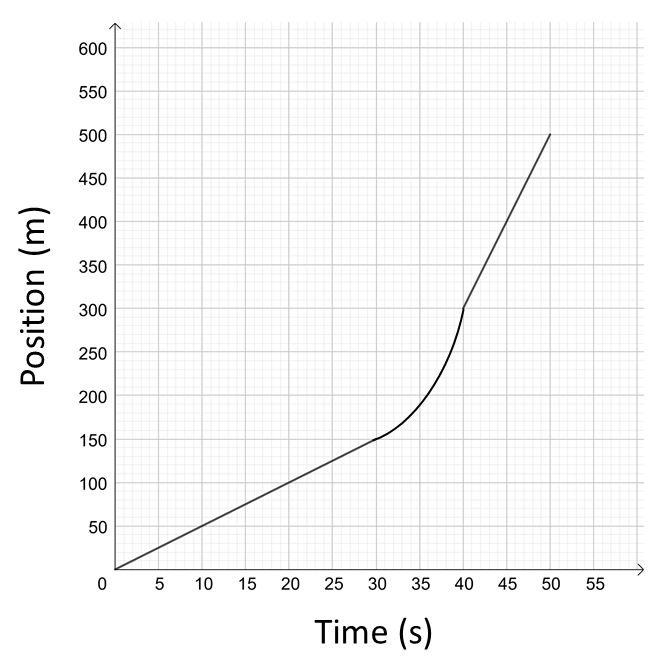
- Describe the motion of the cyclist in words.
- What was the velocity of the cyclist during the first \(30\,s\)?
- What was the cyclist’s velocity during the final \(10\,s\)?
- Calculate the cyclist’s instantaneous velocity at \(35\,s.\)
- What was the average velocity of the cyclist between \(30\,s\) and \(40\,s\)?
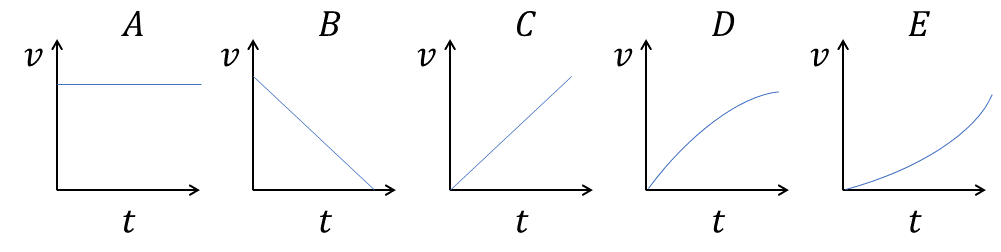
- Which of the velocity-time graphs \(A\) to \(E\) best represents the motion of:
- a car coming to a stop at a traffic light?
- a swimmer moving at a constant speed?
- a cyclist accelerating from rest with constant acceleration?
- a car accelerating from rest and changing through its gears.
- The following graph shows the motion of a dog running along a footpath in a northerly direction.
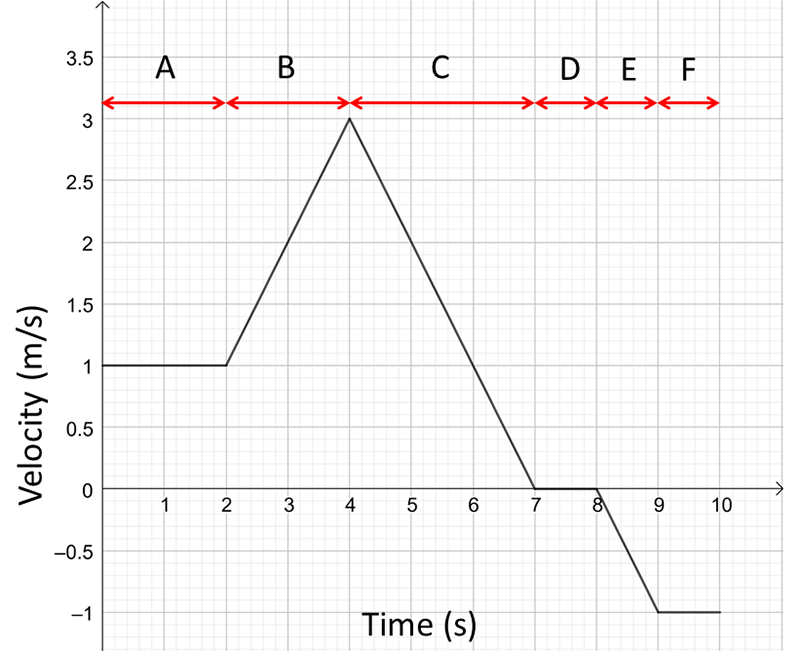
- Describe the motion of the dog during these sections of the graph:
\(\qquad\)i) A\(\quad\;\)ii) B\(\quad\;\)iii) C\(\quad\;\)iv) D\(\quad\;\)v) E\(\quad\;\)vi) F.
- Calculate the displacement of the dog after:
\(\qquad\)i) \(2\,s\quad\;\)ii) \(7\,s\quad\;\)iii) \(10\,s.\)
- Plot a position-time graph of the dog’s motion.
- The straight line motion of a train is shown below:
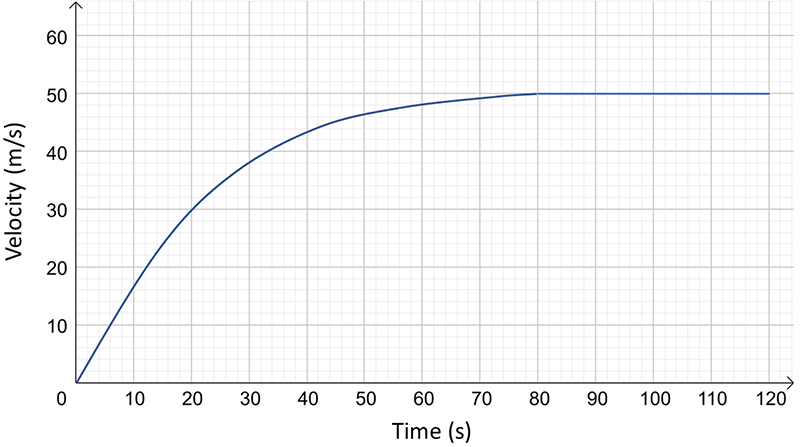
- How long does the train take to reach its cruising speed?
- What is the acceleration of the train \(10\,s\) after starting.
- What is the acceleration of the train \(40\,s\) after starting?
- What is the displacement of the train after \(120\,s\) ?
Hint for b.9 You can only approximate this. Take a tangent to the graph at \(10\,s\) and calculate its gradient.
- The velocity-time graphs for a bus and a bicycle traveling along the same
straight stretch of road are shown below.
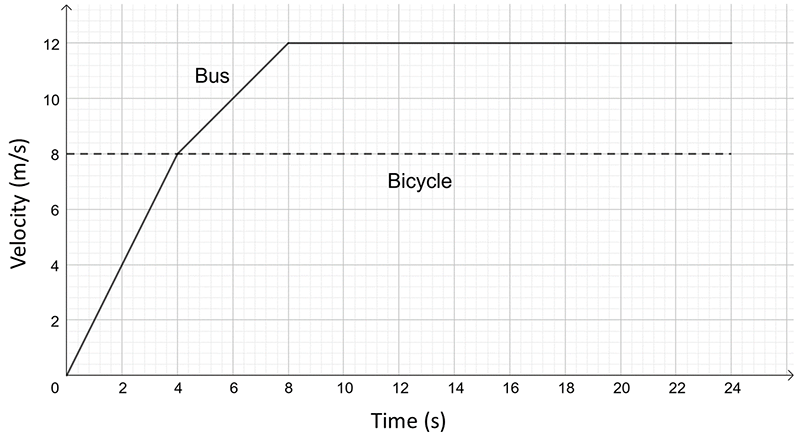
The bus is initially at rest and starts moving as the bicycle passes it.
a) Calculate the initial acceleration of the bus.
b) When does the bus first start gaining ground on the bicycle?
c) At what time does the bus overtake the bicycle?
d) How far has the bicycle traveled before the bus catches it?
e) What is the average velocity of the bus during the first \(8\,s\)?
f) Draw an acceleration-time graph for the bus.
g) Use your acceleration-time graph to determine the change in velocity of the bus over the first \(8\,s\) .
- \(+4\,m\qquad\text{b}.\,A,\,C\qquad\text{c}.\,B\qquad\text{d}.\,D\)
- a The car initially moves in a positive direction and travels \(8\,m\) in \(2\,s.\) It then stops for \(2\,s.\) The car then reverses direction for \(5\,s\), passing back through its starting point after \(8\,s.\) It then travels a further \(2\,m\) in a negative direction before stopping after \(9\,s.\)
- \(+8\,m\qquad\text{ii. $+8\,m\qquad$ iii. $+4\,m\qquad$ iv. $-2\,m$ .}\)
- \(+8\,m\qquad\text{ii. $+8\,m\qquad$ iii. $+4\,m\qquad$ iv. $-2\,m$ .}\)
- \(8\,s\)
- \(+4\,m/s\qquad\text{ii. $0\qquad$ iii. $-2\,m/s\qquad$ iv. $-2\,m/s$ .}\)
- \(+4\,m/s\qquad\text{ii. $0\qquad$ iii. $-2\,m/s\qquad$ iv. $-2\,m/s$ .}\)
- \(18\,m\qquad\text{ii. $-2\,m$ .}\)
- a The cyclist travels with a constant velocity in a positive direction for the first \(30\,s\) and travels \(150\,m\) in this time. Then the cyclist speeds up for the next \(10\,s\) traveling a further \(150\,m.\) Finally the cyclist maintains the increased speed for the final \(10\,s\) and covers another \(200\,m\) in this time.
- \(+5\,m/s\qquad\text{c. $+20\,m/s\qquad$ d. $\text{approximately $13\,m/s$ }\qquad$ e. $+15\,m/s$ .}\)
a \(B\qquad\text{b $A\qquad$ c $C\qquad$ d $D$ .}\)
a i. Running north at \(1\,m/s.\)
\(\;\,\)ii. Increasing speed from \(1\,m/s\) to \(3\,m/s\) while running north.
\(\;\,\)iii. Running north but slowing to a stop.
\(\;\,\)iv. Stationary.
\(\;\,\)v. Accelerating from rest to \(1\,m/s\) while traveling south.
\(\;\,\)vi. Running south at \(1\,m/s.\)
b Position-time graph of dog’s motion
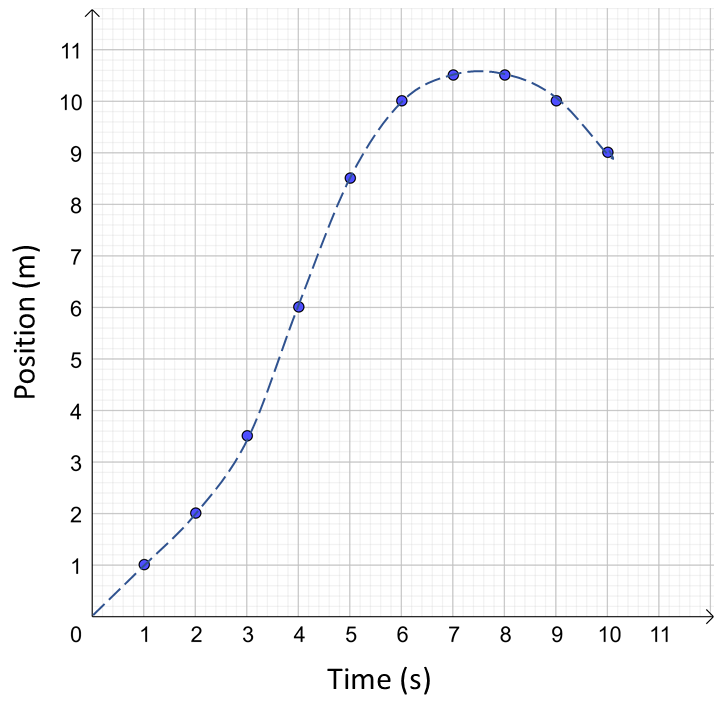
a \(80\,s\qquad\text{b $A\qquad$ c $C\qquad$ d $D$ .}\)
- \(+2\,m/s\quad\text{b}.\;4\,s\quad\text{c}.\,10\,s\quad\text{d. $80\,m$ $\quad\text{e. $+7\:m/s$ }$ }\)
- \(+2\,m/s\quad\text{b}.\;4\,s\quad\text{c}.\,10\,s\quad\text{d. $80\,m$ $\quad\text{e. $+7\:m/s$ }$ }\)
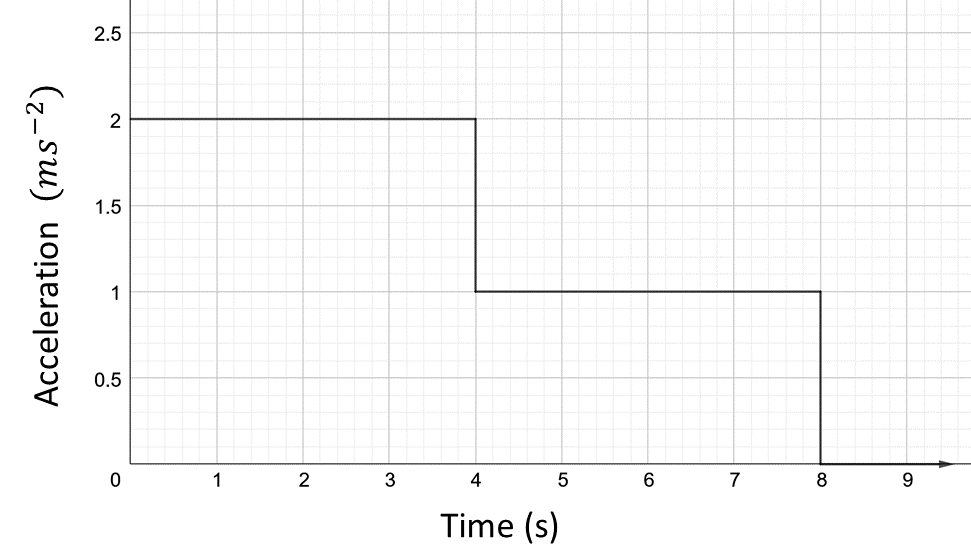
- Change in velocity is area under the Acceleration-Time graph \(=8+4=12\,m/s.\)
Download this page, PMO1.2 Linear motion: Graphs (PDF 1480KB)
