ES3 Quadratic equations
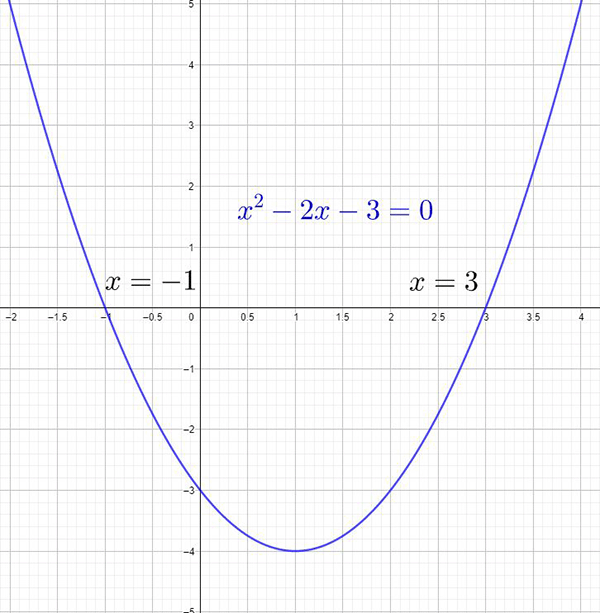
The solution to a quadratic equation gives the \(x\)- intercepts of its graph.
The general form of a quadratic equation is A X squared plus B X plus C equals zero where A is not equal to one.
Hi, I’m Martin Lindsay from the Study and Learning Centre at RMIT University. This is a short movie on solving quadratic equations.
The general form of a quadratic equation is A X squared plus B X plus C equals zero where A is not equal to one. For instance, five X squared minus three X plus nine equals zero. In this case A equals five, B equals minus three and C equals nine and if you have the equation X squared equals five X minus four you then have to rearrange it into the form A X squared plus B X plus C equals zero, in other words this becomes X squared minus five X plus four equals zero where A equals one, B equals minus five and C equals four.
Let’s start with Y squared equals five Y. As you can see this is not of the form A X squared plus B X plus C equals zero, so rearrange it to make it look like that, Y squared minus five Y equals zero. Notice that this will factorise into Y brackets Y minus five. Then we have the form M times N equals zero, Y times Y minus five equals zero, so we can use the null factor law where Y equals zero or Y minus five equals zero, from which Y equals zero or Y equals five. Notice when you get your answers it’s a good idea to check that when substituting Y equals zero and Y equals five back into the original Y squared equals five Y that you get the left hand side equal to the right hand side. Do this for yourself.
Let’s look at this example, X squared minus five X plus four equals zero. Note how it’s different to example one, there’s a trinomial here, X squared term and X term and a number term, a constant. That will factorise into X minus four X minus one, again we have our null factor law X minus four times X minus one, so using that law we get X minus four equals zero or X minus one equals zero from which X equals four or X equals one. It’s always a good idea to check to see that the answers are correct by substituting back into the original equation. You can do this for yourself.
Let’s look at another trinomial, P square plus 10 P plus 25 equals zero. This will factorise into P plus five P plus five. Notice it’s a perfect square and thus, using the null factor law, we have just one P plus five equals zero from which P equals minus five. Again, do the check to make sure the left hand side of the original equation equals the right hand side, which is zero.
Here’s another example, four M squared minus 49 equals zero. Notice that this is the difference of a perfect square, in other words it becomes two M plus seven two M minus seven equals zero. Again using the null factor law two M plus seven equals zero two M minus seven equals zero from which M equals minus seven over two or M equals plus seven over two.
And finally here’s a more complicated quadratic equation to solve. Here we’re given X equals minus six over one minus two X so we have to do some rearranging first to turn it into A X square plus B X plus C equals zero, and that’s what I’ve done in this second line, so we have two X squared minus X minus six equals zero which needs to be factorised and it does, into two X plus three X minus two equals zero, using the null factor law we arrive at X equals minus three over two or X equals two, so those are our solutions.
Now do some problems for yourselves. The answers to these six questions are on the next slide. Thanks for watching this short movie.
This tip sheet looks at solutions to quadratic equations using the “null factor law”.
General Form
A equation can be rearranged to the form: \(ax^{2}+bx+c=0\) where \(a\neq0\).
Examples
(using \(ax^{2}+bx+c=0\) determine \(a\) , \(b\) and \(c\))
\(5x^{2}-3x+9=0\) \(\quad\quad a=5,\,\) \(\ b=-3,\,\) \(\ c=9\)
\(x^{2}=5x-4\ \ \ \Rightarrow\) \(\ \ \ x^{2}-5x+4=0\quad\quad\) \(a=1,\,\) \(\ b=-5,\,\) \(\ c=4\)
\(x=\frac{3}{2x}\ \ \ \) \(\Rightarrow\ \ \ \) \(2x^{2}=3\) \(\ \ \ \Rightarrow\ \ \ \) \(2x^{2}-3=0\qquad\) \(a=1,\,\) \(\ b=0,\,\) \(\ c=-3\)
Factorisation
If the equation can be factorised then the ‘null factor law’ can be used to find the solutions:
Null factor law uses the simple idea:
If \(m\times n=0\), then \(m=0\) and / or \(n=0\)
If the product of two or more factors is zero then any one of the individual factors may be zero and provide a solution for the equation.
Example 1 (find all possible values of y)
\[\begin{alignat*}{1} y^{2} & =5y\\ y^{2}-5y & =0\,(\mathrm{\mathrm{rearrange\,}to\,form})\\ y(y-5) & =0\,(\mathrm{rearrange})\\ \mathrm{for\ this\ to\ be\ true}\\ y=0\,\ \mathrm{or}\,\, & (y-5)\ \,\mathrm{must\ equal\ zero,\ \ \ (null\,factor\,law})\\ \therefore\mathbf{\,y=0\,\,\mathrm{or}\,\,} & \mathbf{y=5}\\ \\ \mathrm{check\ by\ substututing\ back\ to\ } & y^{2}=5y\\ \mathrm{If}\,\, & y=0,\ \ 0^{2}=5\times0\mathrm{\,(checked)}\\ \mathrm{If}\,\, & y=5,\ \ 5^{2}=5\times5\,\mathrm{(checked)}\\ y^{2} & =5y\\ \mathrm{Left\,Hand\ Side}\ & \mathrm{=Right\,Hand\ Side}\\ \end{alignat*}\]
Example 2 (find all possible values of x)
\[\begin{alignat*}{1} x^{2}-5x+4 & =0\\ (x-4)(x-1) & =0\,\mathrm{\ (factorise)}\\ (x-4)=0\,\ \,\mathrm{or}\,\ \, & (x-1)=0\,\ \ \mathrm{(null\,factor\,law})\\ \mathbf{\therefore\ x=4\,\,\mathrm{or}}\,\, & \mathbf{x=1}\\ \\ \mathrm{check\ by\ substututing\ back\ to\ } & x^{2}-5x+4=0\\ \mathrm{If}\,\, & x=4,\ \ 4^{2}-5\times4+4=0\mathrm{\,(checked)}\\ \mathrm{If}\,\, & x=1,\ \ 1^{2}-5\times1+4=0\mathrm{\,(checked)}\\ \end{alignat*}\]
Example 3 (find all possible values of p)
\[\begin{alignat*}{1} p^{2}+10p+25 & =0\\ (p+5)(p+5) & =0\,\mathrm{\ \ (factorise)}\\ (p+5) & =0\ \ \,\mathrm{(null\,factor\,law})\\ \therefore\mathbf{\ p} & \mathbf{=-5}\\ \\ \mathrm{check\ by\ substututing\ back\ to\ } & p^{2}+10p+25=0\\ \mathrm{If}\ p=-5\,\,\mathrm{check} & (-5)^{2}+10\times(-5)+25=0\\ \end{alignat*}\]
Example 4 (find all possible values of m)
\[\begin{alignat*}{1} 4m^{2}-49 & =0\\ (2m+7)(2m-7) & =0\,\mathrm{(factorise\,by\,difference\,of\,squares)}\\ (2m+7)=0\,\mathrm{or}\,\, & (2m-7)=0\,\mathrm{(null\,factor\,law)}\\ \mathbf{\therefore\ m=\frac{-7}{2}\ \ \,\mathrm{or}}\,\ \, & \mathbf{m\mathbf{=\frac{7}{2}}}\\ \\ \mathrm{check\ by\ substututing\ back\ to\ } & 4m^{2}-49=0\\ \end{alignat*}\]
Example 5 (find all possible values of x)
\[\begin{alignat*}{1} x=\frac{-6}{1-2x}\,\,\mathrm{provided}\,\, & x\neq1/2\\ x-2x^{2} & =-6\mathrm{\ \ \ (multiplying\ both\ sides\ by}\ 1-2x)\\ 2x^{2}-x-6 & =0\,\ \ \mathrm{(rearrange\,to\,form\,\,}ax^{2}+bx+c=0)\\ (2x+3)(x-2) & =0\,\ \ \mathrm{(factorise)}\\ \mathbf{\therefore\ x=\frac{-3}{2}\,\mathrm{\ \ or\ }\,\,x} & \mathbf{=2\,}\ \ \,\mathrm{(solving\,using\,null\,factor\,law)}\\ \end{alignat*}\]
Exercises
Solve the following quadratic equations:
\(\ \ x^{2}-6x+8=0\)
\(\ \ x^{2}+2x-3=0\)
\(\ \ 2x^{2}-3x-2=0\)
\(\ \ 6-z-z^{2}=0\)
\(\ \ 2x^{2}+7x=15\)
\(\ \ 11p=3(2p^{2}+1)\)
\[\begin{array}{ccc} 1. & \ \ x=4, & \ \ x=2\\ 2. & \ \ x=-3, & \ \ x=1\\ 3. & \ \ x=-1/2, & \ \ x=2\\ 4. & \ \ z=-3, & \ \ z=2\\ 5. & \ \ x=3/2, & x=-5\\ 6. & \ \ p=1/3, & \ \ p=3/2 \end{array}\]
Download this as a PDF file: ES3 Quadratic Equations (225KB)
What's next... ES4 Quadratic formula
