ES6 (ILS2.2) Exponential equations
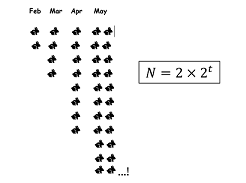
Indicial (or exponential) equations have the form ax = b If we can write b as a number with a base a and an index, then we can equate the indices to find x. If two equal numbers are written to the same base then the indices must be equal.
Exponential equations have a term in which the variable appears as a power (index or exponent).
For example: \[\begin{align*} 2^{1-x} & =4^{3x}\\ \mathrm{or,\quad}\ 5^{x} & =17. \end{align*}\]
To solve exponential equations we may make use of the properties:
\[ m^{x}=m^{y}\Rightarrow x=y\quad\left(1\right) \]
\[ m^{x}=y\Rightarrow\log_{a}m^{x}=\log_{a}y\quad\left(2\right) \]
Examples
Solve \(3^{x}=27\)
\[\begin{align*} 3^{x} & =27\\ 3^{x} & =3^{3}\\ x & =3,\ \textrm{using property $\left(1\right)$ .}\textrm{ } \end{align*}\]Solve \(2^{1-x}=\frac{1}{8}\) \[\begin{align*} 2^{1-x} & =\frac{1}{8}\\ 2^{1-x} & =2^{-3}\textrm{ }\\ 1-x & =-3\ \textrm{using property $\left(1\right)$ }\\ x & =4. \end{align*}\]
Solve \(5^{\frac{1}{x}}=25\)
\[\begin{align*} 5^{\frac{1}{x}} & =25\\ 5^{\frac{1}{x}} & =5^{2}\\ \frac{1}{x} & =2\ \textrm{using property $\left(1\right)$ }\\ x & =\frac{1}{2}. \end{align*}\]
Non Integer Solutions
Not all equations have integer solutions.1 An integer is a whole number. We denote the set of integers by the symbol \(\mathbb{Z}.\) \[\begin{align*} \mathbb{Z} & =\left\{ \ldots,-2,-1,0,1,2,\ldots\right\} \end{align*}\]
For example: \(3^{x}=10\) has a solution between 2 and 3 since \(3^{2}=9\) and \(3^{3}=27\).
Logarithms with base \(10\) or base \(e\) can be used to solve such equations with the calculator.
On the calculator the LOG button will calculate \(\log_{10}x\) and the LN button will calculate \(\log_{e}x\). Logarithms with base e are known as natural logarithms and sometimes the abbreviation \(\ln x\) is used for \(\log_{e}x.\)
Examples
- Solve \(3^{x}=10\) to 3 decimal places.
Solution:
\[\begin{align*} 3^{x} & =10\\ \log_{10}3^{x} & =\log_{10}10\textrm{ }\\ x\log_{10}3 & =1\textrm{ }\\ x & =\frac{1}{\log_{10}3}\\ x & =2.095. \end{align*}\]
Solve \(2\times5^{x+1}=15\) to two decimal places.
Solution: \[\begin{align*} 2\times5^{x+1} & =15\\ 5^{x+1} & =7.5\\ \log_{10}5^{x+1} & =\log_{10}7.5\\ (x+1)\log_{10}5 & =\log_{10}7.5\\ x+1 & =\frac{\log_{10}7.5}{\log_{10}5}\\ x+1 & =1.25\\ x & =0.25. \end{align*}\]Solve \(2^{2x+1}=5^{2-x}\) to three decimal places.
Solution:
\[\begin{align*} 2^{2x+1} & =5^{2-x}\\ \log_{10}2^{2x+1} & =\log_{10}5^{2-x}\\ (2x+1)\log_{10}2 & =(2-x)\log_{10}5\\ (2x+1)0.301 & =(2-x)0.699\\ 0.602x+0.301 & =1.398-0.699x\textrm{ }\\ 1.301x & =1.097\\ x & =0.843. \end{align*}\]
Growth and Decay
Exponential and logarithmic expressions occur in formulae used to model growth and decay in all branches of science.
Example
The number of bacteria present in a sample is given by \(N=800e^{0.2t},\) where \(t\) is the time in seconds.
Find a) the initial number of bacteria and b) the time taken for the bacteria count to reach \(10000\).
- The initial number of bacteria is the count when \(t=0\):
\[\begin{align*} N & =800e^{0.2t}\\ & =800e^{0.2\times0}\\ & =800e^{0}\\ & =800. \end{align*}\]
- To find \(t\) when N\(=10000.\;\)
2 In this solution we use the log law: \[\begin{align*} \ln a^{b} & =b\ln a. \end{align*}\] So that \[\begin{align*} \ln e^{0.2t} & =0.2t\ln e. \end{align*}\]
\[\begin{align*} N & =800e^{0.2t}\\ 10000 & =800e^{0.2t}\\ \frac{10000}{800} & =e^{0.2t}\\ 12.5 & =e^{0.2t}\\ \ln12.5 & =\ln e^{0.2t}\textrm{(use ln when the base is $e)$ }\\ \ln12.5 & =0.2t\ln e\\ \ln12.5 & =0.2t\ (\textrm{remember}\ln e=\log_{e}e=1)\\ t & =\frac{\ln12.5}{0.2}\\ t & =12.6. \end{align*}\]
It takes \(12.6\) sec for the number of bacteria to reach 10000.
Exercises
- Solve for \(x\):
- \(3^{1-x}=27\)
- \(2^{2x-1}=128\)
- \(9^{\frac{1}{x}}=3^{-4}\)
- \(5^{x}=12\)
- \(2^{x-3}=9\)
- \(\frac{1}{2^{x+1}}=4^{x+2}\)
- The decay rate for a radioactive element is given by \(R=400e^{-0.03t}\) where \(t\) is measured in seconds. Find
- the initial decay rate
- the time for decay rate to reduce to half the initial decay rate.
- The charge \(Q\) units on the plate of a condenser \(t\) seconds after it starts to discharge is given by \(Q=Q_{0}10^{-kt.}.\) If the initial charge is \(5076\) units and \(Q=1840\) when \(t=0.5\)sec, find
- the value of k
- the time needed for the charge to fall to \(1000\) units
- the charge after \(2\)sec.
\[\begin{array}{lllllll} 1. & a)\ x=-2 & b)\ x=4 & c)\ x=-1/2 & & & \\ & d)\ x=1.54 & e)\ x=6.17 & f)\ x=-1.67 & & & \\ 2. & i) \,R=400 & ii) \,t=23.1\,s & & & & \\ 3. & i) \,k=0.881 & ii) \,t=0.8\,s & iii) \,Q=87.8 units & & & \\ \end{array}\]
Download this page, Exponential Equations (PDF 109 KB)
What's next... ILS3.1 Simplifying surds
