Equation of a plane in 3D

Just as we can define an equation for a line in three dimensions, we can do the same for an entire plane–that is, we can define an equation that represents a two-dimensional space within a 3D space.

A plane is a subset of three dimensional space. You can think of it as a flat surface that extends infinitely in two directions. It may be defined as:

• the surface that goes through three points; or
• the surface containing a point and having a fixed normal vector.

Cartesian equation of a plane

A Cartesian equation is a way to describe shapes using the \(x\)—\(y\) coordinate system. It is handy for analysing the properties and positions of geometric 2D shapes in 3D space.

Consider the following diagram, which shows a part of a plane.

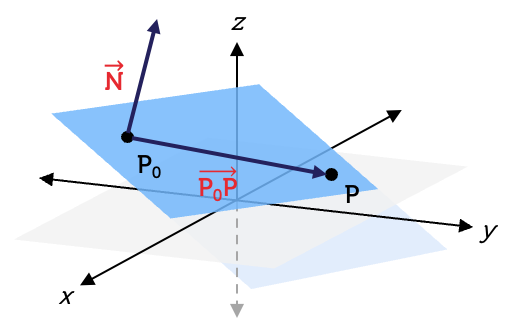
On the plane are two points, \(P(x,y,z)\) and \(P_{0}(x_{0},y_{0},z_{0})\). The equation for the vector extending from \(P_{0}\) to \(P\) is:
\[\overrightarrow{P_{0}P} = (x-x_{0})\hat{i}+(y-y_{0})\hat{j}+(z-z_{0})\hat{k}\]

The diagram also shows a normal vector to the plane—that is, a vector at right angles to the plane—represented by:
\[\overrightarrow{N}=a\hat{i}+b\hat{j}+c\hat{k}\]

where \(a\), \(b\) and \(c\) are constants.
Another normal is given by \(-\overrightarrow{N}=-a\hat{i}-b\hat{j}-c\hat{k}\); this just a vector in the opposite direction of \(\overrightarrow{N}\) and is still at right angles to the plane.

As \(\overrightarrow{N}\) is perpendicular to \(\overrightarrow{P_{0}P}\), their scalar or dot product must equal \(0\). Go back to the page on scalar or dot product to review this concept.

This means \(\overrightarrow{N}\cdot\overrightarrow{P_{0}P}=0\). Written out in full, this is:
\[(a\hat{i}+b\hat{j}+c\hat{k})\cdot((x-x_{0})\hat{i}+(y-y_{0})\hat{j}+(z-z_{0})\hat{k})\]

So:

\[a(x-x_{0})+b(y-y_{0})+c(z-z_{0}) = 0\]

This equation defines the plane in Cartesian coordinates.

We can rearrange the equation by expanding the brackets and moving all of the \(P_{0}\) coordinates to one side and the \(P\) coordinates to the other:
\[\begin{align*} a(x-x_{0})+b(y-y_{0})+c(z-z_{0}) & = 0\\
ax+by+cz & = ax_{0}+by_{0}+cz_{0}\\
& = d
\end{align*}\]

where \(d\) is a constant.

In fact, the general equation of a plane with the normal vector \(\overrightarrow{N}=a\hat{i}+b\hat{j}+c\hat{k}\) is:

\[ax+by+cz = d\]

Some examples of equations representing planes are:

• \(2x-3y+z=6\)
• \(x+y=4\)
• \(z=x-2y+3\).

Parallel planes

There are an infinite number of parallel planes that are perpendicular to a given vector. For instance \(2x-3y+z=6\), \(2x-3y+z=0\), \(2x-3y+z=-1\) and \(2x-3y+z=11\) are all perpendicular to the vector \(2\hat{i}-3\hat{j}+\hat{k}\). However, only one of these will pass through a given point.

Example 1 – finding the equation of a plane

If a plane has the normal vector \(\overrightarrow{N}=\hat{i}+2\hat{j}-5\hat{k}\) and contains the point \((3,4,1)\), determine the equation that represents it.

Substitute the values into the correct formula to find the equation. The normal vector is in the form \(a\hat{i}+b\hat{j}+c\hat{k}\) and the point is \((x_{0},y_{0},z_{0})\).
\[\begin{align*} a(x-x_{0})+b(y-y_{0})+c(z-z_{0}) & = 0\\
1(x-3)+2(y-4)-5(z-1) & = 0\\
x-3+2y-8-5z+5 & = 0\\
x+2y-5z & = 3+8-5\\
x+2y-5z & = 6
\end{align*}\]

You may notice that the coefficients for \(\hat{i}\), \(\hat{j}\) and \(\hat{k}\) for the normal vector \(\overrightarrow{N}\) are the same as the coefficients for \(x\), \(y\) and \(z\) in the equation for the plane.

Exercise – finding the equation of a plane

1. Determine the vectors normal to the following planes.
1. \(2x+3y+7z=13\)
2. \(z=x+3y-9\)
2. Find the equation of the plane that contains the point \((2,3,1)\) and has the normal vector \(4\hat{i}+3\hat{j}-2\hat{k}\).
3. Find the equation of the plane that contains the point \((5,-3,2)\) and has the normal vector \(\hat{i}-9\hat{j}-4\hat{k}\).
4. Find the equation of the plane that contains the point \((1,-1,0)\) and is parallel to the plane \(x-3y+2z=0\).
5. Find the equation of the plane that contains the points \((1,2,3)\), \((2,1,1)\) and \((-3,0,4)\).

Images on this page by RMIT, licensed under CC BY-NC 4.0