Linear graphs
Determining whether two lines intersect can also be done graphically. Use this resource to learn more.
Intersecting lines in 3D
Vectors can be used to determine whether two lines in 3D cross each other (or intersect), and identify the point at which they intersect. This is used in a variety of STEM disciplines, including detection of collisions between objects in robotics and modelling complex structures in computer graphics and game development. Use this resource to learn more.
To find the point of intersection of two lines in 3D space, it is best to have both equations in parametric form, with different parameters for each line. For example, the set of equations for the first line may be written in terms of \(t\) while the other for second line is written in terms of \(s\).
If the lines intersect, there must be values of \(s\) and \(t\) that give the same point on each of the lines. If this is not the case, the lines do not intersect.
The basic approach is:
- Write each line in parametric form.
- Solve the simultaneous equations for the parameters.
- If a solution exists, the lines intersect. If not, they don’t intersect.
Let's look at some examples.
Example 1 – determining the point of intersection between two lines
Find the point of intersection of the two lines \(L_{1}\) and \(L_{2}\) where \(L_{1}\) is the line represented by the equation \(\dfrac{x-5}{1}=\dfrac{y-1}{-1}=\dfrac{z-8}{-3}\) and \(L_{2}\) is the line represented by \(x=1+2s\), \(y=-4+s\) and \(z=8-2s\).
The first step is to write each line in parametric form. Line \(L_{2}\) is already in parametric form:
\[x=1+2s\] \[y=-4+s\] \[z=8-2s\]
For line \(L_{1}\), we let each component equal to another parameter that is not \(s\). Let's go with \(t\).
\[\frac{x-5}{1}=t\] \[\frac{y-1}{-1}=t\] \[\frac{z-8}{-3}=t\]
Rearranging them so that they are written with \(x\), \(y\) and \(z\) as the subjects:
\[x=5+t\] \[y=1-t\] \[z=8-3t\]
To find the point of intersection of lines \(L_{1}\) and \(L_{2}\), we must find a point \(P\) that lies on both lines.
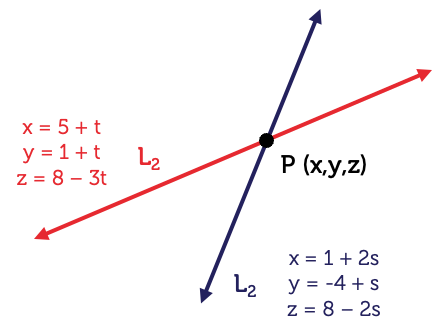
At the point of intersection, the coordinates for \(L_{1}\) will equal the coordinates for \(L_{2}\). This means there exist values of \(s\) and \(t\) such that the \(x,\) \(y\) and \(z\) coordinates of the two lines are equal. To work this out, we equate the \(x\), \(y\) and \(z\) coordinates.
For \(x\):
\[\begin{align*} 5+t & = 1+2s\\
4 & = 2s-t
\end{align*}\]
For \(y\):
\[\begin{align*} 1-t & = -4+s\\
5 & = s+t
\end{align*}\]
For \(z\):
\[\begin{align*} 8-3t & = 8-2s\\
0 & = 3t-2s
\end{align*}\]
To solve for \(s\) and \(t\), we can add the \(x\) and \(y\) equations:
\[\begin{align*} 4+5 & = 2s-t+s+t\\
9 & = 3s\\
\frac{9}{3} & = s\\
3 & = s
\end{align*}\]
We can substitute \(s=3\) into another equation to find \(t\). Let's start with the equation for \(x\):
\[\begin{align*} 4 & = 2s-t\\
4 & = 2(3)-t\\
4 & = 6-t\\
t & = 2
\end{align*}\]
The solution \(s=3\) and \(t=2\) may not necessary satisfy all of the equations, so you must check all of them. For the \(y\) equation:
\[\begin{align*} \textrm{RHS} & = s+t\\
& = 3+2\\
& = 5\\
& = \textrm{LHS}
\end{align*}\]
And finally, the \(z\) equation:
\[\begin{align*} \textrm{RHS} & = 3t-2s\\
& = 3(2)-2(3)\\
& = 0\\
& = \textrm{LHS}
\end{align*}\]
\(s=3\) and \(t=2\) satisfy all three equations, so it is the solution. To find the point of intersection, we substitute the \(s\) value into the equations for \(L_{2}\) and the \(t\) value into the equations for \(L_{1}\).
For \(L_{1}\):
\[\begin{align*} x & = 5+t\\
& = 5+2\\
& = 7
\end{align*}\] \[\begin{align*} y & = 1-t\\
& = 1-2\\
& = -1
\end{align*}\] \[\begin{align*} z & = 8-3t\\
& = 8-3(2)\\
& = 2
\end{align*}\]
For \(L_{2}\):
\[\begin{align*} x & = 1+2s\\
& = 1+2(3)\\
& = 7
\end{align*}\] \[\begin{align*} y & = -4+s\\
& = -4+3\\
& = -1
\end{align*}\] \[\begin{align*} z & = 8-2s\\
& = 8-2(3)\\
& = 2
\end{align*}\]
You can see that these give the same coordinates: \((7,-1,2)\). Here, it doesn't matter which set of equations you substitute the values into, as it is the point of intersection that both lines share.
Determine whether the lines \(L_{1}\): \(x=s\), \(y=-4+s\), \(z=8-2s\) and
\(L_{2}\): \(x=2+2t\), \(y=-1+t\), \(z=3-2t\) intersect.
\(L_{2}\): \(x=2+2t\), \(y=-1+t\), \(z=3-2t\) intersect.
The lines are already shown in parametric form, so we just need to equate the coordinates.
For \(x\):
\[\begin{align*} s & = 2+2t\\
s-2t & = 2
\end{align*}\]
For \(y\):
\[\begin{align*} -4+s=-1+t\\
s-t & = 3
\end{align*}\]
For \(z\):
\[\begin{align*} 8-2s & = 3-2t\\
-2s+2t & = -5
\end{align*}\]
Now, we can solve the simultaneous equations. We can subtract the \(x\) equation from the \(y\) equation:
\[\begin{align*} s-t-(s-2t) & = 3-2\\
t & = 1
\end{align*}\]
We can substitute \(t=1\) into another equation to find \(s\). Let's start with the equation for \(x\):
\[\begin{align*} s & = 2+2t\\
& = 2+2(1)\\
& = 4
\end{align*}\]
This gives us \(t=1\) and \(s=4\), but remember, we need to check that the solution also works with the other equations.
For the \(y\) equation:
\[\begin{align*} \textrm{LHS} & s-t\\
& = 4-1\\
& = 3\\
& = \textrm{RHS}
\end{align*}\]
This works. Let's try the \(z\) equation:
\[\begin{align*} \textrm{LHS} & = -2s+2t\\
& = -2(4)+2(1)\\
& = -8+2\\
& = -6\\
& \neq \textrm{RHS}
\end{align*}\]
Since the solution satisfies the \(x\) and \(y\) equations but not the \(z\) equation, we conclude that there is no solution for \(t\) and \(s\), and the lines do not intersect. Instead, we say that the lines are skew.
Exercise – determining the point of intersection between two lines
- Find the point of intersection of the lines \(x=2t+2\), \(y=2t+3\), \(z=t+3\) and \(\dfrac{x+2}{2}=\dfrac{y-2}{-1}=\dfrac{z}{2}\).
- \((0,1,2)\)
Images on this page by RMIT, licensed under CC BY-NC 4.0
