Vector or cross product

The vector product is another way to multiply two vectors. Just like scalar products, vector products have many broad applications, such as in electrical engineering, quantum physics, software development, game programming and statistics. Use this resource to learn more.

The vector product is a vector resulting from multiplying the magnitudes (size) of two vectors. Compare this to the scalar or dot product, which gives a scalar.

The magnitudes are found using matrices and determinants, so make sure you are confident with these before you continue.

Let's consider the unit vectors \(\hat{i}\), \(\hat{j}\) and \(\hat{k}\) which are in the \(x\), \(y\) and \(z\) directions, respectively. We can write these as:
\[\begin{align*} \hat{i} & = \hat{i}+0\hat{j}+0\hat{k}\\
& = (1,0,0)
\end{align*}\] \[\begin{align*} \hat{j} & = 0\hat{i}+\hat{j}+0\hat{k}\\
& = (0,1,0)
\end{align*}\] \[\begin{align*} \hat{k} & = 0\hat{i}+0\hat{j}+\hat{k}\\
& = (0,0,1)
\end{align*}\] They give us two vectors:
\[\vec{a} = a_{1}\hat{i}+a_{2}\hat{j}+a_{3}\hat{k}\] \[\vec{b} = b_{1}\hat{i}+b_{2}\hat{j}+b_{3}\hat{k}\] Geometrically, the vector product is found using: \[\vec{a}\times\vec{b}=\left|\vec{a}\right|\left|\vec{b}\right|\sin(\theta)\hat{n}\] where \(\hat{n}\) is a unit vector perpendicular to both \(\vec{a}\) and \(\vec{b}\) and \(\theta\) is the angle between the vectors.

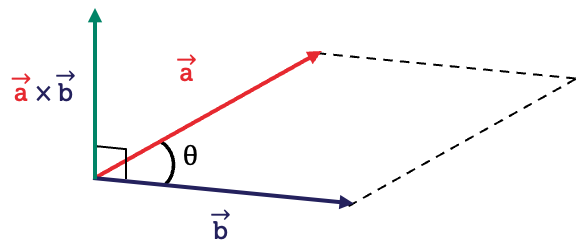
This helps us understand the magnitude and direction of the vector, but in practice, we use the component form:

\[\begin{align*} \vec{a}\times\vec{b} & = \left| \begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\
a_{1} & a_{2} & a_{3}\\
b_{1} & b_{2} & b_{3}
\end{array} \right| \\
& = \hat{i}\left| \begin{array}{cc} a_{2} & a_{3}\\
b_{3} & b_{3}
\end{array} \right| - \hat{j}\left| \begin{array}{cc} a_{1} & a_{3}\\
b_{1} & b_{3}
\end{array} \right| + \hat{k}\left| \begin{array}{cc} a_{1} & a_{2}\\
b_{1} & b_{2}
\end{array} \right| \\
& = \hat{i}(a_{2}b_{3}-b_{2}a_{3})-\hat{j}(a_{1}b_{3}-b_{1}a_{3})+\hat{k}(a_{1}b_{2}-b_{1}a_{2})
\end{align*}\]

The vector product is also commonly referred to as the cross product as a cross (or multiplication symbol) is used between the two vectors being multiplied.

Keep in mind that the vertical delimiters (\(\left| \right|)\) here denote the determinant of the matrix, and not the magnitude of the vector.

Properties of the vector or cross product

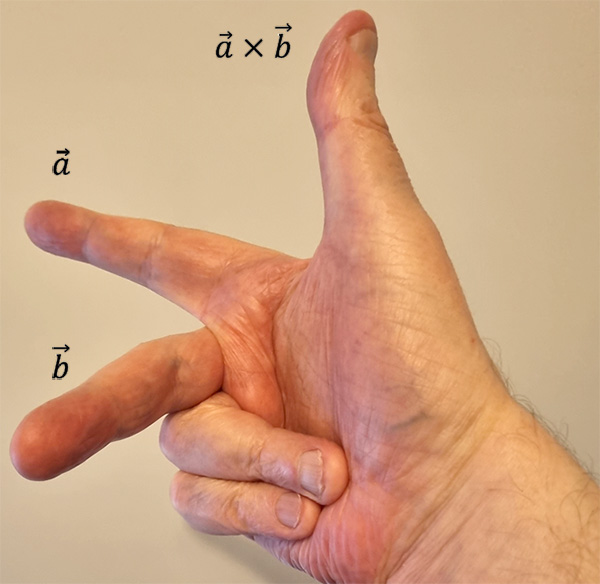
There are some key characteristics of vector products that are handy to remember.

1. If \(\vec{a}\) is parallel to \(\vec{b}\), then \(\vec{a}\times\vec{b}=\vec{0}\) as
   \[\begin{align*} \vec{a}\times\vec{b} & = \left|\vec{a}\right|\left|\vec{b}\right|\sin(0)\hat{n}\\
   & = \vec{0} \end{align*}\]
   as \(\sin(0)=0\). Since the vector product is a vector, we should write the answer as the zero vector, \(\vec{0}\), instead of the number \(0\).
2. The order in which you take the cross product is important. In fact, \(\vec{a}\times\vec{b}=-\vec{b}\times\vec{a}\).
3. The direction of \(\vec{a}\times\vec{b}\) is perpendicular (\(90^{\circ})\) to the plane in which both \(\vec{a}\) and \(\vec{b}\) sit on. We can visualise this as the direction in which your thumb would point if the fingers of your right hand are curled from \(\vec{a}\) to \(\vec{b}\).
   

   

   This is called the right hand rule.

Example 1 – calculating the vector product

Find \(\vec{a}\times\vec{b}\) if \(\vec{a}=2\vec{i}+3\vec{j}+\vec{k}\) and \(\vec{b}=5\vec{j}+3\vec{k}\).

Vectors must first be written in matrix form. We place the variables—in this case, the unit vectors—in the first row. In the second and third rows of the matrix, we put the corresponding coefficients for the vectors \(\vec{a}\) and \(\vec{b}\), respectively.

This gives us the matrix:
\[\begin{align*} \vec{a}\times\vec{b} & = \left| \begin{array}{ccc} \hat{i} & \hat{j} & \hat{k}\\
2 & 3 & 1\\
0 & 5 & 3
\end{array} \right|
\end{align*}\]
To find the vector or cross product, we simply find the determinant of the matrix.

Cartesian unit vectors

If we just look at the cartesian unit vectors—that is, the unit vectors that lie along the \(x\)-, \(y\)- and \(z\)-axes—there are a few rules that are helpful to remember.

Again, we will let \(\hat{i}\), \(\hat{j}\) and \(\hat{k}\) be unit vectors in the \(x\), \(y\) and \(z\) directions, respectively. The rules are:

1. \(\hat{i}\times\hat{j}=\hat{k}\)
2. \(\hat{j}\times\hat{k}=\hat{i}\)
3. \(\hat{k}\times\hat{i}=\hat{j}\)
4. \(\hat{i}\times\hat{k}=-\hat{j}\)
5. \(\hat{k}\times\hat{j}=-\hat{i}\)
6. \(\hat{j}\times\hat{i}=-\hat{k}\)

These rules make finding the vector product more efficient as we can derive answers without having to complete calculations.

Example 4 – calculating the vector product

Find \(\hat{i}\times\hat{k}\).

We can write these are vectors first.
\[\hat{i}=\hat{i}+0\hat{j}+0\hat{k}\] \[\hat{k}=0\hat{i}+0\hat{j}+\hat{k}\]
Now, let's find the vector product.

Exercise – calculating the vector product

1. Calculate the following.
1. \(\hat{j}\times\hat{k}\)
2. \(\hat{i}\times4\hat{i}\)
3. \((2\hat{i}+3\hat{j}-\hat{k})\times(3\hat{j}+2\hat{k})\)
4. \(3\hat{j}\times5\hat{i}\)
5. \((\hat{i}-3\hat{j}+\hat{k})\times(2\hat{i}+\hat{j}-\hat{k})\)
2. Find a unit vector perpendicular to both \((\vec{i}-\vec{k})\) and \((\vec{i}+3\vec{j}-2\vec{k})\).

Images on this page by RMIT, licensed under CC BY-NC 4.0